LCS(Longest Common Subsequence), 최장 공통 부분 수열을 학습하자.

JUNHO CHOI·2023년 12월 26일

알고리즘 공부

목록 보기

3/3

1. 어떤 알고리즘인가?

입력으로 주어진 2개 이상의 문자열에 대해 LCS(Longest Common Subsequence, 최장 공통 부분 수열)을 구하는 알고리즘을 의미한다.

부분 수열?
원래 수열의 일부 항을 순서를 고려해서 나열했을 때 얻을 수 있는 수열
ex) 문자열 "ABCDEF"가 있을 때 {'A', 'B', 'C', 'D', 'E', 'F'} 와 같은 수열을 얻을 수 있고, {'A', 'C', 'F'}와 같은 부분 수열이 있을 수 있다.

2. 문제 정의

두 문자열 A, B가 주어졌을 때, LCS의 길이를 구하라

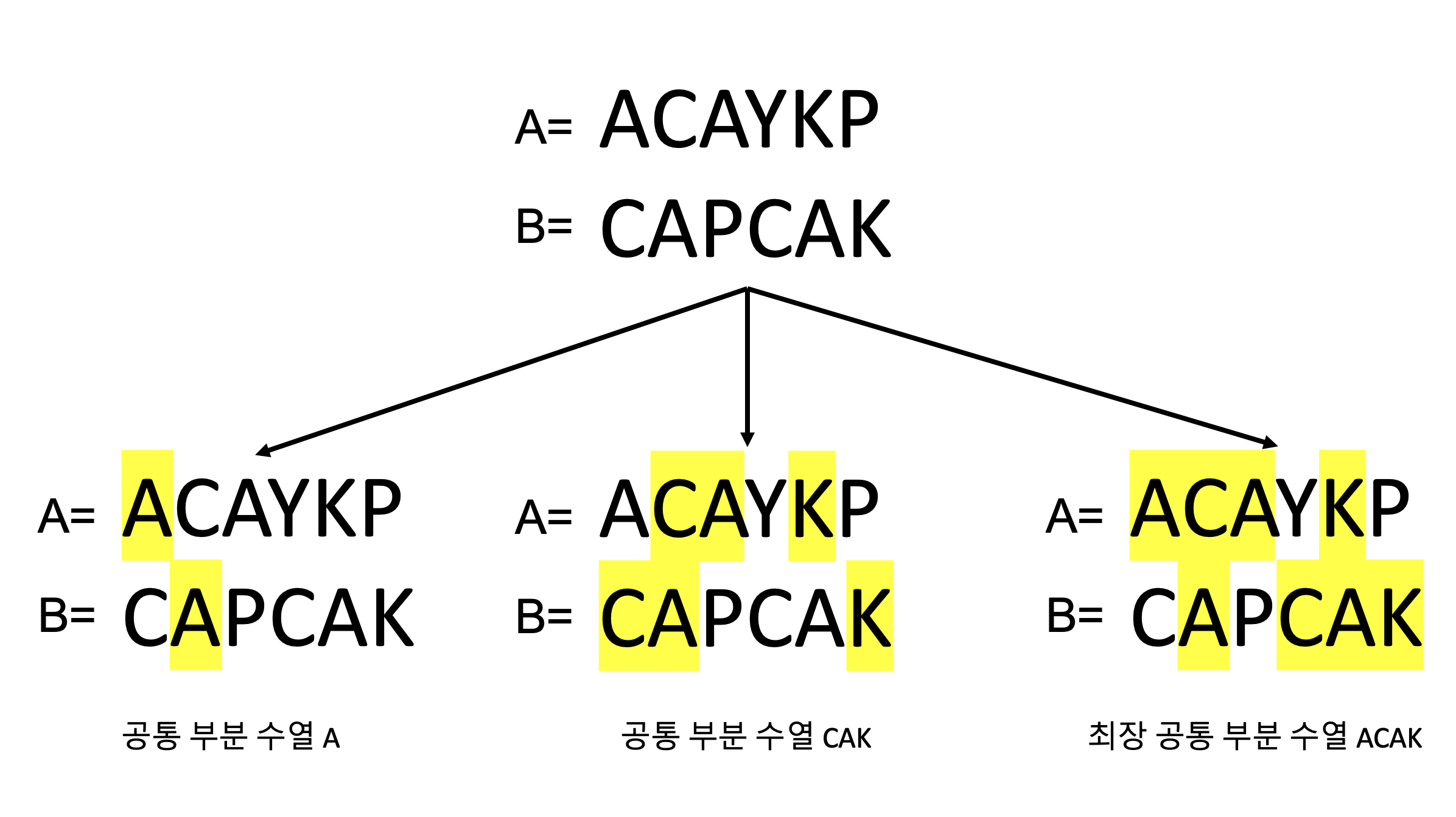
예를 들어 다음과 같이 두 문자열 A="ACAYKP"와 B="CAPCAK"가 있다고 하면
여러 개의 공통 부분 수열이 있을 수 있고 LCS은 "ACAK"이며 이때 길이는 4이다.

3. 솔루션 스케치

해당 문제를 풀기 위한 알고리즘을 어떻게 구상할 수 있을까?
1. 가능한 모든 공통 부분 수열을 탐색해서 LCS를 찾기 위해 재귀를 사용한다.
2. 최적화가 가능한 부분 문제 구조를 갖으며 중복되는 부분 문제가 많다. 따라서 DP를 사용해 효율적인 알고리즘을 작성한다.

4. 솔루션 도출

4-1. 재귀를 이용한 풀이

두 문자열 A, B가 있고 각각 문자열 길이 m, n이라고 하자.
A[0, m-1]는 0번 문자부터 m-1번 문자까지의 부분 문자열을 표현한다고 하자. (0's based indexing)
LCS(A, B, m, n)은 문자열 A의 부분 문자열 A[0, m-1]과 문자열 B의 부분 문자열 B[0, n-1]의 LCS라고 부분 문제를 정의하자.

A[0, m-1]과 B[0, n-1] 의 LCS를 구하기 위해서
1. 각각 마지막 문자의 공통 여부를 판단하고
2. 만약 공통 문자라면 LCS에 +1를 해준다.
3. 아니라면 A[0, m-2]와 B[0, n-1]을 다시 비교하거나, A[0, m-1]와 B[0, n-2]를 비교해서 반환되는 길이가 더 큰 값을 선택한다.
4. 부분 문자열의 길이가 0이 될 때까지 재귀 호출을 하게 된다.

탐색 공간 트리

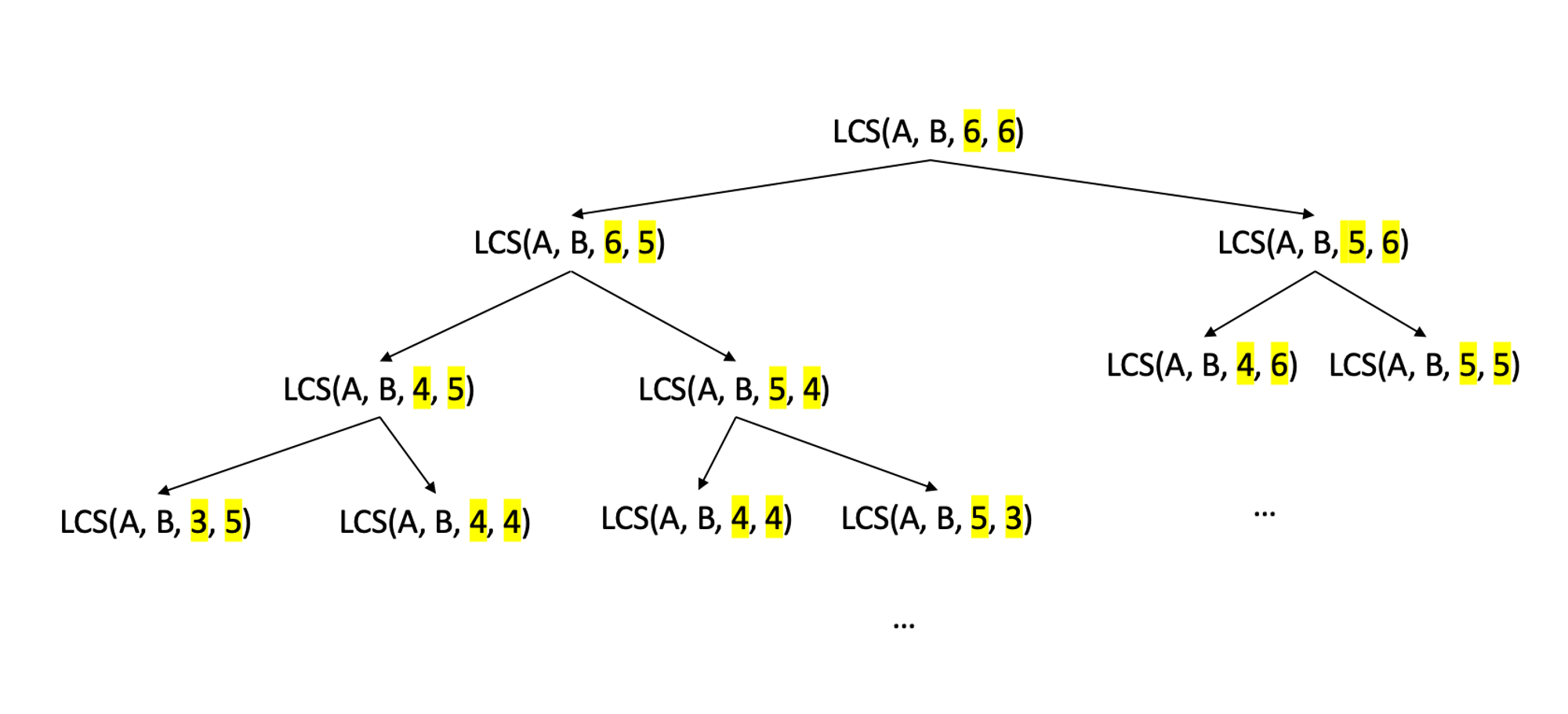
시간 복잡도 계산
해당 풀이의 경우 하나의 상태를 표현하는 재귀함수에서 다음 상태로 전이할 때 두 번의 재귀함수 호출이 일어난다. 또한 부분 문자열을 하나씩 줄여가며 호출하므로 시간 복잡도는 다음과 같다.

O(2^{MN})

코드

int lcs(String a, String b, int m, int n) {
	if(m == 0 || n == 0) {
    	return 0;
        }
        
    // 마지막 문자가 서로 공통될 때 
    if(a.charAt(m - 1) == b.charAt(n - 1)) {
    	return 1 + lcs(a, b, m - 1, n - 1);
    } else {
    	return Math.max(lcs(a, b, m, n - 1), lcs(a, b, m - 1, n));  
    }
}

4-2. DP를 이용한 최적화

앞서 재귀를 이용한 풀이에서 최적화가 가능한 부분 문제 구조를 갖고 있었음을 확인할 수 있었다. 예를 들면 LCS(A, B, m, n)의 결과는 LCS(A, B, m-1, n-1)의 결과를 먼저 해결할 필요가 있는 구조였다.
또한 탐색 공간 트리에서 중복적으로 호출되는 재귀함수가 있음을 확인할 수 있었다.

하향식(Top-down) 방법을 통한 풀이

이미 해결한 부분 해를 기록하기 위한 배열을 생성하고 초기화하는 코드 추가

int[][] dp = new int[m + 1][n + 1];
final int NOT_SOLVED = -1;
for(int i = 0; i <= m; i++) {
	Arrays.fill(dp[0], NOT_SOLVED);
}

탐색 과정 중 이미 부분해를 구한 경우라면 재귀호출을 종료하는 코드를 추가

int lcs(String a, String b, int m, int n) {
    if(m == 0 || n == 0) {
        return 0;
    }

    if(dp[m][n] != NOT_VISITED) {
        return dp[m][n];
    }

    // 마지막 문자가 서로 공통될 때
    if(a.charAt(m - 1) == b.charAt(n - 1)) {
        dp[m][n] = 1 + lcs(a, b, m - 1, n - 1);
    } else {
        dp[m][n] = Math.max(lcs(a, b, m, n - 1), lcs(a, b, m - 1, n));
    }

    return dp[m][n];
}

상향식(Bottom-up) 방법을 통한 풀이

2차원 배열 dp[][]의 행과 열의 인덱스 i, j에 대해서 두 문자열 A, B의 i번째, j번째 문자로 맵핑한다.
예를 들어 A="ACAYKP", B="CAPCAK"라고 하면 다음과 같은 2차원 배열을 고려할 수 있다.
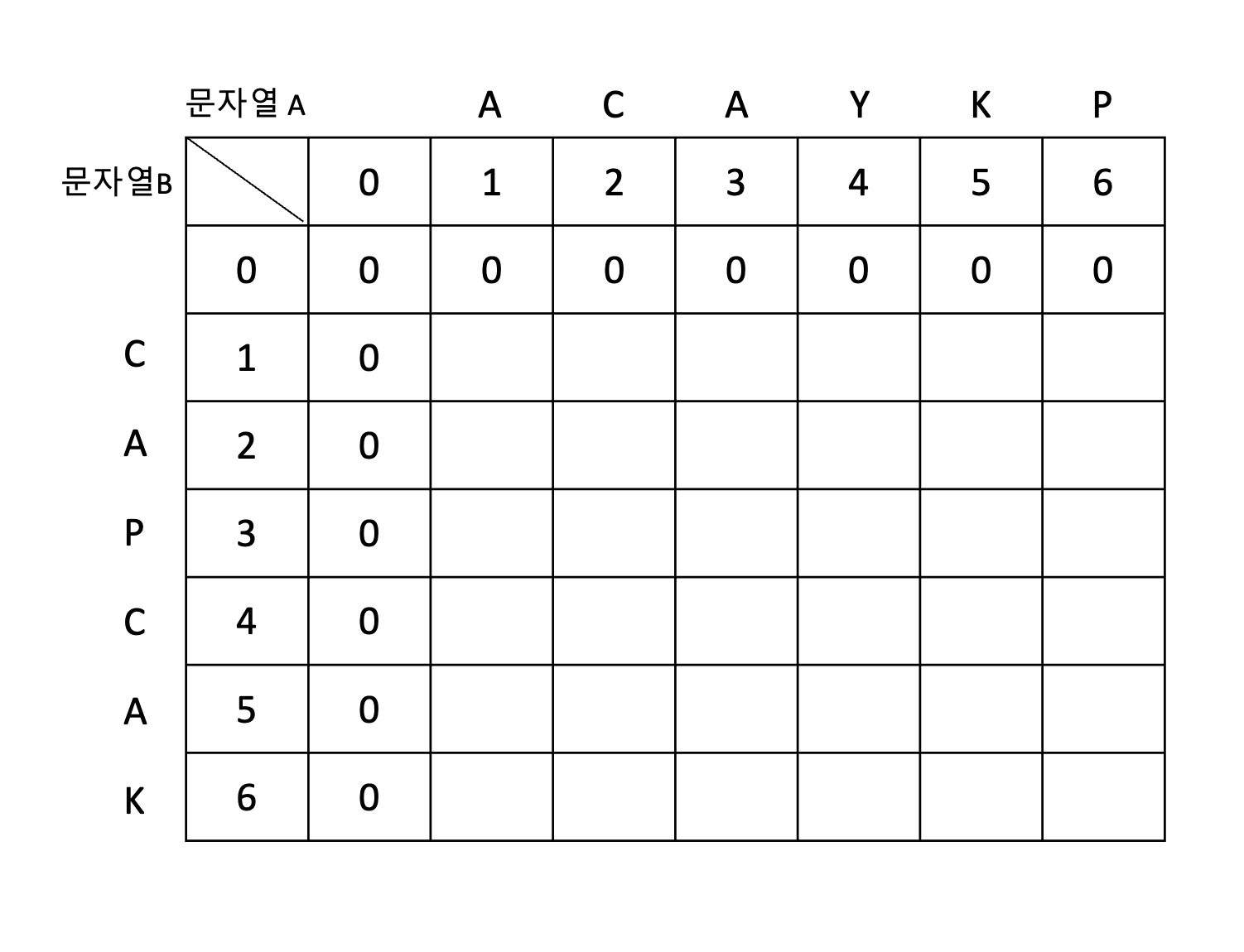행 성분은 문자열 B, 열 성분은 문자열 A의 각 문자를 인덱싱(1's based indexing)

어떻게 LCS를 구할까?

먼저 i=1, j=1번 요소부터 모든 배열의 요소를 계산한다.
그러면서 A[i]와 B[j]의 문자가 서로 일치하면 LCS 길이를 증가시켜주고
아니라면 부분 문자열 A[1, i-1], B[1, j]에 대한 LCS와 부분 문자열A[1, i], B[1, j-1]에 대한 LCS 중 최대값을 기록하면서 반복문을 통해 채워간다.
최종적으로 D[m][n]을 전체 문자열에 대한 LCS를 반환한다.

자바 코드

for (int i = 1; i <= m; i++) {
    for (int j = 1; j <= n; j++) {
        if (A[i] == B[j]) {
            D[i][j] = D[i - 1][j - 1] + 1;
            continue;
        }
        D[i][j] = Math.max(D[i - 1][j], D[i][j - 1]);
    }
}
int answer = D[m][n];
System.out.println(answer);