📌 서론.
코딩테스트를 준비하다보면 많은 강의들이 ‘시간복잡도를 유의하고 문제를 풀어라’ 라는 말들을 접해본 적이 많았을 것이다.
제한사항에서
길이가 1,000,000 이하 인 문자열 배열이라는 제한사항도 많이 접해봤을 것이다. 필자도 이러한 배열에서 이중 for문을 돌리다가 실패한 경험을 많이 했었다.
바킹독의 해당 강의에서는 이러한 제한 사항이 주어졌을 때, 이러한 제한 사항에 대해서 시간복잡도, 공간복잡도를 어떻게 연결지어 생각하고, 접근할 것인지에 대한 테크닉을 배웠다.
📝 시간복잡도.
시간복잡도란??
- 정의 :
입력의 크기와 문제를 해결하는데 걸리는시간의 상관관계
Big-O 표기법
- 주어진 값이 가장 큰 대표항만 남겨서 나타내는 방법
| Big-O 표기법 | 예시 |
|---|---|
| O(N) | 5N + 3, N+10lgN |
| O(N^2) | N^2 + 2N + 4, 6N^2 + 20N + 10lgN |
| O(NlgN) | NlgN + 30N + 6 |
| O(1) | 45, 1, 46 |
잠깐! 가장 큰 대표항만 남겨서 나타내는 방법이라면
20N + 10lgN같은 경우N이 큰지lgN이 큰지 어떻게 알아?
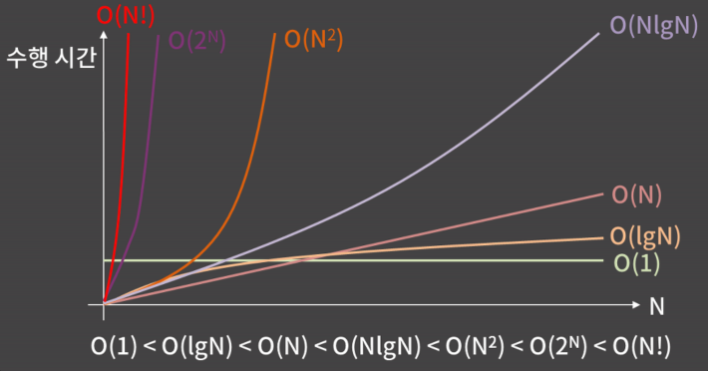
해당 그래프를 보자. N이 충분히 클 경우를 상정하고 Big-O 표기법을 사용하는 것이기에 20N + 10lgN 의 경우 표기는 O(N) 이 될것이다!
너가 보여준 그래프대로라면 N(데이터의 양)이 10 이내인 경우라면 O(1) 의 수행시간이보다 O(N!) 의 수행시간 보다 작잖아!
그렇다. 그렇기에 코테 문제에서 보여주는 제한사항에 따른 허용 시간복잡도를 확인하는것이 유의미해지는 것이다!
| N의 크기 | 허용 시간 복잡도 |
|---|---|
| N ≤ 11 | O(N!) |
| N ≤ 25 | O(2N) |
| N < 100 | O(N^4) |
| N ≤ 500 | O(N^3) |
| N ≤ 3,000 | O(N^2IgN) |
| N ≤ 5,000 | O(N^2) |
| N ≤ 1,000,000 | O(NIgN) |
| N ≤ 10,000,000 | O(N) |
| 그 이상 | O(lgN), O(1) |
만약 제한 사항에 N의 크기가 1,000,000 개가 주어졌다면 해당 제한 사항의 시간복잡도를 지키려면 O(NlogN) 보다 빠른 알고리즘을 써야겠구나~ 하고 생각하면 된다.
물론 해당 표가 절대적인 기준은 아니다. N이 10,000인데도 O(N²)이 통과될 수 있고, 반대로 복잡한 연산이 많은 경우 N이 1,000,000인데도 O(NlgN)이 통과되지 않을 수도 있다.
하지만 해당 표를 인지하고 있다면 주어진 문제를 보고 풀이를 떠올린 후에 무턱대로 그걸 짜보는 것이 아니라 제한 시간 내로 통과할 수 있는지 미리 생각해보고 시간을 아낄 수 있는 시간초과될 알고리즘을 쳐낼 수 있는 힘을 기를 수 있다!
📝 공간복잡도.
- 정의 :
입력의 크기와 문제를 해결하는데 걸리는공간의 상관관계 - 코테에서는 보통 공간복잡도보다 시간복잡도 때문에 문제를 틀리는 경험을 많이 하게된다.
- 제한사항에 메모리 제한이
512MB라면 1.2억개의 인수를 갖는 int 배열을 가질 수 있다는 걸 기억하면 좋음
📝 정수 자료형
Java의 경우 각 자료형당 차지하는 크기는 다음과 같다.
| 데이터 형식 | 크기 | 허용 범위 | 개수 |
|---|---|---|---|
| boolean | 1 바이트 | true, false | 2^7-1(=127) |
| char | 2 바이트 | 유니코드 문자 | 2^15-1(=32767) |
| byte | 1 바이트 | -128 ~ 127 | 2^7-1(=127) |
| short | 2 바이트 | -32,768 ~ 32,767 | 2^15-1(=32767) |
| int | 4 바이트 | -2,147,483,648 ~ 2,147,483,647 | 2^31-1(≈2.1 * 10^9) |
| long | 8 바이트 | -9,223,372,036,854,775,808 ~ 9,223,372,036,854,775,807 | 2^63-1(≈9.2*10^18) |
| float | 4 바이트 | ±(1.40 × 10^-45 ~ 3.40 × 10^38) | 2^31-1(≈2.1 * 10^9) |
| double | 8 바이트 | +(4.94 x 10^-324 ~ 1.79 × 10^308) | 2^63-1(≈9.2*10^18) |
먄약 80번째 피보나치 수 같이 int 자료형의 표현할 수 있는 범위를 벗어나면 long 자료형을 사용해야한다!
📝 실수 자료형
실수의 저장과 연산에서 오차가 발생할 수 있음을 인지할 것.
실수의 자료형을 다룰때 알고있어야 하는 점은 실수의 저장과 연산 과정에서 반드시 오차가 발생할 수 있다는 것이다.
0.1+0.1+0.1이 0.3과 다르게 나오는 이유는 2진수 기준으로 무한 소수인 0.1을 유한한 크기의 fraction field에 저장하려고 할 때 발생하는 오차 때문!
fraction field 는 float은 앞 23 bit, double은 앞 52 bit까지만 저장 가능
| 데이터 형식 | 크기 | 허용 범위 | 개수 | 유효숫자 |
|---|---|---|---|---|
| float | 4 바이트 | ±(1.40 × 10^-45 ~ 3.40 × 10^38) | 2^31-1(≈2.1 * 10^9) | 6자리 |
| double | 8 바이트 | +(4.94 x 10^-324 ~ 1.79 × 10^308) | 2^63-1(≈9.2*10^18) | 15자리 |
→ float은 상대 오차 10^(-6)까지 안전하고 double은 10^(-15)까지 안전
실수 자료형이 필요한 문제에서는
절대/상대 오차를 허용한다는 단서가 없다면
열에 아홉은 실수를 안쓰고 모든 연산을 정수에서 해결할 수 있는 문제!
double 자료형에 long 범위의 정수를 담으면 안된다는 걸 인지할 것.
double은 유효숫자가 15자리인데 long 은 최대 19자리니까 10^18+1과 10^18을 구분할 수가 없고 그냥 같은 값이 저장됨!
단! int는 최대 21억이기 때문에 double에 담아도 오차가 생기지 않음
실수를 비교할 때는 등호를 사용 금지!
첫번째 이야기와 같은 이야기!
두 실수가 같은지 알고 싶을 때에는 둘의 차이가 아주 작은 값, 대략 10-12 이하면 동일하다고 처리를 하는게 안전
🎯 결론.
이상으로 코딩테스트를 치루기 전 알고있어야 하는 상식들을 알아보았다.
코테를 풀때 시간복잡도를 먼저 생각해두라는 말을 들은 적이 자주 있었는데 허용 시간 복잡도를 잘 알고있다면 필요한 알고리즘들을 추려서 도전할 수 있기에 정말정말 유용하다는 생각을 했다잉
