문제

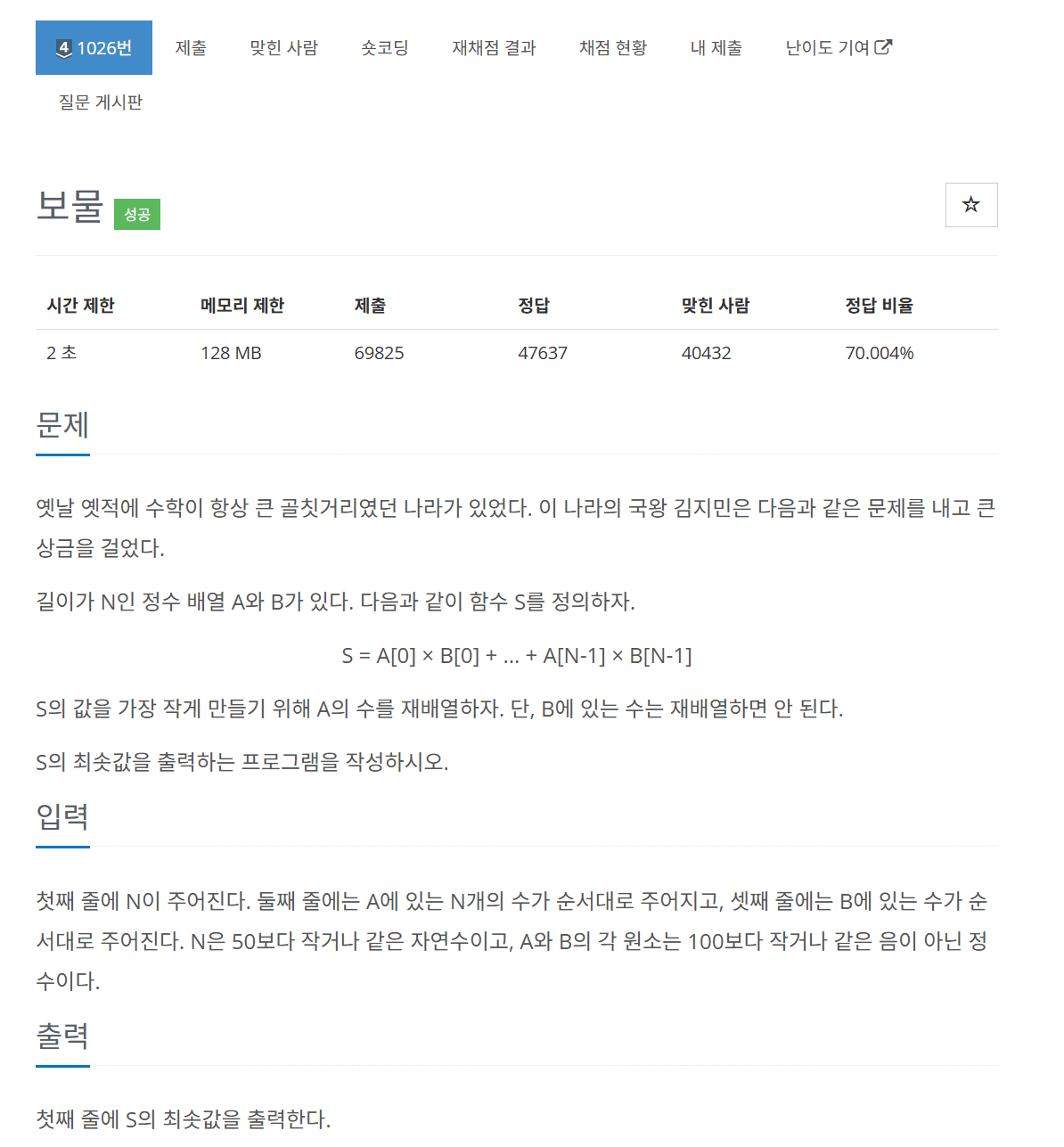
문제 이해

이 문제를 처음 봤을 때는 순열과 브루트포스를 쓰면 풀 수 있다고 생각했다. 하지만 N이 50까지라서 순열을 만드는 것만해도 50!이다. 엄청나게 큰 수라서 브루트포스로는 안정적으로 풀 수가 없다. 실제로 시간초과 판정 받았다. 그래서 이 문제는 그리디로 풀어야 한다. 두개의 배열을 하나는 오름차순, 나머지는 내림차순으로 정렬해서 계산하면 된다. 문제에서는 B배열을 재배열하지 말라고 했지만, 어차피 A배열을 순열로 만들어서 바꾸다보면 그 조합으로 연산을 하는 경우도 있다.

일단 그렇게 해서 문제가 풀린다면, 하나는 오름차순 하나는 내림차순으로 만들어서 계산하는 로직이 정답이라는 걸 알 수 있다.

B를 재배열하지 말라고 했지만, 결국 재배열해도 상관없다는 점에서 이 문제가 그리디하다고 생각이 든다.

시간초과 코드

# 백준 1026번 보물

# 순열 기능 Import
from itertools import permutations

# N 입력
N = int(input())

# a, b 각 배열 입력력
a = list(map(int, input().split()))
b = list(map(int, input().split()))

INF = 1e12
min_sum = INF

for arr in permutations(a, N):

    total_sum = 0
    for i in range(N):
        total_sum += arr[i]*b[i]

    if min_sum > total_sum:
        min_sum = total_sum
    
print(min_sum)

정답 코드

# 백준 1026번 보물

# 순열 기능 Import
from itertools import permutations

# N 입력
N = int(input())

# a, b 각 배열 입력력
a = list(map(int, input().split()))
b = list(map(int, input().split()))

a = sorted(a)
b = sorted(b, reverse=True)

sum = 0
for i in range(N):
    sum += a[i]*b[i]

print(sum)