문제

문제 이해

재귀함수 카테고리의 첫 문제이다.
재귀 함수는 두가지로 분류 할 수 있다. Basecase와 Recursioncase이다. Basecase는 재귀 호출의 마지막 스탑을 해줄 부분이다. 이번 문제 같은 경우는 N번에서 계속 재호출되면서 N이 1, 0이 될땐 따로 값이 정해져 있기 때문에 이를 이용해서 Basecase를 만든다. Recursioncase는 재호출 하는 부분이다.

보통 식으로 나타낼 수 있으면 재귀 형태를 만들 수 있다.
Fn = Fn-1 + Fn-2 (n ≥ 2)
식이 위와 같다면 Fn을 찾기 위해서는 return을 Fn-1 + Fn-2로 재호출하면 된다. N이 계속 감소하다가 0이나 1이 되면 값이 차례대로 올라가서 반환된다.

코드

# 백준 10870번 피보나치 수 5

# 재귀 깊이 확장
import sys
sys.setrecursionlimit(10**6)

# Define Function Fibonacci
def Fibonacci(N): 
    # Base case
    if N == 0: # 가장 마지막 수가 0이니까
        return N # N은 0 즉, 0을 리턴
    elif N == 1:
        return N # N은 1 즉, 1을 리턴
        
    # Recursive case  
    return Fibonacci(N-1) + Fibonacci(N-2)

# 0. 입력
N = int(input())

# 1. Excute Fibonacci Function
print(Fibonacci(N))

이렇게 문제를 풀면 같은 값읗 중복으로 여러번 구하는 경우가 많아진다.

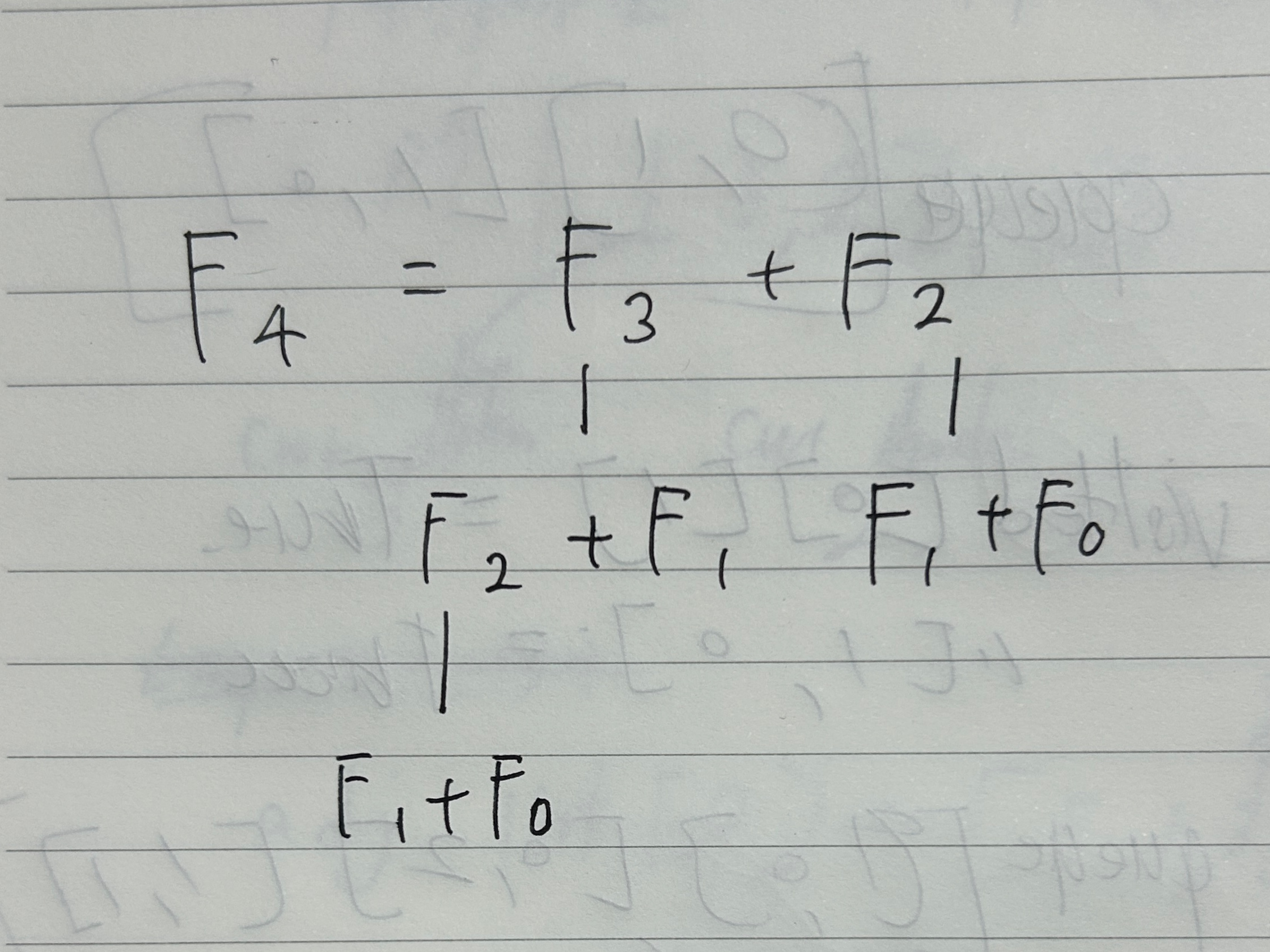
그림처럼 F4를 구하려고 하면 F2가 두번이나 나오지만 다 따로 계산을 해야한다. N의 값이 작아서 중복이 적지만 값이 커지면 그만큼 중복도 많아진다.

그래서 메모이제이션이라고, 이미 구했던 값은 저장해서 쓸 수 있게 하는 방법이 있다.

메모이제이션 사용 코드

# 백준 10870번 피보나치 수 5

# 재귀 깊이 확장
import sys
sys.setrecursionlimit(10**6)

# Define Function Fibonacci
def Fibonacci(x):
    global lst

    if lst[x] != -1: # 값이 이미 들어가 있으면 그 값을 리턴
        return lst[x]

    lst[x] = Fibonacci(x-1) + Fibonacci(x-2)
    return lst[x] 

# 0. 입력
N = int(input())

# -1로 초기화 하는 이유는 안 나올만한 값이기 때문문
lst = [-1] * (N+2) # N+2인 이유는 2개의 값을 미리 지정하기 때문, N+1일때 N=0이면 lst[1]에 접근하면 인덱스 오류가남남
lst[0] = 0
lst[1] = 1
# 1. Excute Fibonacci Function
print(Fibonacci(N))

이런 방식으로 코드를 짜면 시간 복잡도가 O(N)이다. 메모이제이션을 안하면 O(2**N)이다.