[프로그래머스_Python] 완전탐색 - 소수 찾기 [Lv. 2]

황준성·2024년 11월 5일

프로그래머스

목록 보기

9/14

문제

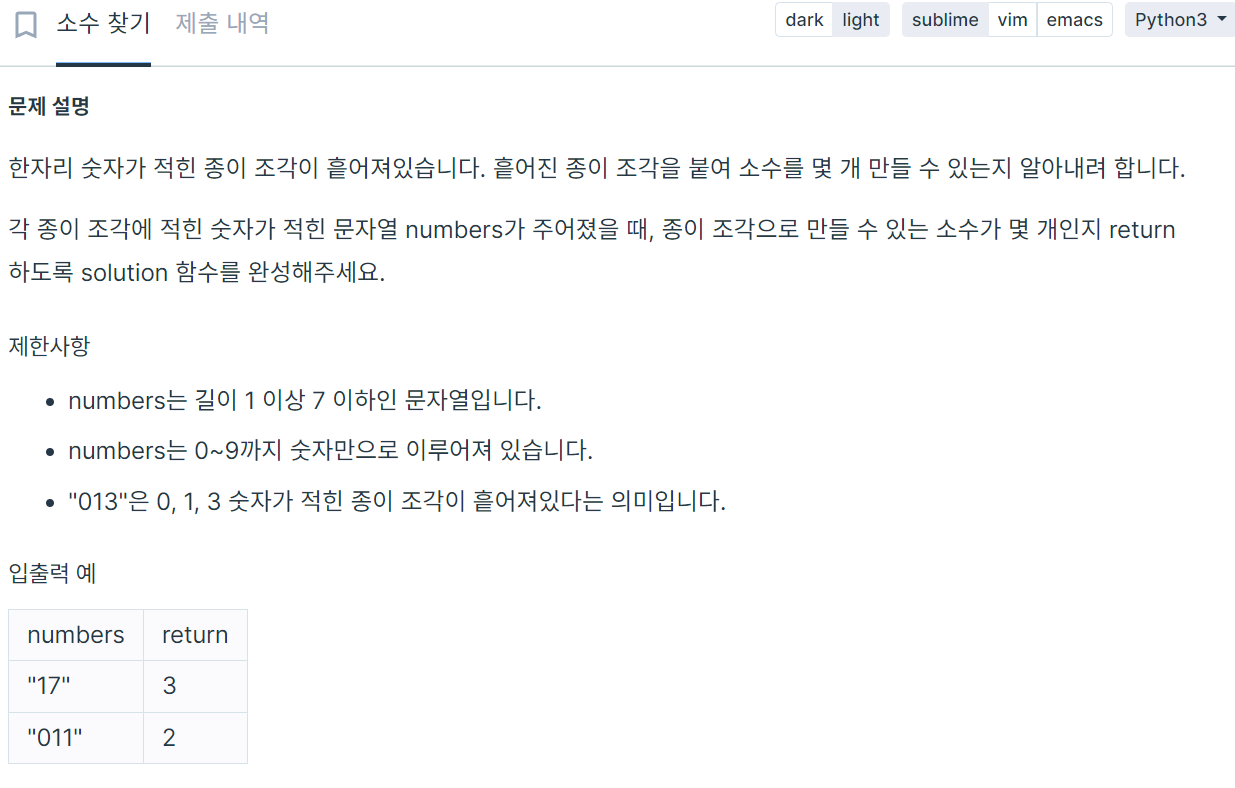
문제 이해

하.. 이 문제 애좀 먹었다. 수학 놓고 군대를 다녀와서 그런지 순열 조합 개념이 날아갔다. 뭐 어떻게 푸나 싶었는데 순열을 이용하는 문제였다. 그리고 파이썬을 사용하고 순열을 이용하는 것도 처음이라서 모듈이나 그런 것도 찾아보고 익혀야 했다. 사실 모듈을 사용한 적이 이번 말고 한 번 정도 밖에 없었다. 파이썬은 왠만하면 다 기본내장함수로 포함되어서 그런지 모듈을 이용할 일이 적다. 그래서 더 편하기 한 것 같다.

아무튼 이 문제를 풀려면 두 가지 지식이 필요하다.

에라토스테네스의 체 (소수 구하는 효율적인 방법)

순열 (permutations) 모듈 사용법

에라토스테네스의 체

아래의 설명은 밑의 링크에서 가져왔다.
https://daebaq27.tistory.com/106

사실 이건 학부생 1학년때 접했던 기억이 있다. 그런데 군대 다녀오고 문제를 안풀다보니 머릿속에서 잊혀진 것 같다. 그리고 학부생 1학년 때는 잘 몰라서 머릿속에 각인이 되지 않은 이유도 있을 거다.

일반적으로 소수를 구하는 방법

def is_prime_number(n):
    for i in range(2,n): # 2부터 n-1까지
        if n % i == 0: # 하나라도 나누어 떨어지는 수가 있다면
            return False # 소수가 아니다.
	
    return True

위의 방법은 직관적이지만 비효율적이라는 단점이 있다. 2부터 n-1까지 반복해야 하기에 O(n)의 시간 복잡도를 갖는다.

약수를 판단하는 데에는 기본적으로 2부터 n-1까지 모두 반복할 필요가 없다. 각 수가 갖는 약수는 해당 수의 제곱근을 기준으로 대칭을 이루기 때문이다. 16의 경우 1,2,4,8,16의 약수를 갖고 16의 양의 제곱근인 4를 기준으로 대칭을 이룬다. 즉, 16이 2로 나누어 떨어짐을 알게 된다면 8로 나누어 떨어지는 건 자동적으로 참이다. 16을 2로 나눈 몫이 8이기 때문이다.

즉, 제곱근 까지만 반복문으로 돌리면서 2이상으로 나누어 떨어지면 소수가 아닌 것이다. 반복문의 반복 횟수를 루트만큼 줄여주는 방식이다. 그래서 이 이론을 사용하면 시간 복잡도가 O(√n)이 된다.

에라토스테네스의 체를 이용한 방법

def is_prime_number(n):
    end = int(n**(1/2))
    for i in range(2, end+1):
        if n % i == 0:
            return False
    
    return True

순열 모듈

아래의 두 링크를 활용했다.
https://seu11ee.tistory.com/5

https://velog.io/@yeseolee/python%EC%9C%BC%EB%A1%9C-%EC%88%9C%EC%97%B4%EA%B3%BC-%EC%A1%B0%ED%95%A9-%EC%A7%81%EC%A0%91-%EA%B5%AC%ED%98%84%ED%95%98%EA%B8%B0

틀린 코드

# 프로그래머스_완전탐색_소수찾기
# 순열 모듈 import
from itertools import permutations

def isPrime(n):
    n = int(n)
    if n < 2:
        return False
    
    # 에라토스테네스의 체를 이용
    for i in range(2, int(n**(1/2))+1):
        if n % i == 0:
            return False
                   
    return True

def solution(numbers):
    # 소수 카운트
    cnt = 0
    # 순열 리스트
    permutation_list = []
                   
    for i in range(len(numbers)):
        permutation_list += list(map("".join, permutations(numbers, i+1)))
    
    # set()으로 중복을 없앤다
    permutation_list = set(permutation_list)
    permutation_list = [int(value) for value in permutation_list]
    
    for value in permutation_list:
        if isPrime(int(value)):
            cnt += 1
        
                   
    return cnt

틀린 이유
"011"이라는 값을 넣었을 때, permutation_list안에는 "011", "11"은 다른 것이기때문에 set()을 써도 중복처리가 되지 않는다. 하지만 먼저 int로 형변환을 하고 set()을 이용하면 둘다 "11"이 되기 때문에 중복처리로 걸러진다.
오답 풀이

# set()으로 중복을 없앤다
    permutation_list = set(permutation_list)
    permutation_list = [int(value) for value in permutation_list]

정답 풀이

# set()으로 중복을 없앤다
    permutation_list = [int(value) for value in permutation_list]
    permutation_list = set(permutation_list)

정답 코드

# 프로그래머스_완전탐색_소수찾기
# 순열 모듈 import
from itertools import permutations

# 에라토스테네스 체 이론 (소수 구하기)
def isPrime(n):
    n = int(n)
    if n < 2:
        return False
    
    # 에라토스테네스의 체를 이용
    for i in range(2, int(n**(1/2))+1):
        if n % i == 0:
            return False
                   
    return True

def solution(numbers):
    # 소수 카운트
    cnt = 0
    # 순열 리스트
    permutation_list = []
                   
    for i in range(len(numbers)):
        # "".join을 해서 permutations가 순열을 각각 괄호로 묶어주는 걸 붙여줌.
        permutation_list += list(map("".join, permutations(numbers, i+1)))
    
    # set()으로 중복을 없앤다
    permutation_list = [int(value) for value in permutation_list]
    permutation_list = set(permutation_list)

    # 소수인지 판별
    for value in permutation_list:
        if isPrime(int(value)):
            cnt += 1
        
                   
    return cnt

필요 스킬셋

set()

set함수는 값을 중복없는 조합으로 만들어준다.

"".join(list)

리스트의 값을 ""안에 해당하는 값으로 구분하여 붙여준다.

list = ['A', 'B', 'C']
print("".join(list))

# 출력: ABC

황준성

Make progress

이전 포스트

[프로그래머스_Python] 완전탐색 - 모의고사 [Lv. 1]

다음 포스트

[프로그래머스_Python] 완전탐색 - 소수 찾기 [Lv. 2]