1. 문제 파악
‘Skeletons’ 문제 해결에 있어서 가장 중요한 부분은 문제 상황이 무엇인지 이해하는 과정이다. 영문으로 작성된 문제이고, 문제의 설명부에 미사여구가 많이 포함되어 있기 때문이다.
- 복수의 마을이 존재하고, 각 마을은 단-방향의 길로 연결될 수 있다. (유향그래프)
- 최초 시점에, 모든 마을에는 각각 하나의 스켈레톤 병정이 할당된다.
- 스켈레톤들은 멈추지 않고 매 초마다 무조건 움직인다(길을 건넌다).
- 각 스켈레톤에는 정해진 목적지가 있으며, 모든 마을은 각각 하나의 스켈레톤의 목적지 대상이 된다.
- 특정한 시간 t 초 후에 스켈레톤의 위치는 모두 각자에게 정해진 목적지와 일치해야 한다.
- 이러한 임의의 시간 t 초가 존재할 수 있는 마을 구성인지를 프로그래머가 판단한다.
- 셀프 사이클인 길을 가지는 마을이 있을 수 있다.
즉, 문제 조건을 통해 알 수 있는 사실은, 우리가 판단해야 하는 것은 t 초가 정확히 몇 초인지가 아니라, 충분히 많은 시간이 흐르더라도 결국 최종적으로 모든 스켈레톤들이 본인들에게 정해진 적절한 목적지로 이동해있는 순간이 주어진 그래프에서 존재할 수 있느냐를 판단하는 것이다. 즉, 유향 그래프의 구성 상태를 판단하는 문제이다.
2. 초반 설계
유향 그래프에서 각 위치에 할당된 스켈레톤들이 제자리를 찾아가기 위해선 어떠한 조건이 있을까. 잠깐의 고민 후에 떠오른 생각은 아래와 같다.
- 우선, 특정 마을에서 출발한 경우, 어떠한 경로를 거쳐서 다시 돌아올 수 있어야 한다. 1번 마을에 1번 병정이 있고, 2번 마을에 5번 병정이 있다고 해보자. 5번 병정은 5번 마을로 가야 하고, 어딘가에 있는 2번 병정도 2번으로 가야 한다. 이때, 병정들은 무조건 멈추지 않고 움직이므로, 1번 병정도 움직여야 하는데, 결국 제자리로 돌아와야 한다. 즉, 유향 그래프에 사이클이 있어야 하고, 쉽게 말해 유향 그래프가 강하게 연결된 하나의 요소여야 한다.
-
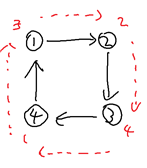
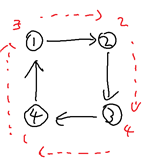
하나의 사이클로만 연결된 그래프는 옳지 않다. 만약, 우측 그림과 같이 단 하나의 사이클을 이루는 유향 그래프가 있다면, 최초에 배치된 병정들의 Circular 순서가 아무리 병정들이 사이클을 따라 움직인다고 해도 변하지 않기 때문이다.
-
사이클이 두 개 이상이면 병정들의 순서 시퀀스의 분배(분기? 가지치기?)가 가능해진다. 병정들은 멈추지 않고 움직이며, 시간 t 초에는 제한이 없으므로 사이클이 아래의 (a) 그림과 같이 두 개 이상 있으면 임의의 과정과 시간을 거친 후 결국 병정들이 제자리를 찾을 수 있게 될 것이다. 셀프 사이클도 가능하다고 했으므로 (b)와 같은 그래프도 가능하다.
그림(a) 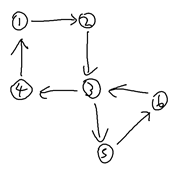 그림(b)
그림(b) 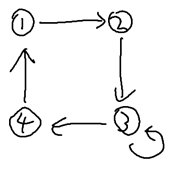
즉, 사이클 경로가 두 개 이상인 유향 그래프를 찾는 알고리즘을 설계해야 한다.
한편, 시간 t를 찾을 수 없는 그래프에는 어떤 모양들이 있을까. 본인이 찾은 몇 가지 상황은 다음과 같이 분류할 수 있다.
※ 시간 t초를 찾을 수 없는, 즉, 출력이 ‘N’인 상황
가장 간단하게 떠올려볼 수 있는 ‘N’ 상황은 아래와 같이 크게 세 가지 정도가 있을 수 있다.
(A) 병정이 이동하면 더이상 되돌아올 수 없는, 고립된 정점들이 존재하는 경우
(B) 애초에 사이클이 하나도 없는 경우
(C) 사이클이 하나만 있는 경우 – 앞 장의 예시처럼
조건(A) 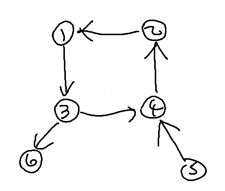
조건(B) 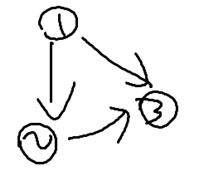
이를 위해선 그래프 및 사이클 탐색이 필요하고, 본인은 학교 알고리즘 수업에서 배운 ‘오일러 사이클 탐색 알고리즘’에서 아이디어를 따왔다. 물론 본 문제의 입력은 유향 그래프이지만, 스택을 활용한 변형된 형태의 DFS를 통해 그래프를 탐색하고, 지나온 경로를 기록해둘 수 있기 때문이다. 자세한 내용은 다음 항목에서 서술할 것이다.
한편, 위의 조건 (A)는 DFS 탐색과 별개로 입력 과정에서 간단한 반복문으로 판별할 수 있다. 입력받을 때 각 정점의 Incoming Edge 유무 여부와 Outgoing Edge 유무 여부를 bool 변수에 기록해두는 것이다. 그런 다음 입력 과정이 끝난 후에, 간단한 O(n) (n : 정점의 개수) 반복문을 통해 (A) 예시들을 걸러낼 수 있다.


이때, 두 번째 반복문은 혹시 있을 수 있는 ‘똑같은 방향 간선’ 입력을 무시하는 작업을 수행한다. 유향 그래프의 사이클을 DFS로 탐색할 때 동일한 간선을 굳이 여러 번 체크할 필요 없게 하기 위함이다. 이는 특히나 정점과 간선의 개수가 매우 많아질 때 유용히 사용될 수 있다. 물론, 이 과정 자체의 근본적인 복잡도는 ‘Quadratic Big-Oh’지만, 일반적인 그래프 입력은 적절히 분배된 형태이기 때문에 확률적으로 보았을 때 효율성을 더 높이는 효과가 더 클 것이다.
3. 중반 설계
본격적으로 유향 그래프의 사이클 개수를 판별하는 변형된 형태의 DFS를 설계하자. 우선 기본적인 원리는 DFS와 같다. 이때, 재귀적인 형태가 아닌 Iterative 방식으로 구현하였는데, 본 문제의 최대 정점과 간선 개수를 고려해 스택 오버플로우를 피하기 위함이다.
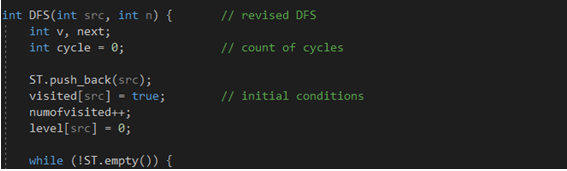
DFS 함수의 초반부이다. 간단한 초기화 과정을 수행하고 있다. cycle 변수는 사이클의 개수를 계수하고, ST는 STL 스택이다. visited 배열은 정점의 방문 여부를 기록하며, numofvisited와 level에 대한 설명은 하단에서 진행한다.
본 문제의 예시 입력을 시각적으로 그려 DFS를 디자인하자. 출력이 ‘Y’인 예시이다.
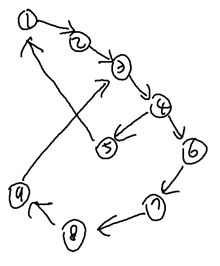

정점 1에서 탐색을 시작한다고 해보자. 미-방문 노드로 연결된 간선을 따라 2로 간다. 마찬가지 방식으로 4까지 간다. 스택에는 { 3 2 1 }이 들어 있다. 전형적인 DFS가 진행 중이다. 정점 4에서는 아무 간선을 택해 이동한다. 여기선 6을 택했다고 가정하자. 이어서 9까지 연달아 방문한다. 현재 스택에는 { 9 8 7 6 4 3 2 1 }이 들어 있다(참고로, 간선을 지나갈 때, 지나간 간선은 인접리스트에서 제거한다).
정점 9의 간선은 ‘9 -> 3’ 하나로 이를 확인하는데, 목적지 정점 3이 visited이다. 따라서 방문하지 않는다. 이때, 우리는 다음과 같은 포인트를 찾을 수 있다.
“DFS로 그래프를 탐색하다가 visited 정점을 맞닥뜨리면, 그 순간 사이클이 하나 형성된다.”
이어서, 남아 있는 간선이 없는 정점들이 스택에서 모두 빠져서 스택이 { 4 3 2 1 }인 상황으로 온다. 정점 4에는 아직 남아 있는 간선이 있고, 그 길을 따라 정점 5로 이동한다. 그리고 정점 5에서 간선을 따라 정점 1에 도달한다. 정점 1은 이미 방문한 노드이고, 따라서 사이클을 하나 더 발견했다. 나머지 스택의 원소들은 모두 Pop 되고, DFS는 종료되며, 발견한 사이클은 2개로 ‘Y’인 상황이다.
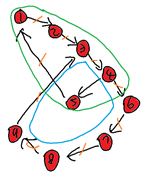
여기까지는 일반적인 과정의 DFS이다. 그런데, 다음의 예시를 통해 변형이 필요함을 확인할 수 있다.
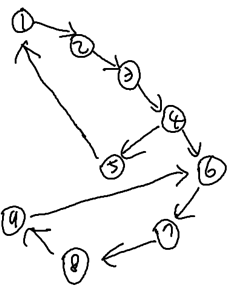
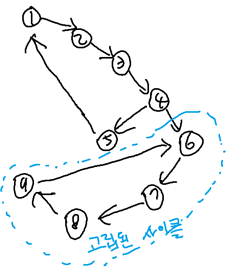
위와 같은 유향 그래프가 주어졌다고 해보자. 이는 출력이 ‘N’인 예시이다. 실제로 정점 4에서 정점 6으로 병정들이 이동하면 더 이상 해당 병정은 절대 { 1 2 3 4 5 1 } 사이클 부분으로 돌아갈 수 없다. 그런데, 만일 앞 장에서의 일반적인 DFS를 수행하면 단순히 사이클이 2개라고 감지하고 ‘Y’를 출력하게 된다.
이를 처리하기 위해서 다음을 추가한다.
“정점 v에서의 간선을 지나 visited 정점을 맞닥뜨리면, 거쳐온 경로를 추적해 해당 visited 정점과 정점 v 사이의 경로에서 또 다른 분기 가능 간선이 있는지를 확인한다.”
위의 예시를 통해 설명하자면, 정점 9에서 간선을 따라 visited 정점 6을 만나면, 정점 9에서 정점 6까지 역추적하는 과정에서 또 다른 분기 가능 정점이 있는지를 보는 것이다. 왜냐하면, 위의 예시 그림처럼 만일 그 경로에서 분기 가능 정점이 없다면, 해당 사이클은 고립된 사이클인 것이기 때문이다. 그리고 고립된 사이클이 있다면, 그 그래프는 곧 ‘N’인 그래프인 것이다(간선을 지나갈 때마다 간선을 인접리스트에서 지워버리기 때문에 이와 같은 추론은 합리적이다). 고립된 사이클의 경우 사이클 개수로 세지 않는다. 이러한 고립 사이클 존재 상황은 유향 그래프가 더 복잡하더라도, 이어지는 아래의 내용의 조건문에서 사용되는 numofvisited라는 변수에 의해 계속 카운트되지 않으며, 결국 ‘N’으로 판별된다.
그런데 ‘Y’인 상황을 가정했을 때는, 가장 마지막으로 검출되는 사이클의 경우 경로에서 더 이상 분기 가능한 정점이 없을 것이다(앞 장의 ‘Y’ 예시 시뮬레이션에서 { 1 2 3 4 5 1 } 사이클 탐색 상황이 바로 이 경우). 따라서 이를 위해 조건문이 필요할 것이다.
분기 가능 정점을 찾았든, 못 찾았든, 위의 과정이 마무리되면 맞닥뜨린 정점까지 스택을 Pop 한다. 만일 예시 그림에서 정점 9가 정점 6 말고 7이나 8과 연결되어도 마찬가지이다. 4와 연결되는 경우엔 ‘Y’인 상황임이 자명하며, 3, 2, 1과 5도 마찬가지로 ‘Y’인 상황이다.
지금까지 설명한 내용을 코드로 나타내면 아래와 같다. DFS 함수 내부이다.
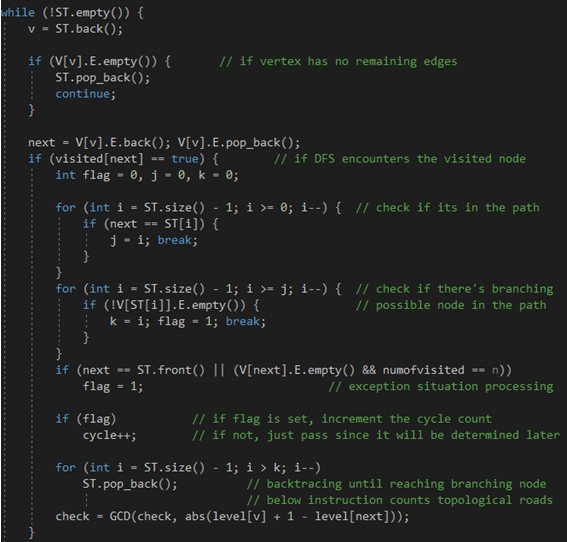
변수 flag는 정상적인 사이클을 찾았음을 의미한다. 하단의 check 변수와 GCD 유클리드 호제법에 대한 내용은 조금 뒤에 이어서 설명할 것이다.

위 코드는 미-방문 노드를 만났을 때의 DFS 동작을 수행한다. 전형적인 DFS 형태로 이뤄지며, 다만 앞서 설명한 마지막 사이클 감지 상황을 판단하기 위한 numofvisited 변수의 increment 과정이 있음에 유의하자. 방문할 정점의 간선 유무를 판단하는 조건문이 포함되어 있는데, 이는 설계 과정에서 작성했던 것으로, 사실 현시점에서는 필요 없는 동작이다. 고립 정점을 감지하기 위한 조건문인데, 어차피 메인에서 수행되는 ‘Incoming Edge와 Outgoing Edge’ 반복문에 의해 고립 정점은 필터링될 것이기 때문이다.
level과 check 변수가 없다고 가정하고, 위의 코드를 동작시키면 놀랍게도 대부분의 예시 유향 그래프들을 문제없이 통과한다. 아래와 같이 다양한 그래프들을 일일이 만들어 테스트해보았고, 모두 통과하였다.
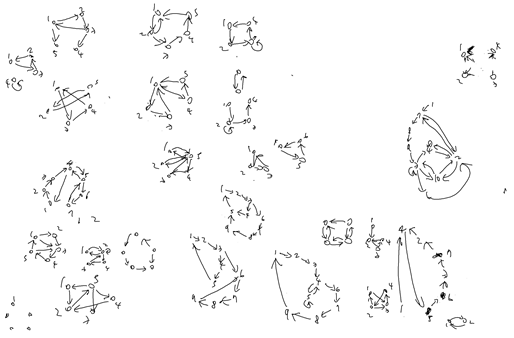
이 알고리즘에, 추가적으로 검산 목적으로 메인 함수에서 DFS 수행 이후의 visited 배열 상태를 확인해주면(모든 정점을 다 방문했는지. 물론 꼭 필요한 과정은 아님), 거의 대부분의 유향 그래프 입력을 처리할 수 있게 된다.
4. 후반 설계
하지만 앞선 단계까지의 DFS 알고리즘으로는 백준 온라인 저지를 통과하지 못한다. 상상할 수 있는 대부분의 유향 그래프에 대해서 잘 동작함을 확인했음에도 말이다. 사실, 4번 항목까지의 설계는 오랜 시간이 걸리지 않았었다. 곧 설명할 ‘마지막 반례’와 그 해결법을 찾기가 정말 오래 걸렸다.
아래의 그림을 확인해보자. 4번 항목까지의 알고리즘에서는 아래의 유향 그래프를 기본적으로는 ‘N’으로 판별하지만, 경우에 따라서는 ‘Y’로 판별할 수도 있다. 이 그래프는 고립된 사이클을 가지고 있다.

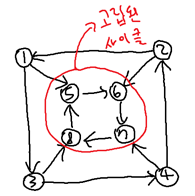
앞선 알고리즘으로 이 유향 그래프는 ‘N’ 판별이 충분히 가능하다. 예를 들어 정점 1에서 탐색을 시작하면, 바로 정점 5로 가거나, 혹은 정점 3을 거쳐서 8로 가거나 하면 고립 사이클을 발견해 ‘N’을 감지할 수 있다. 하지만, 만약 운이 없어서 DFS의 방문 순서가 ‘1 -> 3 -> 4 -> 2 -> 6 -> 7 -> 8 -> 5’가 되면 앞선 알고리즘은 이를 ‘Y’로 판별한다.
이 원인이 무엇일까. 그리고 이를 해결하기 위해선 기존의 알고리즘을 크게 헤치지 않는 선에서 어떻게 해야 할까? 이를 알아내기 위해 꽤나 오랜 시간 인터넷에서 유향 그래프와 위상 정렬 등의 개념을 계속 공부하고 고민해보았지만, 끝내 그럴듯한 이유를 찾아낼 수 없었다. 그러던 중 우연히 다음과 같은 생각이 들게 되었다.
“사이클이 단순히 2개 이상이라고 해서 무조건 모든 병정들이 모든 마을로 각각 분배될 수 있다고 단정할 수 있는가?”
예를 들어 보자. 앞서 보았던 표준 예시와, 그 예시를 조금 변형한 예시이다.

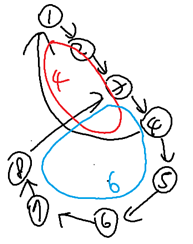
좌측 그림부터 보자. 앞서 보았던 표준 예시와 같고, ‘Y’인 상황이다. 바로 이어서 우측 그림도 보자. 좌측 그림의 그래프와 유사한 꼴을 가지고 있다. 지금까지의 설명만을 토대로 우측 그림을 보면, 언뜻 보았을 때 사이클도 2개이고, 고립된 부분도 없고 의심의 여지 없이 ‘Y’ 출력 상황처럼 느껴진다.
하지만, 이 우측의 그래프는 임의의 위치에 배치된 병정들을 모두 제자리로 옮겨줄 수 있는 그래프가 아니다. 즉, ‘N’이다. 그 이유는 바로 이러하다.
예를 들어 1번 마을(정점)에 정점 5를 타겟으로 하는 스켈레톤 병정이 있다고 해보자. 가시성을 높이고자 이 위치를 A라고 두자. 두 사이클의 길이가 각각 4와 6이다. 이제 해당 병정이 움직인다고 해보자. 아래의 표는 병정이 이동할 수 있는 위치를 선형적으로 간단하게 나타낸 표이다. 두 번째 행은 위치 A에 더한 정수값을 정점의 개수 8로 나눈 나머지이다.

위의 표를 보면 알 수 있듯이, 위치 A에 있는 정점이 도달할 수 있는 위치는 위와 같이 한정적이다. 한편, 좌측의 표준 예시 그림도 위와 같은 논리로 표를 구성해보자. 좌측 그래프는 길이가 5, 6인 사이클 두 개를 가지고 있다. 정점은 9개이다.

좌측 그래프는 우측 그래프와 다르게 위치 A에서 출발해도 모든 정점에 도달할 수 있다는 것을 표를 통해 알 수 있다. 어떤 차이일까? 그것은 바로 두 사이클의 길이의 최대공약수에 있다. 만약, 2개 이상의 사이클을 가지는 특정한 유향 그래프의 복수의 사이클 길이들의 최대공약수가 1이 아닌 2나 3과 같은 수이면, 위의 우측 그래프와 같은 상황이 벌어지는 것이다.
이를 구현하기 위해 코드상에서, 매 사이클을 찾을 때마다 사이클의 크기를 기록해두어야 한다. 바로 이 기능이 상기한 level 배열을 통해 수행할 수 있다. DFS에서 소스 정점을 루트로 하는 신장 트리의 레벨을 기록하는 것으로, 일반적으로 간단한 그래프 관련 PS 문제를 해결할 때 누적 cost 계산을 하는 방식이다.
그리고 이렇게 찾은 사이클들의 크기가 위의 예시에서 5와 6의 관계처럼, 최대공약수가 1, 즉, 서로소인 관계가 만들어진다면 모든 병정이 유향 그래프를 임의의 시간 t초 만큼 돌아다닌 후 제자리를 찾을 수 있는 것이다. 자세한 코드는 앞에서 첨부한 코드에 이미 포함되어 있다. check 전역 변수를 이용하며, 이를 메인에서 이용한다.
이러한 흐름을 통해 ‘Skeletons’ 문제 해결 알고리즘이 완성되었다. 메인 함수에서 본 알고리즘이 처리하지 못하는 소수의 초기 조건들(예를 들어 정점과 간선이 1개인 경우, 또는 정점 2개로만 이루어진 단일 사이클들)에 대해서만 예외 처리를 해주면 모든 작업이 완성된다. 실제로 이 코드로 채점을 돌리면 아래와 같이 ‘맞았습니다.’가 뜨는 것을 확인할 수 있다. 공간 복잡도와 시간 복잡도는 본인을 제외한 다른 유저들의 답안과 비교했을 때 평균적인 수준을 보이고 있다.

전체 코드는 아래와 같다.
#include <iostream>
#include <vector>
// BOJ - 14193 Skeletons
using namespace std;
typedef struct {
bool in_edge = false; // if vertex has incoming edge
bool out_edge = false; // if vertex has outgoing edge
vector<int> E; // adjacent list structure
}Vertex;
Vertex *V;
bool *visited;
vector<int> ST; // stack used in DFS
int numofvisited; // number of visited vertices
int *level; // for topological direction checking
int check; // for topological direction checking
int GCD(int a, int b) { // euclidean algorithm for topological checking
if (b == 0) return a;
return GCD(b, a % b);
}
int DFS(int src, int n) { // revised DFS
int v, next;
int cycle = 0; // count of cycles
ST.push_back(src);
visited[src] = true; // initial conditions
numofvisited++;
level[src] = 0;
while (!ST.empty()) {
v = ST.back();
if (V[v].E.empty()) { // if vertex has no remaining edges
ST.pop_back();
continue;
}
next = V[v].E.back(); V[v].E.pop_back();
if (visited[next] == true) { // if DFS encounters the visited node
int flag = 0, j = 0, k = 0;
for (int i = ST.size() - 1; i >= 0; i--) { // check if its in the path
if (next == ST[i]) {
j = i; break;
}
}
for (int i = ST.size() - 1; i >= j; i--) { // check if there's branching
if (!V[ST[i]].E.empty()) { // possible node in the path
k = i; flag = 1; break;
}
}
if (next == ST.front() || (V[next].E.empty() && numofvisited == n))
flag = 1; // exception situation processing
if (flag) // if flag is set, increment the cycle count
cycle++; // if not, just pass since it will be determined later
for (int i = ST.size() - 1; i > k; i--)
ST.pop_back(); // backtracing until reaching branching node
// below instruction counts topological roads
check = GCD(check, abs(level[v] + 1 - level[next]));
}
else { // if encountered node is un-visited,
if (!V[next].E.empty()) { // just go to that vertex
visited[next] = true;
numofvisited++;
ST.push_back(next);
level[next] = level[v] + 1;
}
}
}
return cycle; // total nums of cycles if the graph satisfies conditions
}
int main(void) {
int n, m, f, r, res, no_flag;
while (1) {
no_flag = 0; check = 0; numofvisited = 0;
cin >> n >> m;
if (n == 0 && m == 0) break;
V = new Vertex[n + 1];
visited = new bool[n + 1]; // initialization
for (int i = 1; i <= n; i++) visited[i] = false;
level = new int[n + 1];
for (int i = 0; i < m; i++) {
int already = 0;
cin >> f >> r;
for (int j = 0; j < V[f].E.size(); j++) // ignore already inserted edges
if (V[f].E[j] == r) { already = 1; break; } // for efficiency
if (already == 0) {
V[f].E.push_back(r); // graph construction
if (f != r) {
V[f].out_edge = true; // for making such conditions
V[r].in_edge = true;
}
}
}
for (int i = 1; i <= n; i++) { // check if there's isolated single vertex
if (n == 1) break; // only except for when n is 1
if (V[i].in_edge == false || V[i].out_edge == false) {
no_flag = 1;
break;
}
}
if (n >= m && n != 1 && n != 2) no_flag = 1; // censor some 'do not need to check'
if (no_flag) cout << "N\n";
else {
if (n == 1 && V[1].E.back() == 1) cout << "Y\n"; // process for some execeptional
else if (n == 2 && V[1].in_edge && V[2].in_edge // input situations that this
&& V[1].out_edge && V[2].out_edge) cout << "Y\n"; // algorithm cannot handle
else {
res = DFS(1, n);
cout << check;
if (res >= 2 && check == 1) // if graph has more than two cycles, and only one
cout << "Y\n"; // directional topological route, then it's okay!!
else cout << "N\n"; // if not, it's NO!!
}
}
delete[] V; delete[] visited; delete[] level;
}
return 0;
}