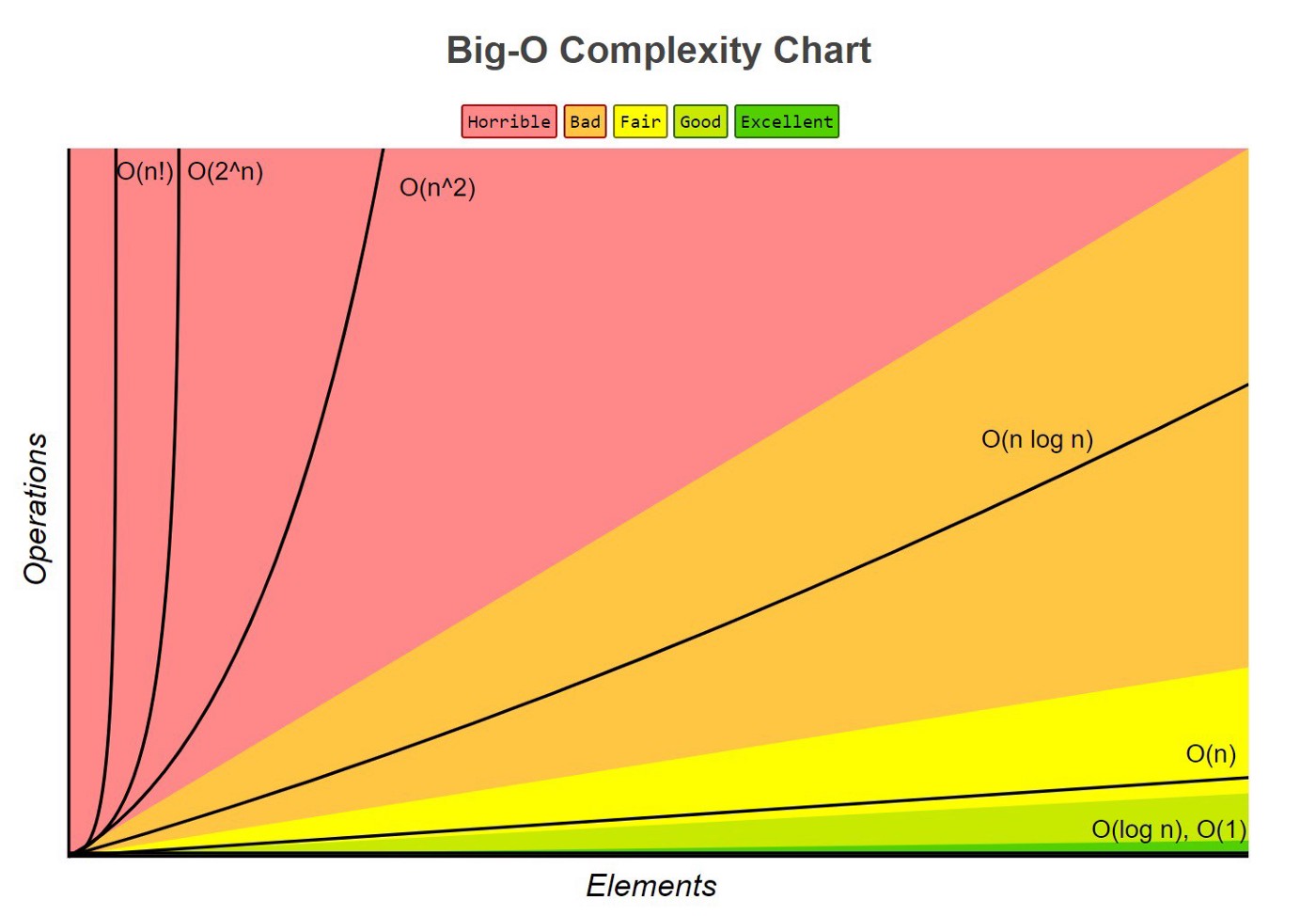
PS나 현업에서 특정한 문제를 해결할 때, 주어진 시간 제한을 엄격히 지키는 것이 중요하다. 학부 알고리즘 수업에서 다양한 시간 복잡도 관련 이론과 분석 방법에 대해 배웠지만, 사실 이를 실제 문제에 정확하게 적용하기란 쉽지 않다. 이때, (특히나 PS 문제 해결에서) 결코 정확하지는 않지만, 어느 정도 대략적인 기준점을 제시할 수 있는 매커니즘이 '알고리즘 문제 해결 전략 세트'에서 소개되고 있다. 그 내용은 다음과 같다.
(이 방식은 말 그대로 대략적인, '사상누각'에 불과한, 흔히 말하는 '야매(?)'이므로 결코 맹신해서는 안된다고 글쓴이 구종만씨는 강조한다. 하지만, 대부분의 경우 잘 맞아떨어진다고 한다.)
입력의 크기 N을 알고리즘의 시간 복잡도(빅오)에 대입해서 얻은 값(반복문의 수행 횟수)이 1억(10^8), 즉, 0이 8개가 넘어가면 1초라는 시간 제한을 초과할 가능성이 농후하다.
즉, 예를 들어 O(NlogN)인 알고리즘이 있고, 입력의 크기가 최대 10000, 시간제한이 1초라고 하면,
10000 x log_2(10000)은 명백히 1억보다는 (훨씬) 작은 값일 것이다. 이 경우엔 제한 시간을 초과하지 않을 것임을 확신하고 코딩을 시작하면 된다.
반대로, O(N^2)인 알고리즘을 같은 상황에 사용하는 경우 계산 값은 100,000,000로, 1억이다. 이 경우에는 '애매하다'라고 판단하면 된다. 만약, 사용한 알고리즘의 (가장 작은, 반복문에서 가장 최소에 해당하는) 내부 코드 블록이 복잡한 명령어나 과정을 거친다면 초과할 가능성이 높고, 간단하게 구성되어 있는 경우엔 시간 제한 내에 해결할 수 있을 가능성이 높다고 보면 편하다.
한편, O(N^3)인 알고리즘을 적용하면, 계산할 필요도 없이 초과할 것임을 알 수 있다. 즉, 이 경우엔 이 알고리즘을 적용하면 안되는 것이다.
여담) 재귀 호출이 사용되는 알고리즘의 경우, 또는, 관계식(점화식)으로서 알고리즘을 표현할 수 있는 경우엔 학부 알고리즘 수업에서 배웠던 Master Theorem을 이용해 복잡도를 추정해낼 수 있다. 아래와 같이 말이다.
※ Master Theorem
T(n) = aT(n/b) + p(n), p(n)이 Polynomial Function이고, 그 degree를 d라고 하자.
T(n) =
1) theta(n^d) if a < b^d
2) theta(n^d * logn) if a = b^d
3) theta(n^(log_b(a)) if a > b^d
이러한 Skill은 사용하는 언어와 그 언어의 옵션 설정 상태, 컴파일러의 성능, CPU의 성능, 클록의 주파수, 메모리 접근 방식, PC의 하드웨어 성능 등에 따라 언제든지 깨질 수 있는 법칙이다. 다만, 현 시점에서 최근의 PC 성능과 C++ 언어의 특성 등을 고려했을 때 PS 상황에서 가장 합리적으로 채택할 수 있는 '간단 분석법'이므로 그 유용성은 꽤나 있다고 볼 수 있다.
'알고리즘 문제 해결 전략 세트' 교재에 보다 더 자세한 설명이 있으니 관심있는 사람은 책을 구매해 학습을 진행하면 되겠다.
