
베르트랑 공준
문제
베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다.
이 명제는 조제프 베르트랑이 1845년에 추측했고, 파프누티 체비쇼프가 1850년에 증명했다.
예를 들어, 10보다 크고, 20보다 작거나 같은 소수는 4개가 있다. (11, 13, 17, 19) 또, 14보다 크고, 28보다 작거나 같은 소수는 3개가 있다. (17,19, 23)
자연수 n이 주어졌을 때, n보다 크고, 2n보다 작거나 같은 소수의 개수를 구하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 케이스는 n을 포함하는 한 줄로 이루어져 있다.
입력의 마지막에는 0이 주어진다.
출력
각 테스트 케이스에 대해서, n보다 크고, 2n보다 작거나 같은 소수의 개수를 출력한다.
제한
1 ≤ n ≤ 123,456
에라토스테네스의 체
베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다.
일정 범위 내의 소수를 구할 수 있는 에라토스테네스의 체 알고리즘을 이용하여 문제를 풀이한다.
알고리즘
1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다.
2. 2부터 시작해서 나열된 수에서 지워지지 않은 수 중 가장 작은 2를 소수로 선택하고 2의 배수를 지운다.
3. 3도 지워지지 않았기 때문에 소수로 선택하고 3의 배수를 지운다.
4. 4는 지워졌기 때문에 넘어가고 5를 소수로 선택하고 5의 배수를 지운다.
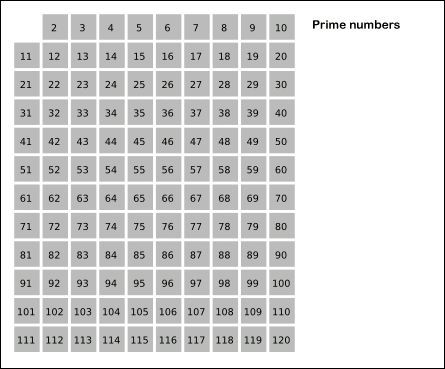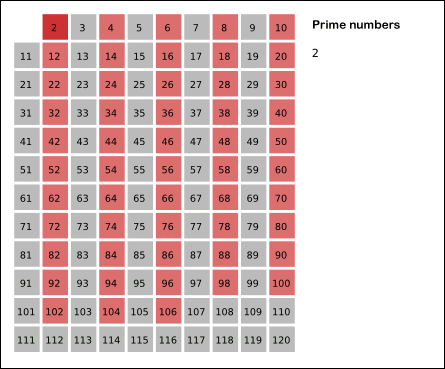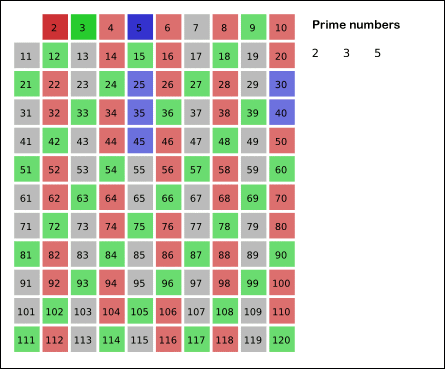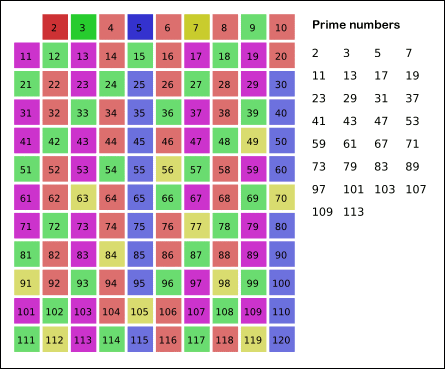
5. 2,3,4와 같은 과정을 반복한다.
6. 반복이 끝나면 지워지지 않은 수들을 소수로 출력한다.
코드
# 어떤 값이 들어오던지간에 최대 n은 123456이 되므로
# 2n인 246912까지의 소수를 미리 구해놓아 시간을 단축시킬 수 있다.
N = 123456 * 2 + 1
# 에라토스테네스의 체 파이썬 구현
sieve = [True] * N # N개 만큼의 True 배열을 만들어 놓는다.
for i in range(2, int(N**0.5)+1):
if sieve[i]:
for j in range(2*i, N, i):
sieve[j] = False
# for문을 돌면서 해당 숫자가 소수이면 소수의 배수들은 모두 False처리 한다.
# N**0.5는 N에 루트를 씌워준다는 의미
# 주어진 범위 내에 남아있는 True값(소수)의 수를 카운팅하는 함수
def prime_cnt(val):
cnt = 0
for i in range(val + 1, val * 2 + 1):
if sieve[i]:
cnt += 1
print(cnt)
while True:
val = int(input())
if val == 0:
break
prime_cnt(val)
# 인풋값 n(val)을 소수 카운팅 함수에 넣으며 값을 출력하다
# 테스트 케이스를 종료하는 입력값인 0을 입력받으면 break로 while문을 빠져나온다.