[이코테] 이진탐색 & DP

Nam_JU·2023년 9월 1일

16-1. 금광

금광의 모든 위치에 대하여, 3가지 경우(왼쪽 위에서 오는 경우, 왼쪽 아래에서 오는 경우, 왼쪽에서 오는 경우)를 비교하고,왼쪽에서의 가장 많은 금을, 현재 위치의 금에 더해줌으로써 문제를 해결해야함.

점화식

dp[i][j] += max(dp[i-1][j-1], dp[i][j-1], dp[i+1][j-1])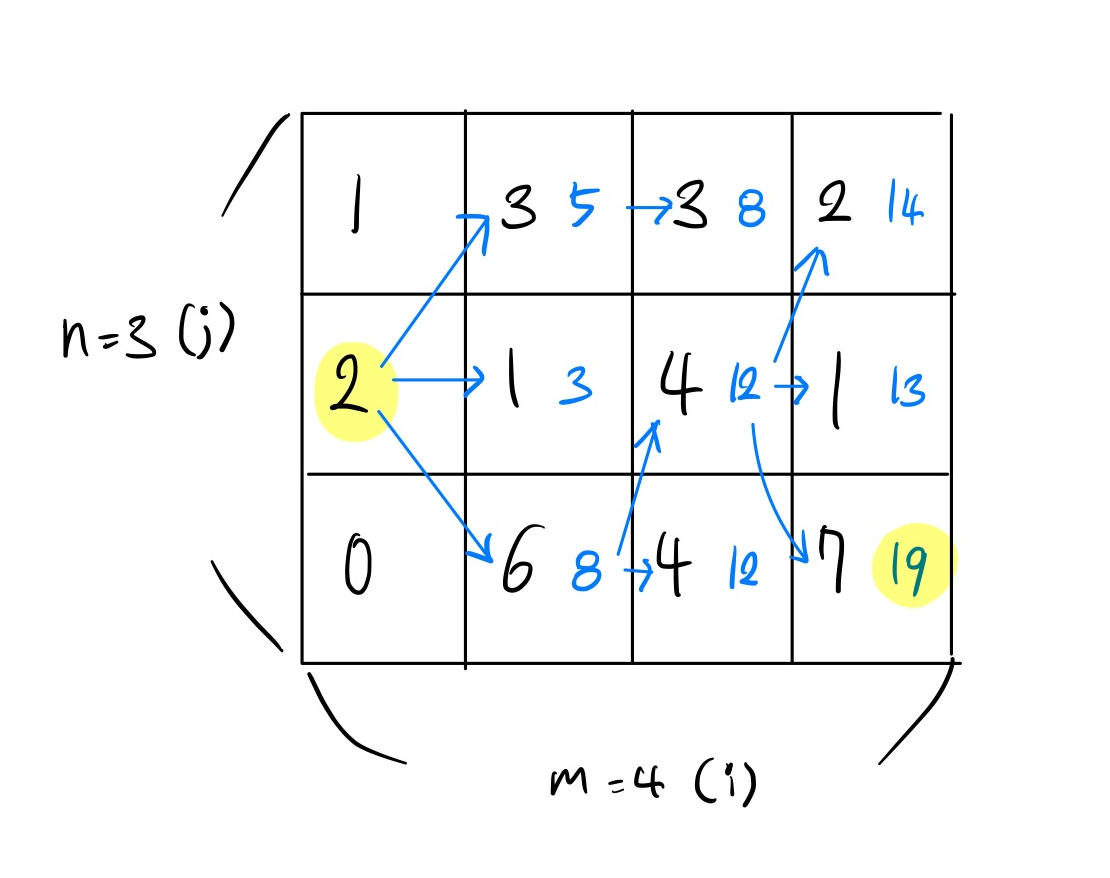

정답

"""
2
3 4
1 3 3 2 2 1 4 1 0 6 4 7
4 4
1 3 1 5 2 2 4 1 5 0 2 3 0 6 1 2
"""
import sys

# 테스트 케이스 입력
t = int(sys.stdin.readline())

for _ in range(t):
    # 금광 정보 입력
    n, m = map(int, sys.stdin.readline().split())
    gold_input = list(map(int, sys.stdin.readline().split()))

    # 다이나믹 프로그래밍을 위한 2차원 DP 테이블 초기화
    gold = []
    for i in range(n):
        gold.append(gold_input[i*m:i*m+m])

    # 다이나믹 프로그래밍 진행
    for j in range(1, m):
        for i in range(n):
            # 왼쪽 위가 없다면
            if ( i == 0 ):
                gold[i][j] += max(gold[i][j-1], gold[i+1][j-1])
            # 왼쪽 아래가 없다면
            elif ( i == n - 1):
                gold[i][j] += max(gold[i-1][j-1], gold[i][j-1])
            # 왼쪽 위와 왼쪽 아래가 다 있다면
            else:
                gold[i][j] += max(gold[i-1][j-1], gold[i][j-1], gold[i+1][j-1])

    # 채굴자가 얻을 수 있는 금의 최대 크기 비교
    result = 0
    for i in range(n):
        result = max(result, gold[i][m - 1])

    print(result)

16-2. 정수삼각형

계속 누적합을 하게 되어서 삼각형 형태의 크기 비교가 안됨

def solution(triangle):
    answer = 0
    s = len(triangle)
    graph = [[0] * s for _ in range(s)]
    graph[0][0] = triangle[0][0]
    maxV = -1e9

    for i in range(s-1):
        for j in range(s):
            graph[i+1][j]=triangle[i+1][j]+graph[i][j]
            maxV=max(maxV, graph[i][j])
    return maxV

정답

def solution(triangle):
    # dp 테이블 초기화
    dp = [[0] * len(triangle) for _ in range(len(triangle))]
    dp[0][0] = triangle[0][0]
    # 거쳐간 숫자의 최댓값 구하기
    for i in range(len(triangle) - 1):
        for j in range(len(triangle[i])):
            dp[i + 1][j] = max(dp[i + 1][j], dp[i][j] + triangle[i + 1][j])
            dp[i + 1][j + 1] = max(dp[i + 1][j + 1], dp[i][j] + triangle[i + 1][j + 1])

    return max(dp[-1]) # dp 테이블의 마지막 원소들 중 최댓값 반환

print(solution([[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]]))

16-3. 퇴사

뒤쪽부터 매 상담에 대하여 현재 상담 일자의 이윤(p[i]) + 현재 상담을 마친 일자부터의 최대 이윤(dp[t[i] + i]])을 계산

  dp[i] = max(p[i] + dp[t[i] + i], max_value)

"""
       1일    2일    3일    4일    5일    6일    7일
  Ti     3     5     1     1     2     4      2
  Pi    10    20    10    20    15    40    200
  
  7
3 10
5 20
1 10
1 20
2 15
4 40
2 200

"""

import sys

# 전체 상담 개수
n = int(sys.stdin.readline())

t = [] # 각 상담을 완료하는데 걸리는 기간
p = [] # 각 상담을 완료했을 때 받을 수 있는 금액

dp = [0] * (n + 1) # i번째 날부터 마지막 날까지 낼 수 있는 최대 이익

max_value = 0

for _ in range(n):
    x, y = map(int, sys.stdin.readline().split())
    t.append(x)
    p.append(y)

# 리스트를 뒤에서부터 거꾸로 확인
for i in range(n-1, -1, -1):

    # i번째 날짜에 상담이 가능한 경우
    if (i + t[i] <= n):
        # (현재 상담 날짜의 금액 + 다음 상담 날짜의 누적 금액)과
        # 현재 상담 날짜부터 마지막 날까지 쌓을 수 있는 최대 누적 금액을 비교
        dp[i] = max(p[i] + dp[i+t[i]], max_value)
        max_value = dp[i]
    # i번째 날짜에 상담이 불가능한 경우
    else:
        dp[i] = max_value

print(max_value)

16-4. 병사배치

[알고리즘] 최장 증가 부분 수열(LIS) 알고리즘

📌 최장 증가 부분 수열(LIS, Longest Increasing Subsequence)란?
원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중, 각 원소가 이전 원소보다 크다는 조건을 만족하고, 그 길이가 최대인 부분 수열을 최장 증가 부분 수열이라고 한다.

예를 들어, { 6, 2, 5, 1, 7, 4, 8, 3} 이라는 배열이 있을 경우, LIS는 { 2, 5, 7, 8 }이다
{ 2, 5 }, { 2, 7 } 등 증가하는 부분 수열은 많지만 그 중에서 가장 긴 것이 { 2, 5, 7, 8 }이다

16-5. 못생긴 수

시도1
while문을 사용하려고 하다가 꼬였다

"""
ugly = [2,3,5]
[1,2,3,4,5,6,8,9,12,15]

"""

n=int(input())
ugly = [2,3,5]
answer = [1]
cnt=1

while True:
    i=2
    for x in ugly: # [2,3,5]
        if i % x in ugly:
            answer.append(i)
        i += 1
        cnt += 1
    if cnt==n:
        print(answer)
        break
print(answer[n-1])

내코드 :
요즘 코테공부하면서 본 F,T를 사용해보기로함

n = int(input())
ugly = [False]*1001
ugly[1] = True

for i in range(2, 1001):
    if i%2==0:
        ugly[i] = True
    elif i%3==0:
        ugly[i] = True
    elif i%5==0:
        ugly[i] = True

answer = []
for i in range(len(ugly)):
    if ugly[i] == True:
        answer.append(i)
print(answer[n-1])

16-6. 편집거리

에러1 이동의 경우 고려안함

"""
편집거리

삽입 : 문자 추가
삭제 : 문자 삭제
교체 : 문자를 교체
SUNDAY
SATURDAY

SUNDAY #UN
SATURDAY #ATUR
S[A삽입][N삭제][T추가]U[R추가]DAY

같은 문자열이 있는지 확인 + 같은 문자열 따로 save[]=저장 // s2에 맞춰 문자열 순서 고려해야함(이동때문에)
save에 S2와 같은문자가 있으면 그대로 answer[] append (위치가 다르면 이동이됨!)
save에 없으면
"""

s1 = input() #sunday
s2 = input() #saturday
save = [] # SAYDU
answer = []
for i in range(len(s2)):
    if s2[i] in s1:
        save.append(s2[i])
# save에 중복 문자 들어옴 // 테케에서 오류남
save = set(save)
save = list(save)
cnt=0
for c in s2:
    if c in save:
        answer.append(c)
    else:
        answer.append(c)
        cnt+=1
print(cnt)

편집거리 알고리즘

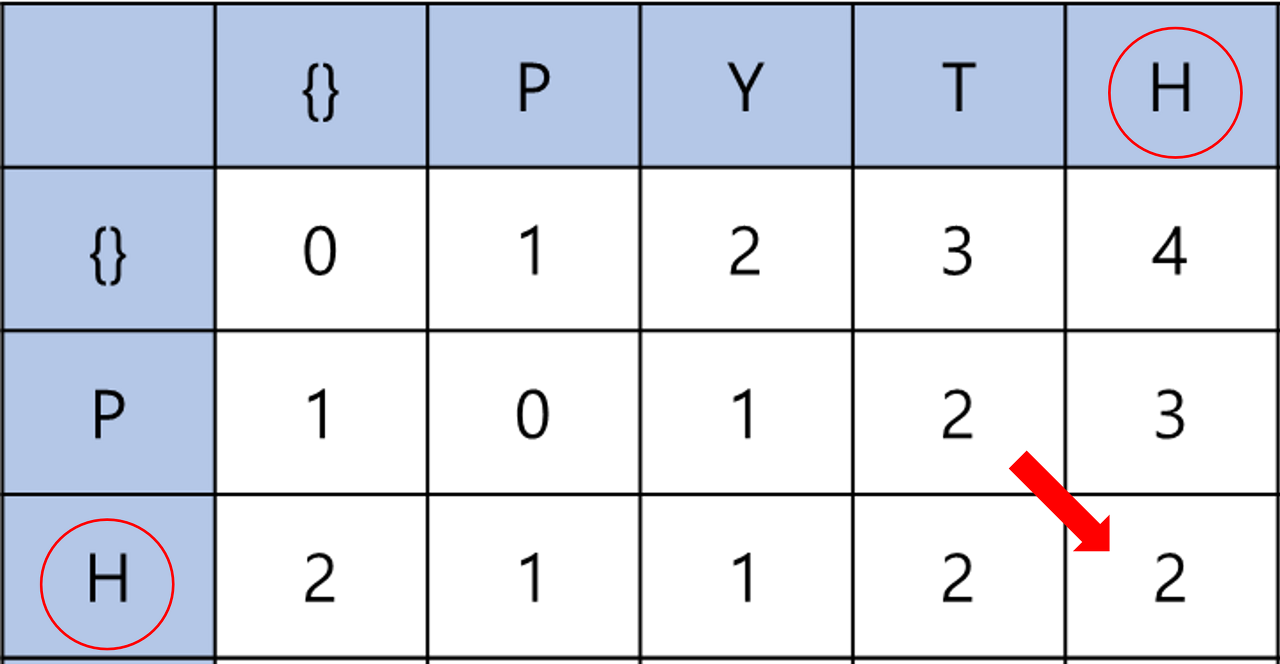
편집거리 알고리즘은 두 문자열의 유사도를 판단하는 알고리즘이다.

PYTHON, PHOTO
두값이 같으면 이전값을 그대로 가져오기
두값이 다르면 dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 중 최소값에 1을 더해서 dp[i][j]에 저장

비교

참고자료 : https://joyjangs.tistory.com/38

17 최단경로

17-1. 플로이드

INF = 1e9

# 도시(vertex), 버스(edge) 입력받기
N = int(input())
M = int(input())

# 플로이드-워셜은 2차원 배열이 필요하다.
graph = [[INF] * (N + 1) for _ in range(N + 1)]
for i in range(1, N + 1):
    graph[i][i] = 0

for _ in range(M):
    a, b, c = map(int, input().split())
    # 더 비용이 적다면 최신화
    graph[a][b] = min(graph[a][b], c)

for k in range(1, N + 1):
    for a in range(1, N + 1):
        for b in range(1, N + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

for x in range(1, N + 1):
    for y in range(1, N + 1):
        if graph[x][y] == INF:
            print(0, end=' ')
        else:
            print(graph[x][y], end=' ')
    print()