[이코테] 최단경로 알고리즘

• 문제사항
  • 한 지점에서 다른 한 지점까지 최단
  • 한 지점에서 다른 모든 지점까지 최단
  • 모든 지점에서 다른 모든 지점까지 최단

각 지점은 그래프에서 노드로 표현하고 지점 간 연결된 도로는 그래프에서 간선으로 표현

다익스트라 최단 경로 알고리즘

방법 1 : 간단한 다익스트라 최단 경로 알고리즘

• 한 지점에서 다른 모든 지점까지 최단, 음의 간선이 없을 때 정상적으로 동작한다.
• 이는 그리디 알고리즘으로 분류된다. 매 상황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복한다.
  
  

다익스트라 최단 경로 동작과정

1. 출발 노드 설정
2. 최단 거리 테이블 초기화 - 자기자신은 0
3. 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드 선택
4. 해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신합니다. (마지막 노드는 안해도 돼!) - 노드가 이미 처리된 적 있는 노드라면 무시
5. 위 과정 3,4 반복

이는 총 O(V)번에 걸쳐서 최단 거리가 가장 짧은 노드를 매번 선형 탐색해야 한다. 그리고 현재 노드와 연결된 노드를 매번 일일이 확인해야하기 때문에 전체 시간 복잡도는 O(V^2). 노드가 5000개 이하라면 가능하지만 10000개 넘어가면 비용이 높다. V : 노드의 개수

단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 매 단계마다 1차원 리스트의 모든 원소를 순차탐색 한다.

방법2 : 개선된 다익스트라 알고리즘 (힙 자료구조 사용)

스택 : 가장 나중에 삽입된 데이터 가장 먼저 추출(삭제)
큐 : 가장 먼저 삽입된 데이터 추출(삭제)
우선순위 큐 : 가장 우선순위가 높은 데이터 추출(삭제)

• 최소 힙 : 값이 낮은 것부터 순서대로
• 최대 힙 : 값이 높은 것부터 순서대로

우선순위 큐 구현 방식	삽입시간	삭제시간
리스트	O(1)	O(1)
힙	O(LogN)	O(LogN)

힙 라이브러리

• 우선순위 큐 구현하기 위해 사용하는 자료구조.
• 파이썬에서 힙 라이브러리는 최소 힙으로 되어있어서 힙을 삽입(heapq.heappush)하고 꺼내어 (heapq.heappop)담으면 오름차순으로 정렬된다.
• 최대힙을 사용하고 싶으면 부호를 반대로 삽입하고 부호를 반대로 꺼내어 담는다.
• 힙 자료구조 시간 복잡도 : O(ELogV)
• 노드를 하나씩 꺼내 검사하는 반복문은 노드의 개수 V이상의 횟수로는 처리되지 않는다.
  • 결과적으로 현재 우선순위 큐에서 꺼낸 노드와 연결된 다른 노드들을 확인하는 총횟수는 간선의 개수(E)만큼 연산이 수행될 수 있다.
• 직관적으로 전체과정은 E개의 원소를 우선순위 큐에 넣다가 모드 뺀 연산과 유사하다.

  데이터 수가 N개일 때, 힙 자료구조에서 데이터 모두 넣은 뒤 꺼낼 때 시간 복잡도는?
  - 삽입할 때 O(logN)의 연산을 N번 반복하므로 O(NlogN)이고 삭제할 때도 O(NlogN)이다. 따라서 전체 연산 횟수는 O(NlogN)임.

플로이드 워셜 알고리즘

• 모든 지점에서 다른 모든 지점까지 최단
• 거쳐 가는 노드를 기준으로 알고리즘을 수행한다. 하지만 매 단계마다 방문하지 않은 노드 중 최단거리를 갖는 노드를 찾는 과정이 필요하지 않다.
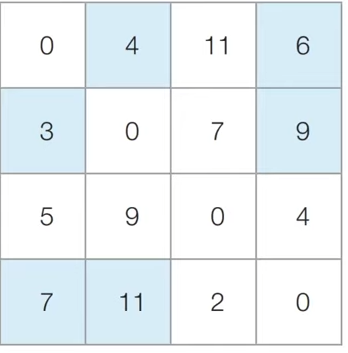
• 플로이드 워셜은 2차원 테이블에 최단 거리 정보를 저장한다.
• 다이나믹 프로그래밍 유형에 속한다.
• 각 단계마다 O(N^2)의 연산을 통해 현재 노드를 거쳐 가는 모든 경로를 고려한다. 따라서 총 시간 복잡도는 삼중 반복문을 사용하기에 O(N^3)이다. -보통 노드 500개 이하 때 사용

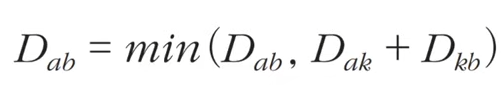
• a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사한다.

플로이드 워셜 알고리즘 동작과정
초기 상태 : 최단거리 테이블을 초기화한다. (거쳐가는거 고려x)

→

1번 노드를 거쳐 가는 경우를 고려해서 테이블을 갱신한다.
2,3,4번 노드도 마찬가지로 하나씩 확인해서 테이블 갱신한다.