[백준][1707번: 이분 그래프]

🎁문제

문제링크

그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.

그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.

🎁입력

입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.

🎁출력

K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.

🎁접근방법

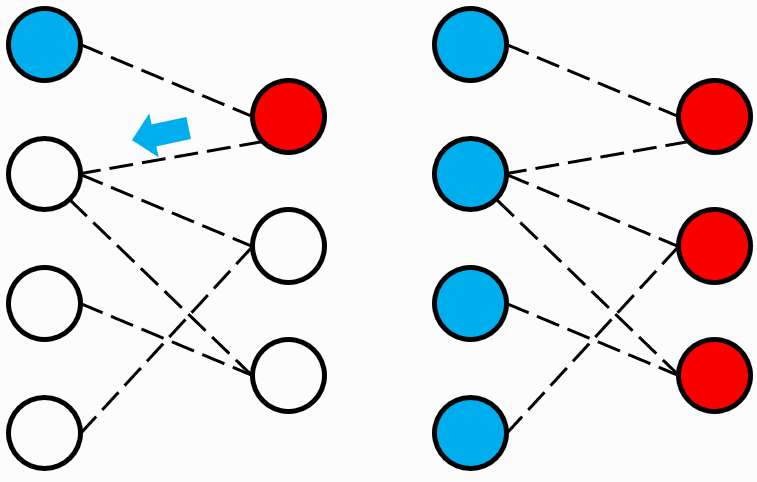
처음에는 문제 이해를 못해서 접근을 잘못했다. 처음에는 아래의 그림처럼 이해했다.
하지만 이분 그래프는 아래의 그림이다.

자기 자신이랑 연결된 부분들이 나와 다른 색깔(종류)여야하는 것이 이분그래프이다.
잘 알지 못하지만 이분 그래프 개념 (<---클릭해서 자세히 볼수 있다)

1. 저는 색깔로 구별했습니다.
2. bfs를 이용해서 풀었습니다.
   조건 1. 같은 색깔일 때, ans에 NO 저장 후 false 리턴
   조건 2. 아무 색깔이 없을 때, 현재 색깔이 RED면 visited에 BLUE로 처리 후 큐에 저장, 반대로 BLUE면 RED로 visited 방문처리 후 큐에 저장.
3. 모든 케이스가 끝나고 StringBuilder를 출력한다.

🎁코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {
    static int T;
    static int RED = 1;
    static int BLUE = -1;
    static String ans;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        T = Integer.parseInt(br.readLine());

        StringTokenizer st;
        for(int i=0; i<T; i++){
            st = new StringTokenizer(br.readLine());
            int V = Integer.parseInt(st.nextToken()); // 정점의 개수
            int E = Integer.parseInt(st.nextToken()); // 간선의 개수
            ArrayList<Integer>[] graph = new ArrayList[V+1];
            for(int j=1; j<=V; j++){
                graph[j] = new ArrayList<>();
            }
            for(int j=0; j<E; j++){
                st = new StringTokenizer(br.readLine());
                int u = Integer.parseInt(st.nextToken());
                int v = Integer.parseInt(st.nextToken());
                graph[u].add(v);
                graph[v].add(u);
            }
            int[] visited = new int[V+1];
            ans = "YES";
            for(int j=1; j<=V; j++) {
                if(visited[j]==0) {
                    if(!(check(j,graph, visited))) break;
                }
            }
            sb.append(ans).append('\n');
        }
        System.out.println(sb.toString());
    }
    static boolean check(int n, ArrayList<Integer>[] graph, int[] visited){
        Queue<Integer> queue = new LinkedList<>();
        queue.add(n);
        visited[n] = RED;

        while(!queue.isEmpty()){
            int now = queue.poll();
            for(Integer node : graph[now]){
                if(visited[node]==visited[now]){ // 자신과 같은 색깔일 때
                    ans = "NO";
                    return false;
                }
                if(visited[node]==0){
                    visited[node]=(visited[now]==RED)?BLUE:RED;
                    queue.add(node);
                }
            }
        }
        return true;
    }
}