[백준][1991번: 트리 순회]

🎈문제

문제링크

이진 트리를 입력받아 전위 순회(preorder traversal), 중위 순회(inorder traversal), 후위 순회(postorder traversal)한 결과를 출력하는 프로그램을 작성하시오.
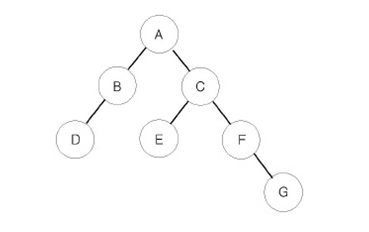
예를 들어 위와 같은 이진 트리가 입력되면,

• 전위 순회한 결과 : ABDCEFG // (루트) (왼쪽 자식) (오른쪽 자식)
• 중위 순회한 결과 : DBAECFG // (왼쪽 자식) (루트) (오른쪽 자식)
• 후위 순회한 결과 : DBEGFCA // (왼쪽 자식) (오른쪽 자식) (루트)
  가 된다.

🎈입력

첫째 줄에는 이진 트리의 노드의 개수 N(1 ≤ N ≤ 26)이 주어진다. 둘째 줄부터 N개의 줄에 걸쳐 각 노드와 그의 왼쪽 자식 노드, 오른쪽 자식 노드가 주어진다. 노드의 이름은 A부터 차례대로 알파벳 대문자로 매겨지며, 항상 A가 루트 노드가 된다. 자식 노드가 없는 경우에는 .으로 표현한다.

🎈출력

첫째 줄에 전위 순회, 둘째 줄에 중위 순회, 셋째 줄에 후위 순회한 결과를 출력한다. 각 줄에 N개의 알파벳을 공백 없이 출력하면 된다.

🎈접근방법

재귀를 통해서 전위,중위,후위 각각 해당하는 위치에서 StringBuilder에 값을 저장했다.

🎈코드

package BaekJoon.P1991;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;

/**
 * https://www.acmicpc.net/problem/1991
 * [1991번: 트리 순회]-Sliver1
 */

public class Main {
    static int N;
    static ArrayList<Node>[] tree;
    static StringBuilder sb = new StringBuilder();
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());

        tree = new ArrayList[N+1];
        for(int i=1; i<=N; i++){
            tree[i] = new ArrayList<>();
        }

        for(int i=0; i<N; i++){
            String[] ch = br.readLine().split(" ");
            int data = ch[0].charAt(0)-'A'+1;
            tree[data].add(new Node(ch[1].charAt(0), ch[2].charAt(0)));
        }
        preorder('A');
        sb.append('\n');
        inorder('A');
        sb.append('\n');
        postorder('A');
        System.out.println(sb.toString());
    }
    static void preorder(char node){
        if(node != '.') {
            sb.append(node);
            preorder(tree[node - 'A' + 1].get(0).left);
            preorder(tree[node - 'A' + 1].get(0).right);
        }
    }
    static void inorder(char node){
        if(node != '.') {
            inorder(tree[node - 'A' + 1].get(0).left);
            sb.append(node);
            inorder(tree[node - 'A' + 1].get(0).right);
        }
    }
    static void postorder(char node){
        if(node != '.') {
            postorder(tree[node - 'A' + 1].get(0).left);
            postorder(tree[node - 'A' + 1].get(0).right);
            sb.append(node);
        }
    }
    static class Node{
        char left;
        char right;

        public Node(char left, char right) {
            this.left = left;
            this.right = right;
        }
    }
}