그리디

이것이 취업을 위한 코딩 테스트다 with 파이썬 (나동빈 저) 의 책과 강의를 보고 정리한 글입니다.
강의 출처 : https://www.youtube.com/channel/UChflhu32f5EUHlY7_SetNWw

그리디 알고리즘

그리디 알고리즘은 지금 당장 좋은 것만 고르는 방법을 의미한다. 문제를 풀기 위한 최소한의 아이디어를 떠올릴 수 있는 능력을 요구한다.

그리디 해법은 그 정당성 분석이 중요한데 단순히 가장 좋아 보이는 것을 반복적으로 선택해도 최적의 해를 구할 수 있는지 검토한다

[문제 상황] 루트 노드부터 시작하여 거쳐 가는 노드 값의 합을 최대로 만들고 싶다. 최적의 해는?

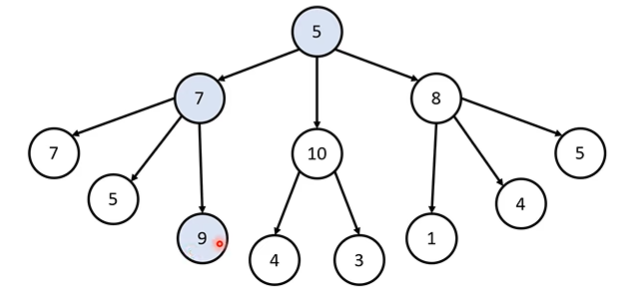
가장 높은 합을 만드는 최적의 해는 5 -> 7 -> 9이다.
가장 큰 값만 고른다면 5 -> 10 -> 4 총 19만큼 해가 나올 수 있다.

일반적인 상황에서 그리디 알고리즘은 최적의 해를 보장할 수 없을 때가 많다. 코딩 테스트에서 대부분 그리디 문제는 탐욕법으로 얻은 해가 최적의 해가 되는 상황에서 이를 추론할 수 있어야 풀리도록 출제된다.

<문제> 거스름 돈: 문제 설명

거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다고 가정할 때 손님에게 거슬러 주어야 할 돈이 N원일 때 거슬러 주어야 할 동전의 최소 개수를 구하시오. (N은 항상 10의 배수)

문제 해결 아이디어
최적의 해를 빠르게 구하기 위해서 가장 큰 화폐 단위부터 돈을 거슬러 준다.

# n = int(input("거스름 돈: "))
n = 1260
count = 0

# 큰 단위의 화폐부터 차례대로 확인하기
array = [500, 100, 50, 10]

for coin in array:
    count += n // coin  # 해당 화폐로 거슬러 줄 수 있는 동전의 개수 세기
    n %= coin

print(count)

가장 큰 화폐 단위부터 돈을 거슬러 주는 것이 최적의 해를 보장하는 이유는 동전 중에 큰 단위가 항상 작은 단위의 배수이므로 작은 단위의 동전들을 종합해 다른 해가 나올 수 없기 때문이다.

만약 800원을 거슬러 줘야 하는데 화폐 단위가 500원, 400원 100원 이라면?
위의 알고리즘을 사용하면 500원 1개 100원 3개 총 4개일 것이다.
하지만 최적의 해는 400원 2개로 총 2개이다.
위의 알고리즘으로 최적의 해를 보장할 수 없는 것이다. 500이 400의 배수가 아니기 때문에 문제가 발생하는 것이다.

이처럼 그리디는 최소한의 아이디어를 떠올리고 정당한지 검토해야 한다.

• 시간 복잡도 분석
  화폐의 종류의 개수가 K라면 시간 복잡도는 O(K)이다. K만큼 for문을 돌기 때문이다.

<문제> 1이 될 때까지: 문제 설명

어떠한 수 N이 1이 될 때까지 다음 두 과정 중 하나를 반복적으로 선택 수행.
단, 두번째 연산은 N이 K로 나누어 떨어질 때만 선택 가능

1. N -1
2. N / K

ex) N이 17 K가 4, 1번 과정 1번 후 2번 과정 2번 수행하면 N이 1이 된다.
결과적으로 전체 과정을 실행한 횟수는 3.

입력 조건 : 첫째 줄에 N(1~100,000)과 K(2~100,000)가 공백을 기준으로 하여 각각 자연수로 주어진다.
출력 조건 : 첫째 줄에 N이 1이 될 때까지 1번 혹은 2번의 과정을 수행해야 하는 횟수의 최솟값을 출력

# 내 풀이
# N, K = map(int, input("").split())

# if (N < 1 or N > 100000) or (K < 2 or K > 100000):
#     raise ValueError

# count = 0

# while(N > 1):
#     if N % K != 0:
#         N -= 1
#         count += 1
#     else:
#         N = N / K
#         count += 1

# print(count)

n, k = map(int, input().split())

result = 0

while True:
    # N이 K로 나누어 떨어지는 수가 될 때까지만 1씩 빼기
    target = (n // k) * k
    result += (n - target)
    n = target
    # N이 K보다 작을 때 (더 이상 나눌 수 없을 때) 반복문 탈출
    if n < k:
        break
    # K로 나누기
    result += 1
    n //= k

# 마지막으로 남은 수에 대하여 1씩 빼기
result += (n - 1)
print(result)

target = (n // l) * k
이 코드로 만약 n이 k로 나누어 떨어지지 않는다고 했을 때 가장 가까운 나누어 떨어지는 수를 구한다.
그리고 result += (n - target)으로 한번에 몇번 1을 빼야 하는지를 한줄로 해주는 것이다.
이렇게 작성하면 반복문 한번 돌 때 많은 일을 하기 때문에 반복 횟수에 따라 기하급수적으로 n이 빠르게 줄어든다. 즉 시간 복잡도가 O(log)가 되는 것이다. 이렇게 되면 n과 k가 매우 큰 수가 되더라도 빠르게 해결 가능하다.

<문제> 곱하기 혹은 더하기

<문제 설명>
각 자리가 숫자(0부터 9)로만 이루어진 문자열 S가 주어졌을 때, 왼쪽부터 오른쪽으로 하나씩 모든 숫자를 확인하며 숫자 사이에 'x' 혹은 '+' 연산자를 넣어 결과적으로 만들어질 수 있는 가장 큰 수를 구하는 프로그램을 작성하라. 단, 모든 연산은 왼쪽에서부터 순서대로 이루어진다고 가정

ex) 02984라는 문자열로 만들 수 있는 가장 큰 수는 ((((0+2)x9)x8)x4)=576이다.

입력 조건 : 첫째 줄에 여러 개의 숫자로 구성도니 하나의 문자열 S가 주어진다. (1 <= S의 길이 <= 20)
출력 조건 : 첫째 줄에 만들어질 수 있는 가장 큰 수를 출력한다.

# 내 풀이 
# a = list(input(""))
# if int(a[0]) == 0:
#     del a[0]

# result = int(a[0])

# for b in a[1:]:
#     if int(b) > 1:
#         result *= int(b)
#     else:
#         result += int(b)

# print(result)

data = input()

# 첫 번째 문자를 숫자로 변경하여 대입
result = int(data[0])

for i in range(1, len(data)):
    num = int(data[i])
    if num <= 1 or result <= 1:
        result += num
    else:
        result *= num

print(result)

<문제> 모험가 길드: 문제 설명

한 마을에 모험가 N명이 있다. 모험가 길드에서는 N명의 모험가를 대상으로 '공포도'를 측정했는데 길드장인 동빈씨는 공포도가 X인 모험가는 반드시 X명 이상으로 구성한 모험가 그룹에 참여해야 여행을 떠날 수 있도록 규정했다. 최대 몇 개의 모험가 그룹을 만들 수 있을까? N명의 모험가에 대한 정보가 주어졌을 때, 여행을 떠날 수 있는 그룹 수의 최댓값을 구하는 프로그램을 작성하시오.

ex) N = 5, 공포도 2 3 1 2 2
이 경우 그룹 1에 공포토가 1, 2, 3인 모험가를 한 명씩 넣고, 그룹 2에 공포도가 2인 남은 두명을 넣게 되면 총 2개의 그룹을 만들 수 있다.
또한 몇 명의 모험가는 마을에 그대로 남아 있어도 되기 때문에 모든 모험가를 그룹에 넣을 필요는 없다.

입력 조건 : 첫째 줄에 모험가 수 N(1 <= N <= 100,000 둘째 줄에 공백으로 구분된 공포도(N이하의 자연수)
출력 조건 : 여행을 떠날 수 있는 그룹 수의 최댓값을 출력한다.

# 내 풀이
# people = int(input(""))
# Fear = list(map(int, input("").split()))
# Fear.sort()

# result = 0
# group = []

# for a in Fear:
#     group.append(a)
#     if a <= len(group):
#         result += 1
#         print(group)
#         group = []

# print(result)

n = int(input())
data = list(map(int, input().split()))
data.sort()

result = 0 # 총 그룹의 수
count = 0 # 현재 그룹에 포함된 모험가의 수

for i in data: # 공포도를 낮은 것부터 하나씩 확인하며
    count += 1 #현재 그룹에 해당 모험가를 포함시키기
    if count >= i: # 현재 그룹에 포함된 모함가의 수가 현재의 공포도 이상이라면, 그룹 결성
        result += 1 # 총 그룹의 수 증가시키기
        count = 0 # 현재 그룹에 포함된 모함가의 수 초기화

print(result) # 총 그룹의 수 출력