이것이 취업을 위한 코딩 테스트다 with 파이썬 (나동빈 저) 의 책과 강의를 보고 정리한 글입니다.
강의 출처 : https://www.youtube.com/channel/UChflhu32f5EUHlY7_SetNWw
다이나믹 프로그래밍
메모리를 적절히 사용하여 수행 시간 효율성을 비약적으로 향상시키는 방법으로 이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 한다. 탑다운(하향식), 보텀업(상향식) 방식이 있다.
동적 계획법이라고도 부르는데 자료구조에서 동적 할당(Dynamic Allocation)은 프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법을 의미하지만 다이나믹 프로그래밍에서 다이나믹은 별다른 의미 없이 사용된다.
다이나믹 프로그래밍의 조건
- 최적 부분 구조 (Optimal Substructure) : 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
- 중복되는 부분 문제 (Overlapping Subproblem) : 동일한 작은 문제를 반복적으로 해결해야 한다.
피보나치 수열
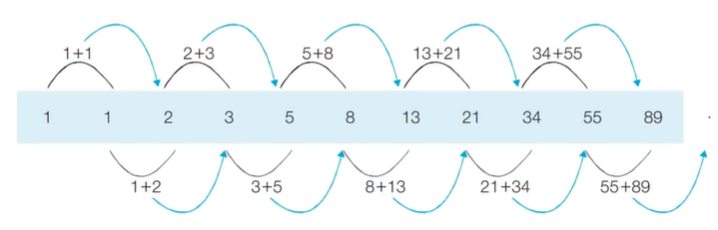
1,1,2,3,5,8,13,21,34,55,89,...
점화식이란 인접한 항들 사이의 관계식을 의미한다.
- 피보나치 수열의 점화식
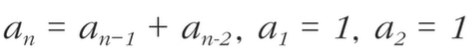
프로그래밍에선 수열을 배열이나 리스트를 이용해 표현한다.
# 피보나치 함수
def fibo(x):
if x == 1 or x == 2:
return 1
return fibo(x - 1) + fibo(x - 2)
print(fibo(4)) # 3
피보나치 수열의 시간 복잡도
단순 재귀 함수로 피보나치 수열을 해결하면 지수 시간 복잡도(O(2^N))이다. n이 커지게 되면 기하 급수적으로 시간 복잡도가 커질 것이다.
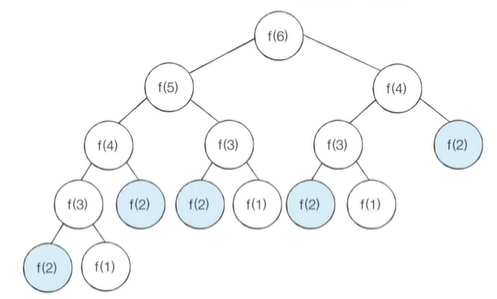
f(2)가 여러 번 호출되는 것을 확인할 수 있다. (중복되는 문제) f(2)는 이미 해결한 적이 있기 때문에 f(2)의 답을 별도의 메모리 공간에 기록해 놓아야 한다.
피보나치 수열의 해법 : 다이나믹 프로그래밍
다이나믹 프로그램 사용 조건 확인하기
1. 최적 부분 구조
2. 중복되는 부분 문제
피보나치 수열은 두 조건을 만족한다.
메모이제이션 (Memoization) - 탑다운(하향식)
다이나믹 프로그래밍을 구현하는 방법 중 하나로 한 번 계산한 결과를 메모리 공간에 메모하는 기법이다. 같은 문제를 호출하면 메모했던 결과를 그대로 가져온다. 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 한다.
탑다운 vs 보텀업
탑다운(메모이제이션) 방식은 하향식이며 보텀업은 상향식이다. 다이나믹 프로그래밍의 전형적인 형태는 보텀업 방식이다. 결과 저장용 리스트는 DP 테이블이라고 부른다.
메모제이션은 이전에 계산된 결과를 일시적으로 기록해 놓는 넓은 개념을 의미하기 때문에 다이나믹 프로그래밍에 국한된 개념은 아니다.
- 탑다운 방식
# 한 번 계산된 결과를 메모이제이션(Memoization)하기 위한 리스트 초기화
d = [0] * 100
# 피보나치 함수를 재귀함수로 구현(탑다운)
def fibo(x):
# 종료 조건
if x == 1 or x == 2:
return 1
# 이미 계산한 문제 그대로 반환
if d[x] != 0:
return d[x]
# 아직 계산하지 않은 문제
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
print(fibo(99))
- 보텀업 방식
# 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
d = [0] * 100
# 첫 번째 피보나치 수와 두 번째 피보나치 수는 1
d[1] = 1
d[2] = 1
n = 99
# 피보나치 함수 반복문으로 구현(보텀업)
for i in range(3, n+1):
d[i] = d[i-1] + d[i-2]
print(d[n])메모이제이션 동작 분석
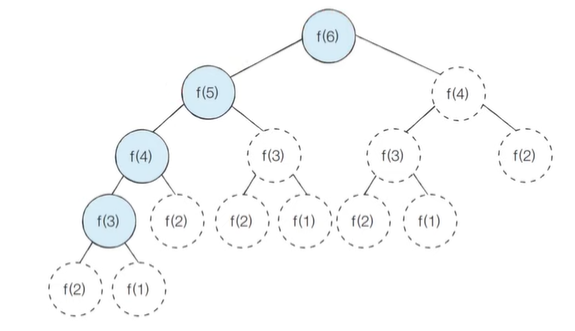
d = [0] * 100
def fibo(x):
print('f(' + str(x) + ')', end=' ')
if x == 1 or x == 2:
return 1
if d[x] != 0:
return d[x]
d[x] = fibo(x-1) + fibo(x-2)
return d[x]
fibo(6)
실행결과
f(6) f(5) f(4) f(3) f(2) f(1) f(2) f(3) f(4)
이렇게 메모이제이션을 이용하면 N의 값이 아무리 커진다고 해도 메모리 공간 또한 N만큼 가질 수 있다면 충분히 선형시간 알고리즘(O(N))으로 피보나치 수열을 해결할 수 있다.
다이나믹 프로그래밍 vs 분할 정복
둘 모두 최적 부분 구조를 가질 때 사용할 수 있다. 차이점은 부분 문제의 중복이다. 다이나믹 프로그래밍은 각 부분 문제들이 서로 영향을 미치면 부분 문제가 중복되지만 Quick 정렬같은 분할 정복 문제는 동일한 부분 문제가 반복적으로 계산되지 않는다.
퀵 정렬은 한 번 기준 원소(Pivot)가 자리를 변경해서 자리를 잡으면 그 기준 원소의 위치는 바뀌지 않는다. 분할 이후에 해당 피벗을 다시 처리하는 부분 문제는 호출하지 않는다.
다이나믹 프로그래밍 문제에 접근하는 방법
주어진 문제가 다이나믹 프로그래밍 유형임을 파악하는 것이 중요하다.
1. 가장 먼저 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는지 검토하고 떠오르지 않으면 다이나믹을 고려한다.
2. 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성한 뒤에 (탑다운) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 코드를 개선하는 방법을 사용할 수 있다.
<문제> 개미 전사
메뚜기 마을에의 식량창고들은 일직선으로 이어져 있다. 각 식량창고에는 정해진 수의 식량을 저장하고 있으며 개미 전사는 식량창고를 선택적으로 약탈하여 식량을 빼앗는다. 이때 메뚜기 정찰병들은 일직선상에 존재하는 식량창고 중에서 서로 인접한 식량창고가 공격받으면 바로 알아챈다. 따라서 개미 전사가 정찰병에게 들키지 않고 식량창고를 약탈하기 위해선 최소 한 칸 이상 떨어진 식량창고를 약탈해야 한다.
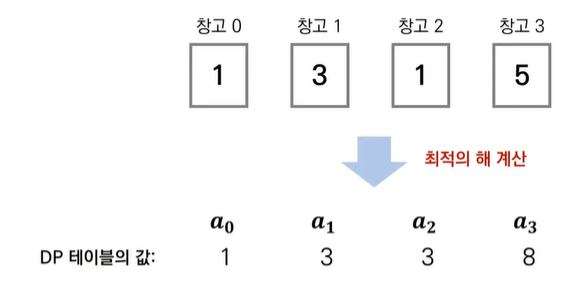
예를 들어 식량창고가 {1, 3, 1, 5}라면 3, 5를 털어서 최댓값이 총 8개의 식량을 빼앗을 수 있는 것이다. 개미 전사가 식량창고 N개에 대한 정보가 주어졌을 때 얻을 수 있는 식량의 최댓값을 구하는 프로그램을 작성하시오
[해결 아이디어]
N=4일 때, 8가지 경우의 수가 존재한다.

ai = i번째 식량창고까지의 최적의 해라고 했을 경우 다이나믹 프로그래밍을 적용할 수 있다.
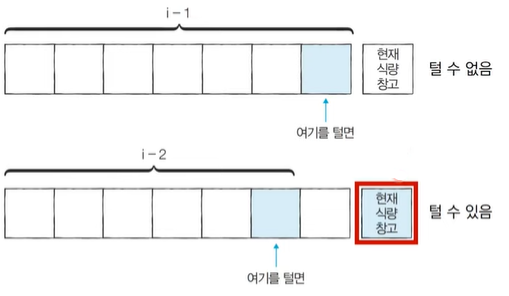
왼쪽부터 식량창고를 턴다고 했을 때, 특정한 i번째 식량창고를 털지의 여부를 결정하려면 아래 2가지 경우 중에서 더 많은 식량을 털 수 있는 경우를 선택하면 된다.
조건 확인하기
최적 부분 구조 : 특정 번째까지의 최적의 해는 i-1, i-2번째까지의 최적의 해를 이용해서 계산될 수 있다.
ki를 i번째 식량창고에 있는 식량의 양이라고 했을 때 ai의 점화식은 다음과 같다.
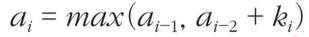
N = int(input())
array = list(map(int, input().split()))
d = [0] * 100
d[0] = array[0]
d[1] = max(array[0], array[1])
for i in range(2, n):
d[i] = max(d[i-1], d[i-2] + array[i])
print(d[n-1])<문제> 1로 만들기
정수 X가 주어졌을 때,
1. X가 5로 나누어 떨어지면, 5로 나눈다.
2. X가 3으로 나누어 떨어지면, 3으로 나눈다.
3. X가 2로 나누어 떨어지면, 2로 나눈다.
4. X에서 1을 뺀다.
정수 X가 주어졌을 때, 연산 4개를 적절히 사용해서 값을 1로 만들고자 한다. 연산을 사용하는 횟수의 최솟값을 출력해보자.
ex) 26 -> 25 -> 5 -> 1
f(6)의 경우 f(5), f(3), f(2)의 해로 구할 수 있고 f(1)과 f(2) 같은 값이 중복되기 때문에 최적 부분 구조와 중복되는 부분 문제를 만족한다.
- 점화식
# 정수 x 입력 받기
x = int(input())
# DP 테이블
d = [0] * 30001
# 다이나믹 프로그래밍 (보텀업)
for i in range(2, x + 1):
# 1을 빼는 경우
d[i] = d[i - 1] + 1
# 2로 나누어 떨어지는 경우
if i % 2 == 0:
d[i] = min(d[i], d[i//2] + 1)
# 3로 나누어 떨어지는 경우
if i % 3 == 0:
d[i] = min(d[i], d[i//3] + 1)
# 5로 나누어 떨어지는 경우
if i % 5 == 0:
d[i] = min(d[i], d[i//5] + 1)
print(d[x])<문제> 효율적인 화폐 구성
N가지 종류의 화폐가 있다. 화폐의 개수를 최소한으로 이용하여 합이 M원이 되도록 한다.
ex) 2원, 3원 단위 화폐가 있을 때 15원 만들기 위해선 3원 5개가 최소 개수
조건 확인하기: 최적 부분 구조, 중복 부분 구조 만족.
[입출력 조건]
첫째 줄에 N, M. 이후의 N개의 줄에서 각 화폐의 단위 주어진다. (1 <= N <= 100, 1 <= M <= 10,000) 출력이 불가능할 경우 -1 출력.
[해결 아이디어]

먼저 각 인덱스에 해당하는 값으로 INF(무한)의 값을 설정한다. 첫 번째 단위부터 확인하면서 리스트를 새로 갱신해준다.
# N, M 입력 받기
n, m = map(int, input().split())
# N개의 줄에서 화폐 단위 받기
array = []
for i in range(n):
array.append(int(input()))
# DP 테이블
d = [10001] * (m+1)
d[0] = 0
for i in range(n):
for j in range(array[i], m+1):
if d[j - array[i]] != 10001: # (i - k)원을 만드는 방법이 존재하는 경우
d[j] = min(d[j], d[j - array[i]] + 1)
# 계산된 결과 출력
if d[m] == 10001:
print(-1)
else:
print(d[m])
<문제> 금광
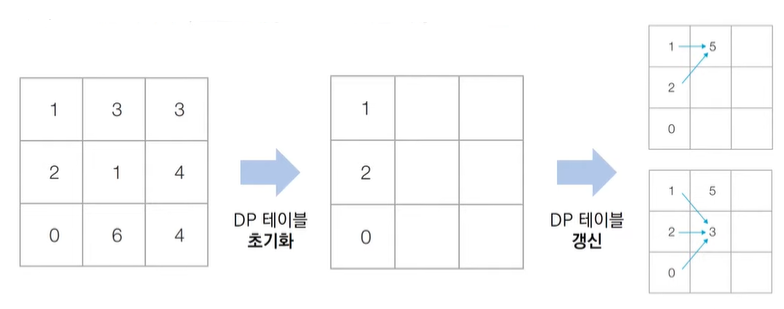
n x m 크기의 금광. 각 칸은 특정한 크기의 금이 들어있다. 채굴자는 첫 번째 열부터 출발하여 금을 캔다. 처음 첫 번째 열의 어느 행에서든 출발할 수 있다. 이후에 m-1번에 걸쳐서 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해서 금을 캔다. 결과적으로 채굴자가 얻을 수 있는 금의 최대 크기를 출력하는 프로그램을 작성하시오.
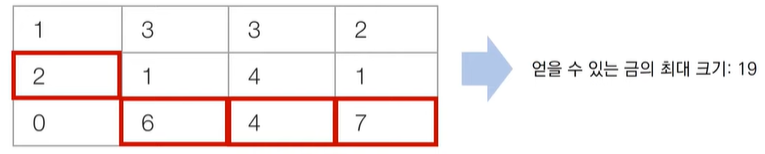
[해결 아이디어]
금강의 모든 위치에서 3가지만 고려하면 된다.
1. 왼쪽 위에서 오는 경우
2. 왼쪽 아래에서 오는 경우
3. 왼쪽에서 오는 경우
3가지 경우 중 가장 많은 금을 가지고 있는 경우를 테이블에 갱신해준다.

이 때 리스트의 범위를 벗어나지 않는지 체크해주어야 한다.
# 테스트 케이스 (Test Case) 입력
for tc in range(int(input())):
# 금광 정보 입력
n, m = map(int, input().split())
array = list(map(int, input().split()))
# 다이나믹 프로그래밍을 위한 2차원 DP 테이블 초기화
dp = []
index = 0
for i in range(n):
dp.append(array[index:index + m])
index += m
# 다이나믹 프로그래밍 진행
for j in range(1, m):
for i in range(n):
# 왼쪽 위에서 오는 경우
if i == 0:
left_up = 0
else:
left_up = dp[i - 1][j - 1]
# 왼쪽 아래에서 오는 경우
if i == n - 1:
left_down = 0
else:
left_down = dp[i + 1][j - 1]
# 왼쪽에서 오는 경우
left = dp[i][j - 1]
dp[i][j] = dp[i][j] + max(left_up, left_down, left)
result = 0
for i in range(n):
result = max(result, dp[i][m - 1])
print(result)
<문제> 병사 배치하기
- N명의 병사가 무작위로 나열. 각 병사는 특정한 값의 전투력 보유.
- 병사를 배치할 때는 전투력이 높은 병사가 앞쪽에 오도록 내림차순 배치
- 특정한 위치에 있는 병사를 열외하는 방법으로 배치. 그러면서도 남아 있는 병사의 수가 최대가 되도록.
[해결아이디어]
가장 긴 증가하는 부분 수열(Longest Increasing Subsequence, LIS)로 전형적인 다이나믹 프로그래밍 문제의 아이디어이다.
array = {4,2,5,8,4,11,15}가 있을 때 이 수열의 가장 긴 증가하는 부분 수열은 {4,5,8,11,15}이다.
본 문제는 가장 긴 감소하는 부분 수열을 찾는 문제로 치환할 수 있으므로, LIS 알고리즘을 조금 수정하여 적용함으로써 정답을 도출한다.
LIS 알고리즘
가장 먼저 입력 받은 병사 정보의 순서를 뒤집은 후 가장 긴 증가하는 부분 수열(LIS) 알고리즘을 수행하면 된다.
n = int(input())
array = list(map(int, input().split()))
# 순서를 뒤집어 LIS 문제로 변환
array.reverse()
# 1차원 DP 테이블 초기화
dp = [1] * n
# LIS 알고리즘 수행
for i in range(1, n):
for j in range(0, i):
if array[j] < array[i]:
dp[i] = max(dp[i], dp[j] + 1)
print(dp)
# 열외해야 하는 병사의 최소 수 출력
print(n - max(dp))


