최소 공통 조상(Lowest Common Ancestor): 기초 문제

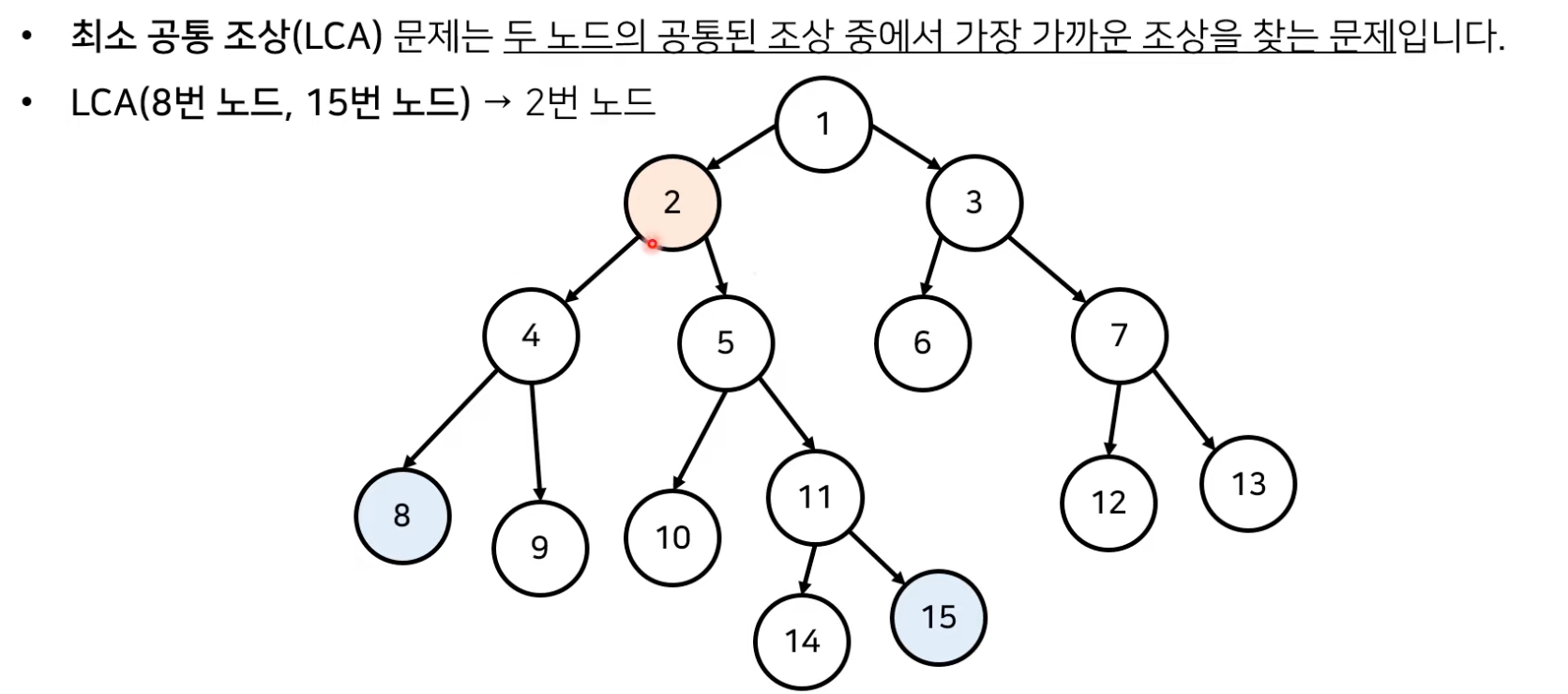
기본적인 최소 공통 조상(LCA) 알고리즘
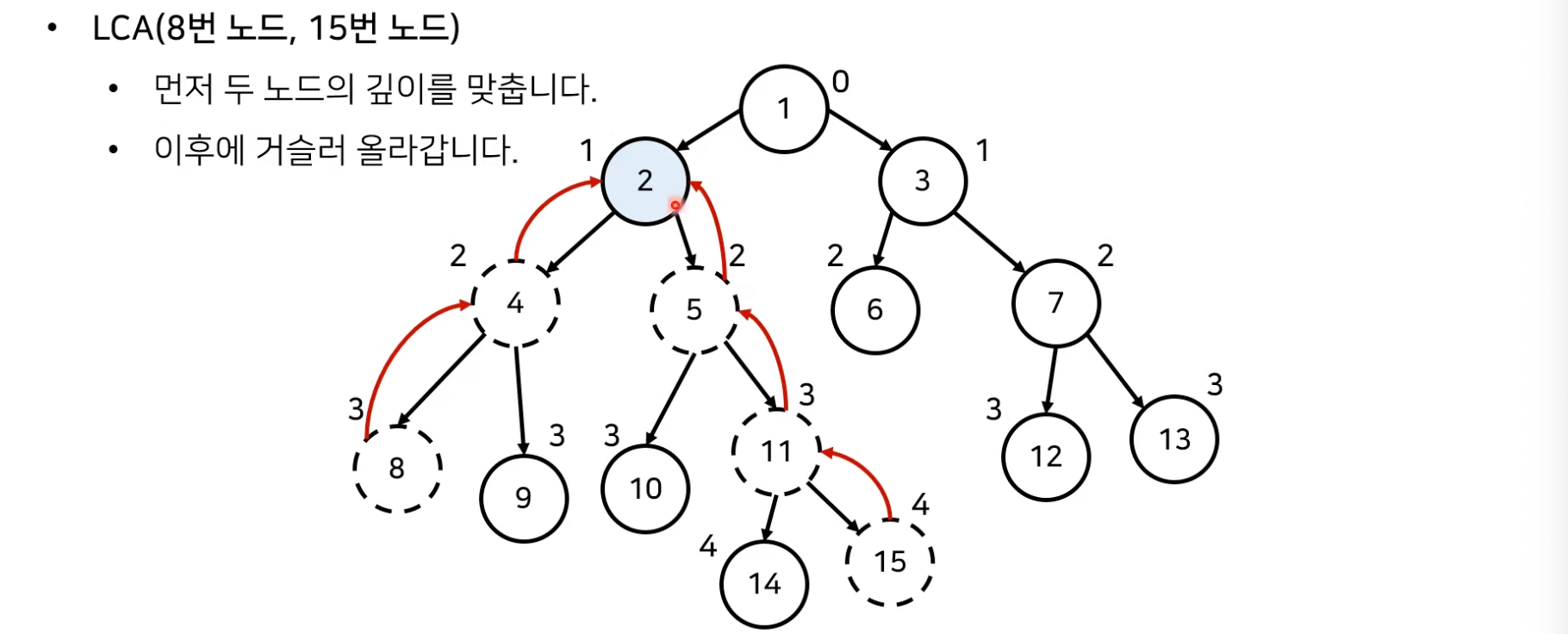
- 최소 공통 조상 찾기 알고리즘은 다음과 같다.

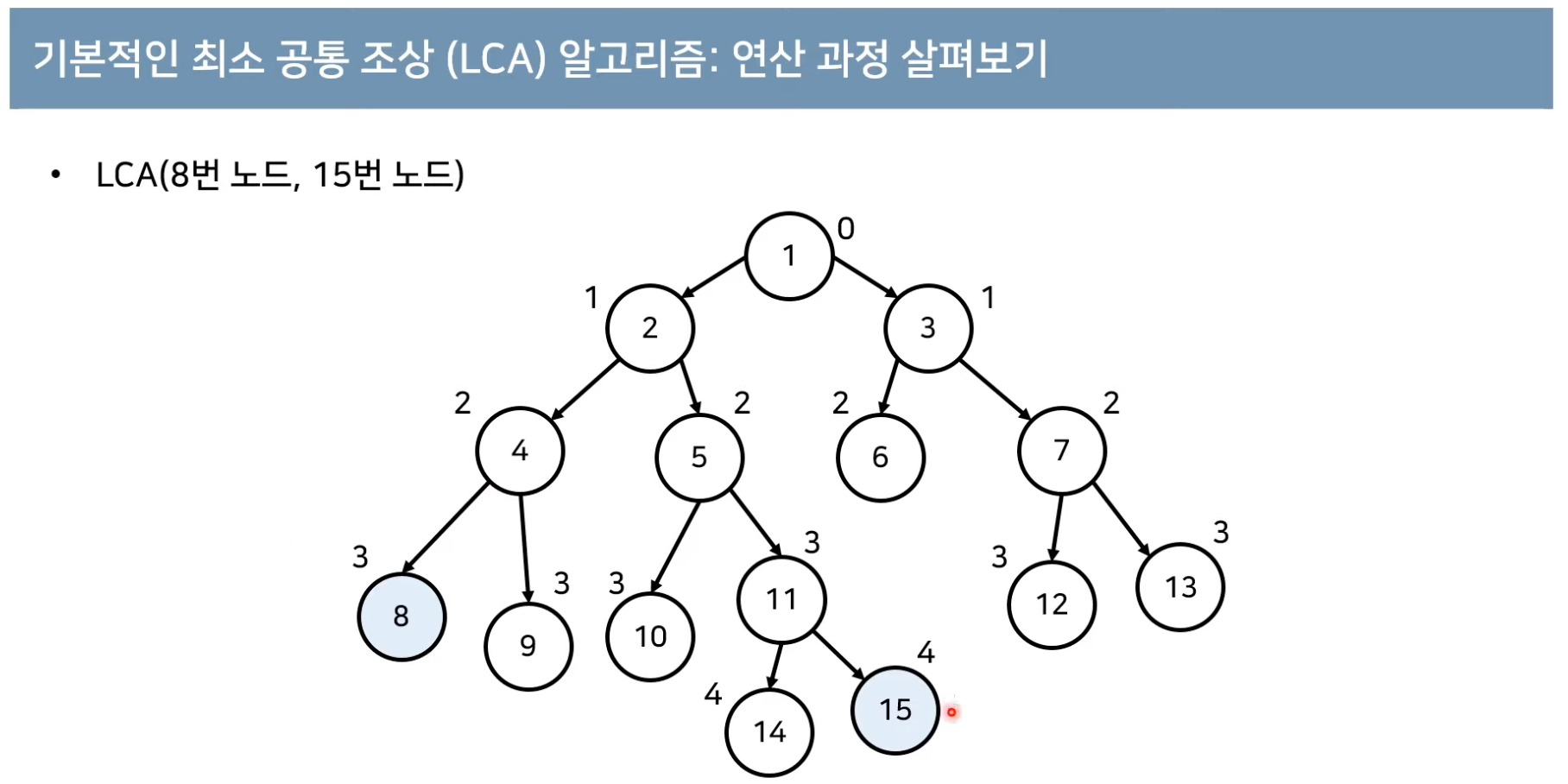
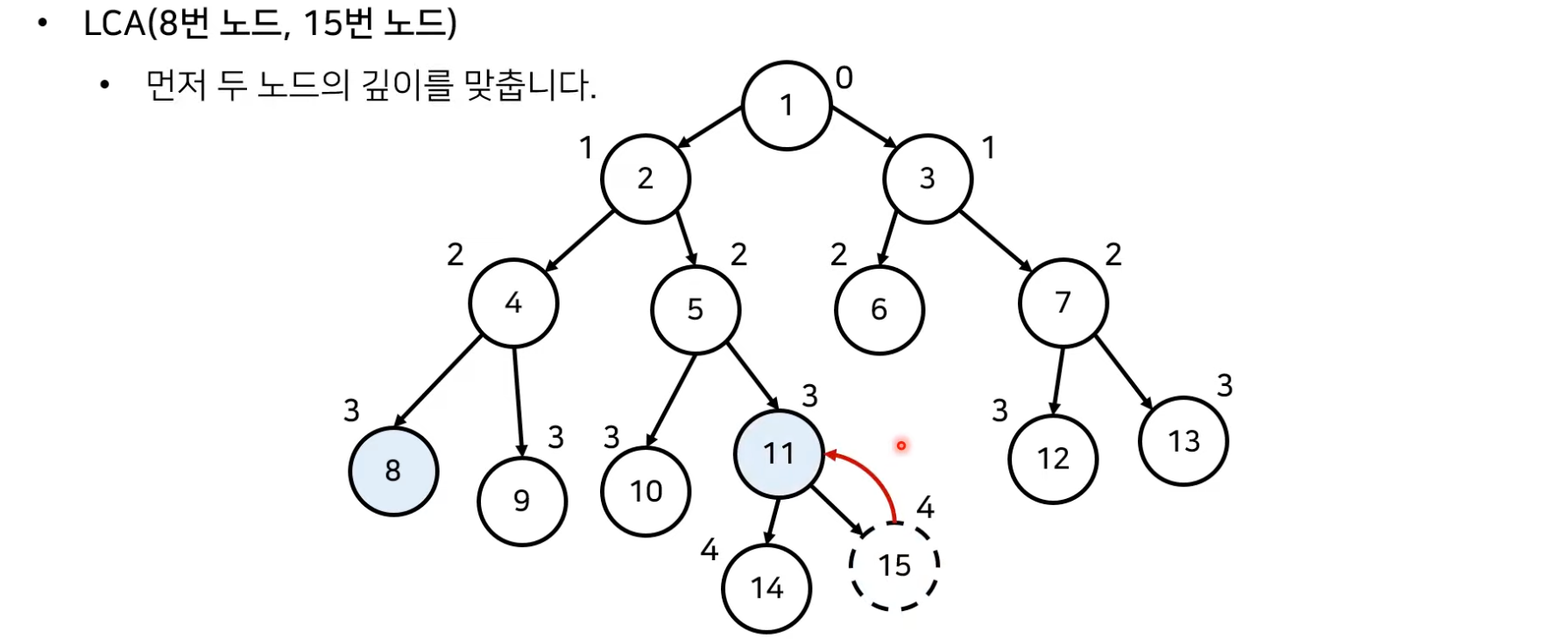
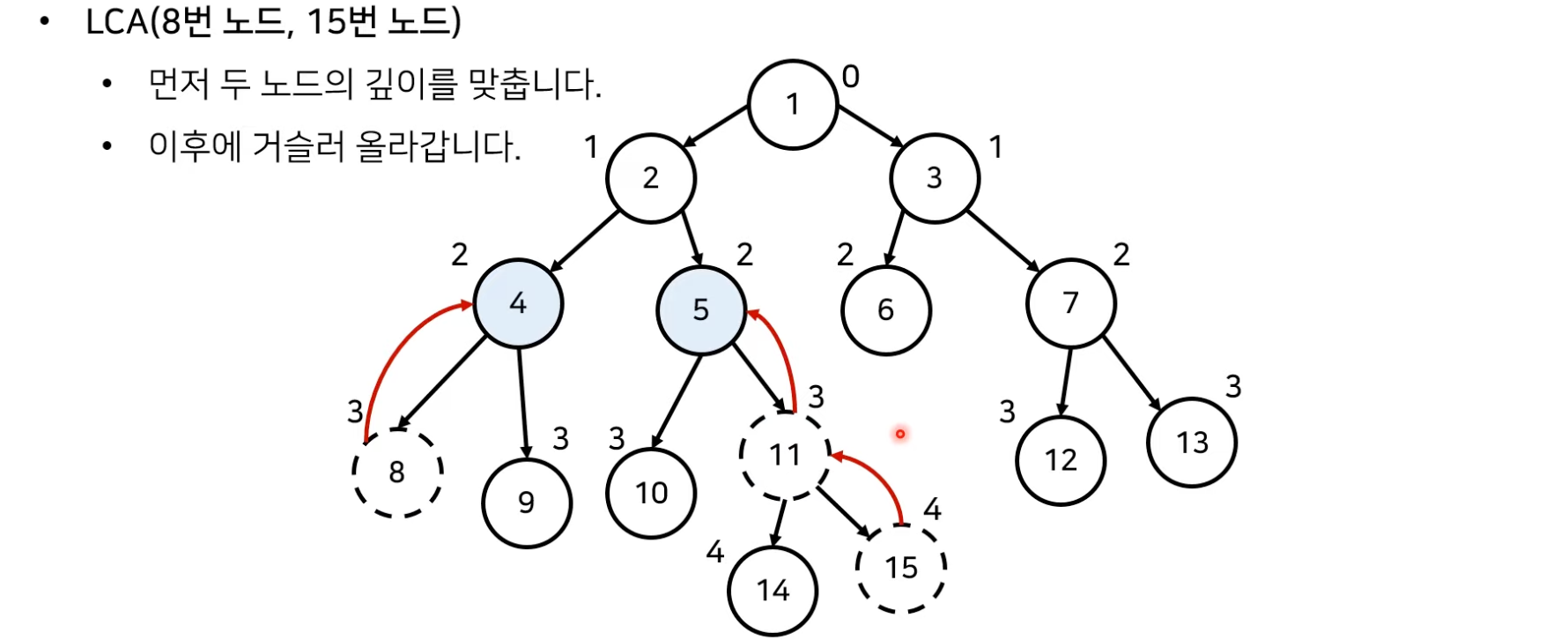
import sys
sys.setrecursionlimit(int(1e5))
n = int(input())
parent = [0] * (n + 1)
d = [0] * (n + 1)
c = [0] * (n + 1)
graph = [[] for _ in range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().spli())
graph[a].append[b]
graph[b].append[a]
def dfs(x, depth):
c[x] = True
d[x] = depth
for y in graph[x]:
if c[y]:
continue
parent[y] = x
dfs(y, depth + 1)
def lca(a, b):
while d[a] != d[b]:
if d[a] > d[b]:
a = parent[a]
else:
b = parent[b]
while a != b:
a = parent[a]
b = parent[b]
return a
dfs(1, 0)
m = int(input())
for i in range(m):
a, b = map(int, input().split())
print(lca(a, b))

최소 공통 조상(Lowest Common Ancestor): 심화 문제


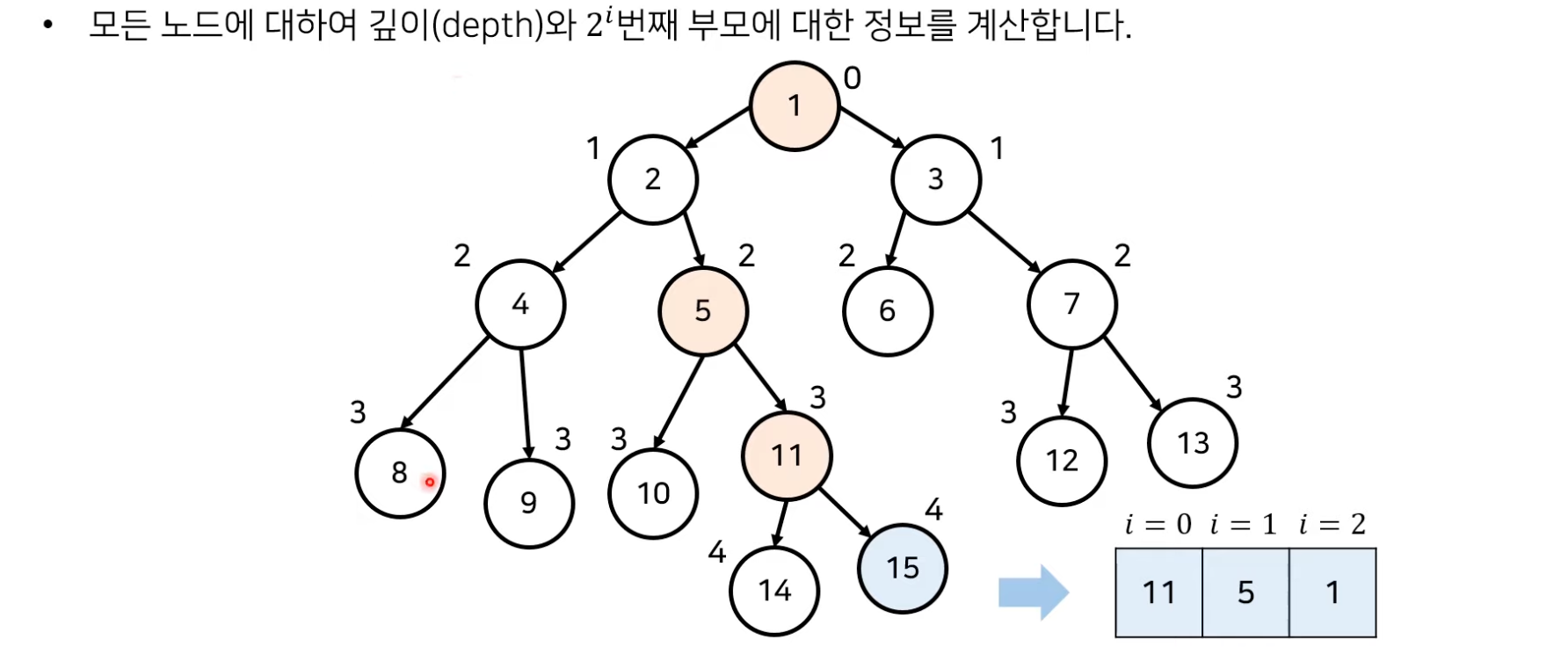
개선된 최소 공통 조상(LCA) 알고리즘: 모든 노드의 깊이와 부모 구하기
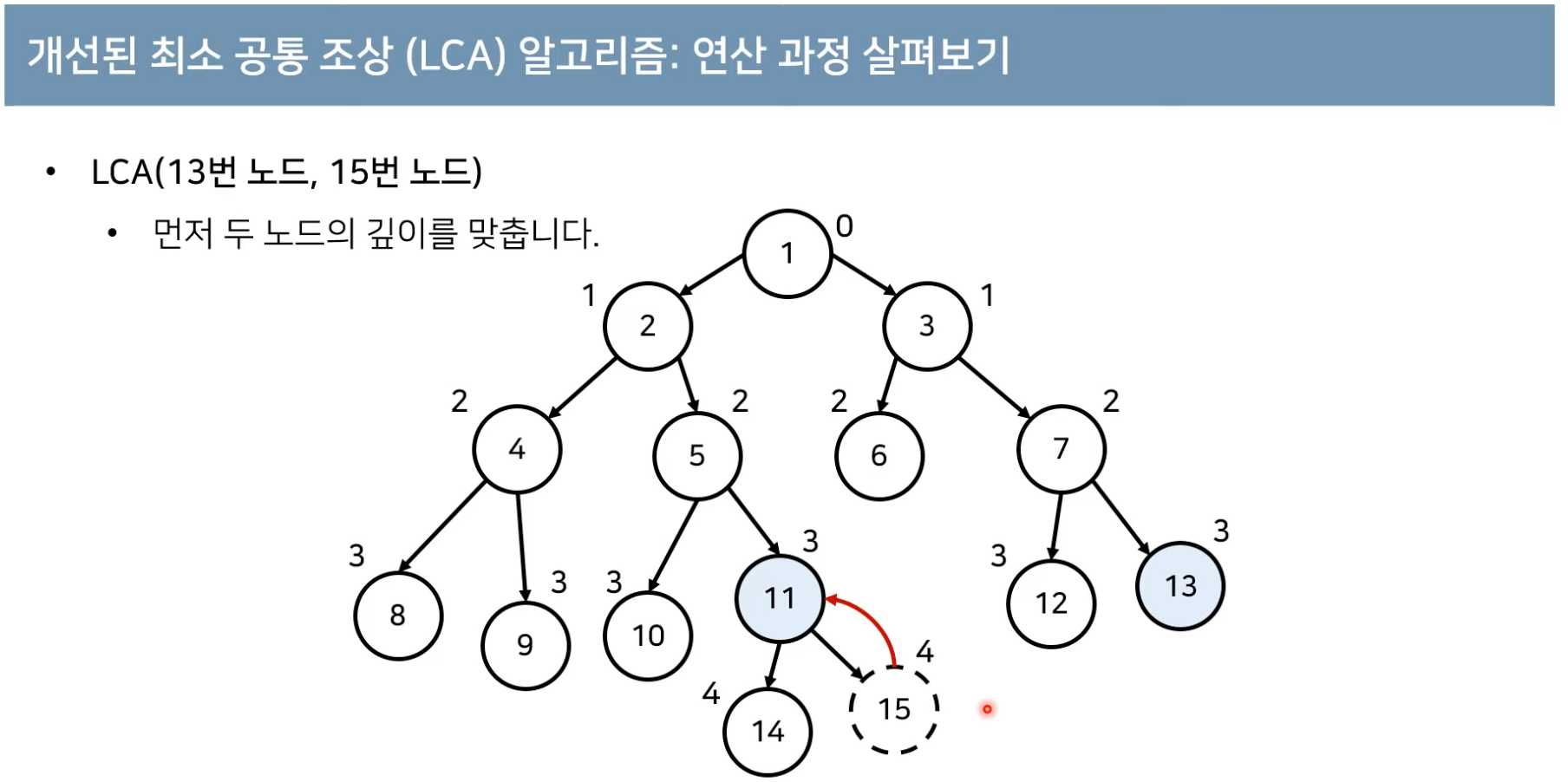
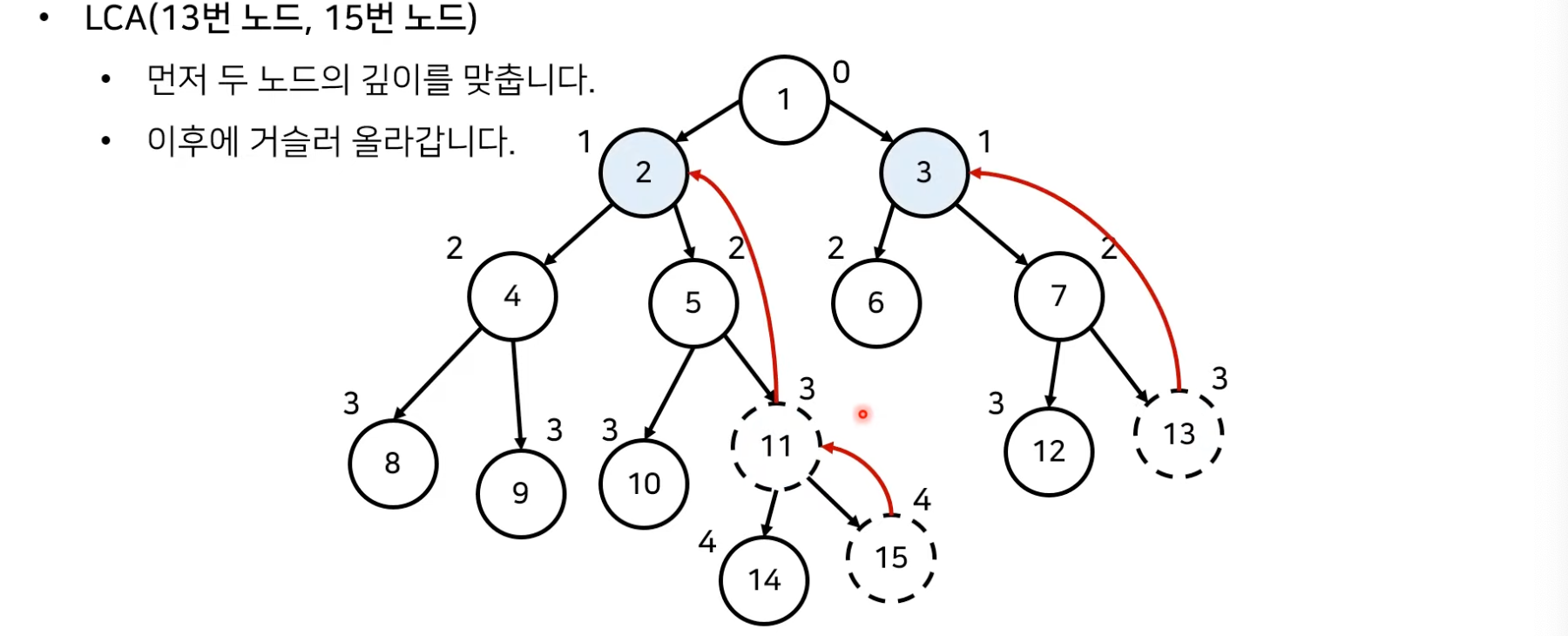
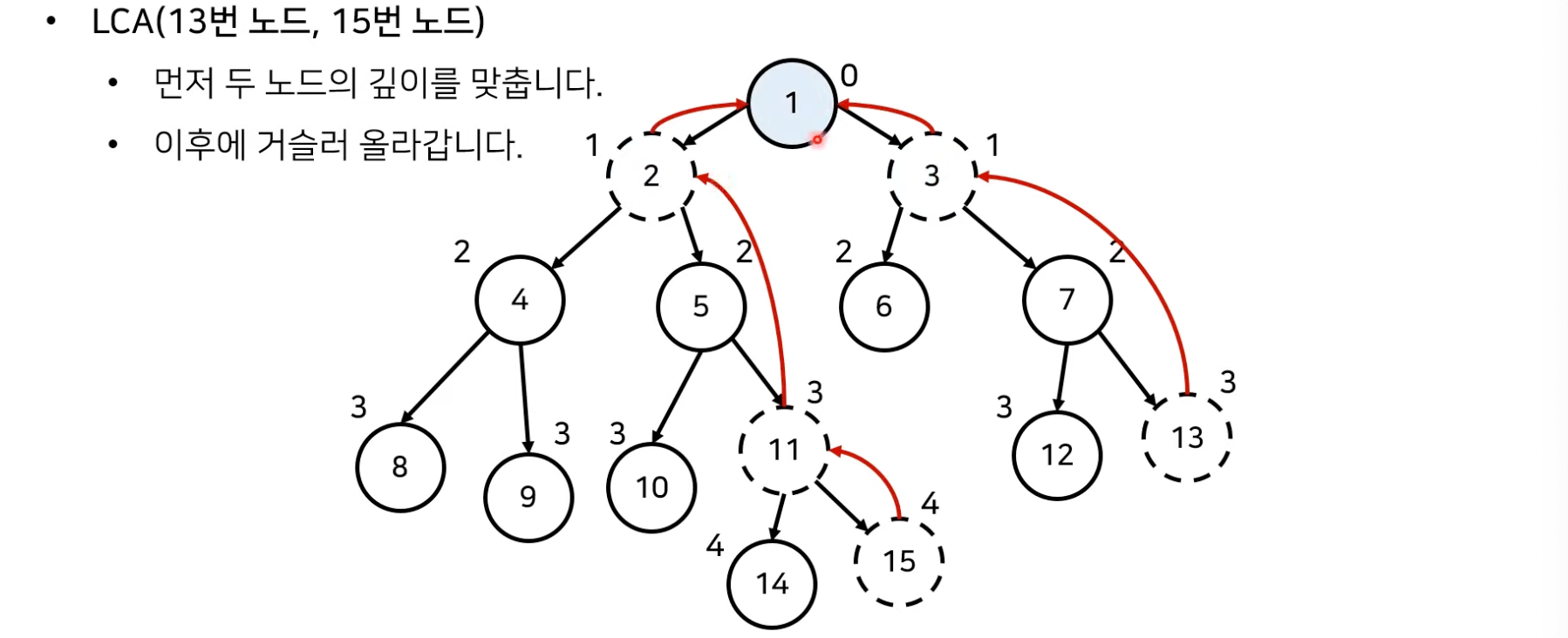

- 위의 방법은 코드로 구현하지 않는 단계에서 학습 종료















