[JavaScript] Heap 구현하기

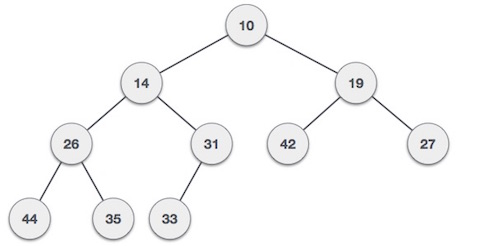
Heap(Heap Tree)이란?

• 여러 개의 값 중에서 가장 작은 값을(최대 힙의 경우는 큰 값) 빠르게 찾기 위해 만든 완전 이진 트리.
• 트리의 부모 노드는 자식 노드보다 항상 작은 값(최대 힙의 경우는 큰 값)을 가진다.
• 짧게 힙(Heap)이라고 줄여서 부르기도 한다.
• 우선 순위 큐를 구현하는 데에 사용된다.

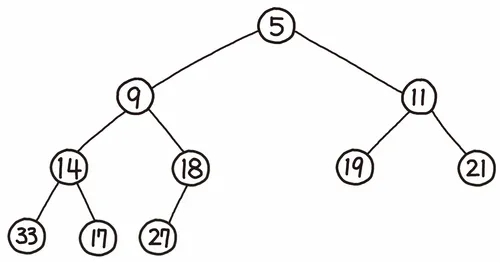
이미지 출처: 나무위키

Heap의 데이터 삽입과 삭제

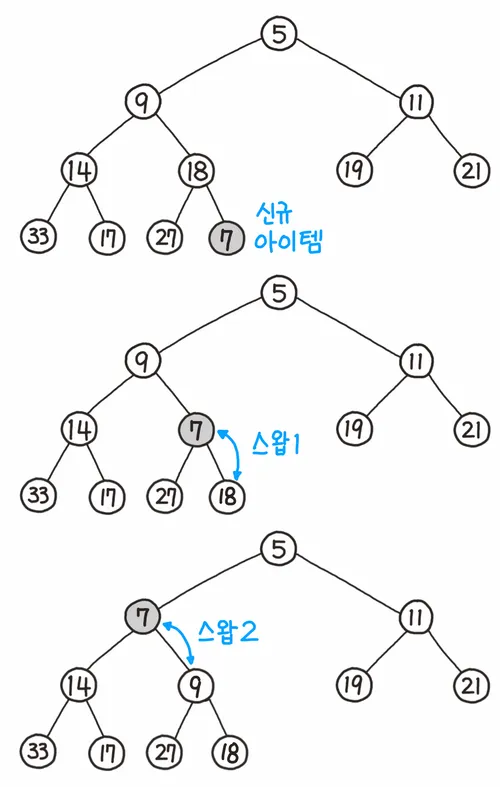
데이터 삽입

1. 트리의 가장 끝에 노드를 삽입한다.
2. 해당 노드와 부모 노드를 비교하여 규칙에 맞도록 교환한다.
3. Heap의 규칙에 맞을 때까지 2번을 반복한다. (Bubble Up)

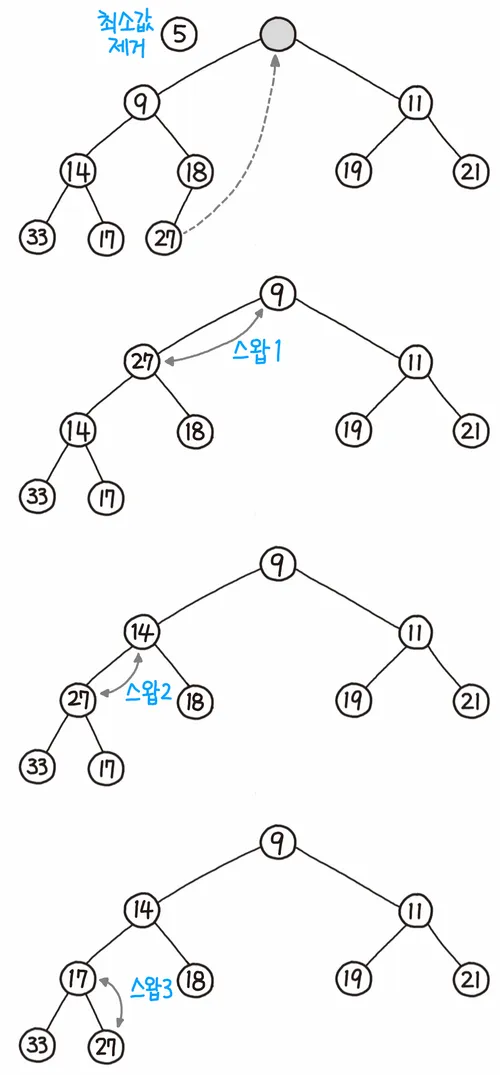
데이터 삭제

1. 루트 노드를 삭제한다.
2. 트리 가장 끝의 노드를 루트에 위치시킨다.
3. 해당 노드와 자식 노드를 비교하여 규칙에 맞도록 교환한다.
4. Heap의 규칙에 맞을 때까지 3번을 반복한다. (Bubble Down)

JavaScript의 Heap

C++, Python 등의 언어에는 Heap(또는 우선 순위 큐)를 간편하게 사용할 수 있는 라이브러리 등이 있지만, JavaScript에는 없다...
그래서 최소,최대 Heap을 직접 구현하여 사용해야 한다.
아래는 Class로 구현한 Heap이다.

주석 참고

class Heap {
    // 최소, 최대 Heap 구분
    constructor(isMinHeap = true) {
        this.heap = [];
        // Heap의 종류에 따라 다른 비교 연산
        this.compare = isMinHeap ? (a, b) => a - b : (a, b) => b - a;
    }
    
    // 노드 교환
    swap(index1, index2) {
        [this.heap[index1], this.heap[index2]] = [this.heap[index2], this.heap[index1]];
    }
    
  	// 데이터 삽입
  	insert(value) {
        this.heap.push(value);
      	// 데이터 삽입 후 Heap 규칙에 맞게 정리
        this.bubbleUp();
    }
    bubbleUp() {
      	// 트리 끝의 노드
        let index = this.heap.length - 1;
        while(index > 0) {
          	// 비교할 부모 노드
            const parentIndex = Math.floor((index - 1) / 2);
            // 현재 노드의 값이 부모 노드의 값보다 크면(최대힙은 작으면) 끝
            if(this.compare(this.heap[parentIndex], this.heap[index]) <= 0) break;
            // 규칙에 맞지 않으면 두 노드를 교환
            this.swap(parentIndex, index);
          	// 다음 bubbleUp연산을 위해 교환한 자리의 index를 할당
            index = parentIndex;
        }
    }
    
    // 데이터 삭제
  	remove() {
      	// 트리가 비어있으면 null 반환
        if(this.heap.length === 0) return null;
      	// 트리에 노드가 하나이면 바로 삭제 및 반환
        if(this.heap.length === 1) return this.heap.pop();
        
        const root = this.heap[0];
      	// 트리 가장 끝의 노드를 루트로 이동
        this.heap[0] = this.heap.pop();
      	// 이동 후 Heap 규칙에 맞게 정리
        this.bubbleDown();
      	// 삭제한 데이터 반환
        return root;
    }
    bubbleDown() {
      	// 루트(로 이동한) 노드
        let index = 0;
        const length = this.heap.length;
      	// 노드가 리프로 갈 때까지 반복
        while(index * 2 + 1 < length) {
            let betterIndex = index * 2 + 1;
            const rightIndex = index * 2 + 2;
          	// 오른쪽 자식이 존재할 때, 양쪽 자식 노드 중 작은(최대 힙은 큰) 값을 선택
            if(rightIndex < length && this.compare(this.heap[rightIndex], this.heap[betterIndex]) < 0) {
                betterIndex = rightIndex;
            }
            // 현재 노드의 값이 자식 노드의 값보다 작으면(최대 힙은 크면) 끝
            if(this.compare(this.heap[index], this.heap[betterIndex]) <= 0) break;
            // 규칙에 맞지 않으면 두 노드를 교환
            this.swap(index, betterIndex);
          	// 다음 bubbleDown연산을 위해 교환한 자리의 index를 할당
            index = betterIndex;
        }
    }
}

// 사용 예시
const arr = [1, 2, 3, 4, 5];
const maxHeap = new Heap(false);

arr.forEach(el => maxHeap.insert(el));
arr.remove();