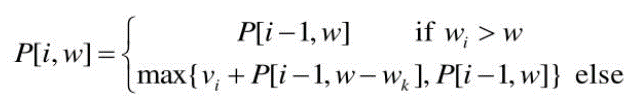12865: 평범한 배낭 && 12920: 평범한 배낭 2

12865: 평범한 배낭

• 0-1 knapsack 문제이다. fractional kanpsack 문제는 greedy로 풀 수 있지만, 0-1 knapsack 문제는 dynamic programming으로 풀어야함
• 이 문제의 점화식은 아래와 같다
  
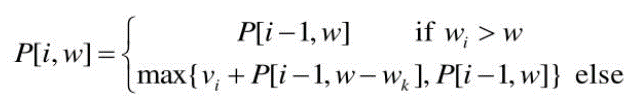
• dp 테이블의 값 (dp[i, weight])은 i개의 물건이 있고, 배낭의 무게한도가 weight일 때 최대의 가치합을 의미함
• i번째 물건이 배낭의 무게 한도보다 무거우면 i번째 물건을 뺀 i-1개의 물건들을 가지고 구한 전 단계의 최적값을 그대로 가져옴
• 그렇지 않은 경우, "i번째 물건을 위해 i번째 물건만큼의 무게를 비웠을 때의 최적값에 i번째 물건의 가격을 더하 값"과 "i-1개의 물건들을 가지고 구한 전 단계의 최적값" 중 큰 값을 할당함

import sys

N, W = map(int, input().split())
wt = []; val = []
for _ in range(N):
    tmp = list(map(int, sys.stdin.readline()[:-1].split()))
    wt.append(tmp[0]); val.append(tmp[1])

dp = [[0 for _ in range(W+1)] for __ in range(N+1)]
for i in range(N+1):
    for weight in range(W+1):
        if i == 0 or weight == 0:
            dp[i][weight] = 0
        elif wt[i-1] <= weight:
            dp[i][weight] = max(val[i-1] + dp[i-1][weight-wt[i-1]], dp[i-1][weight])
        else:
            dp[i][weight] = dp[i-1][weight]
# print(dp)
print(dp[N][W])

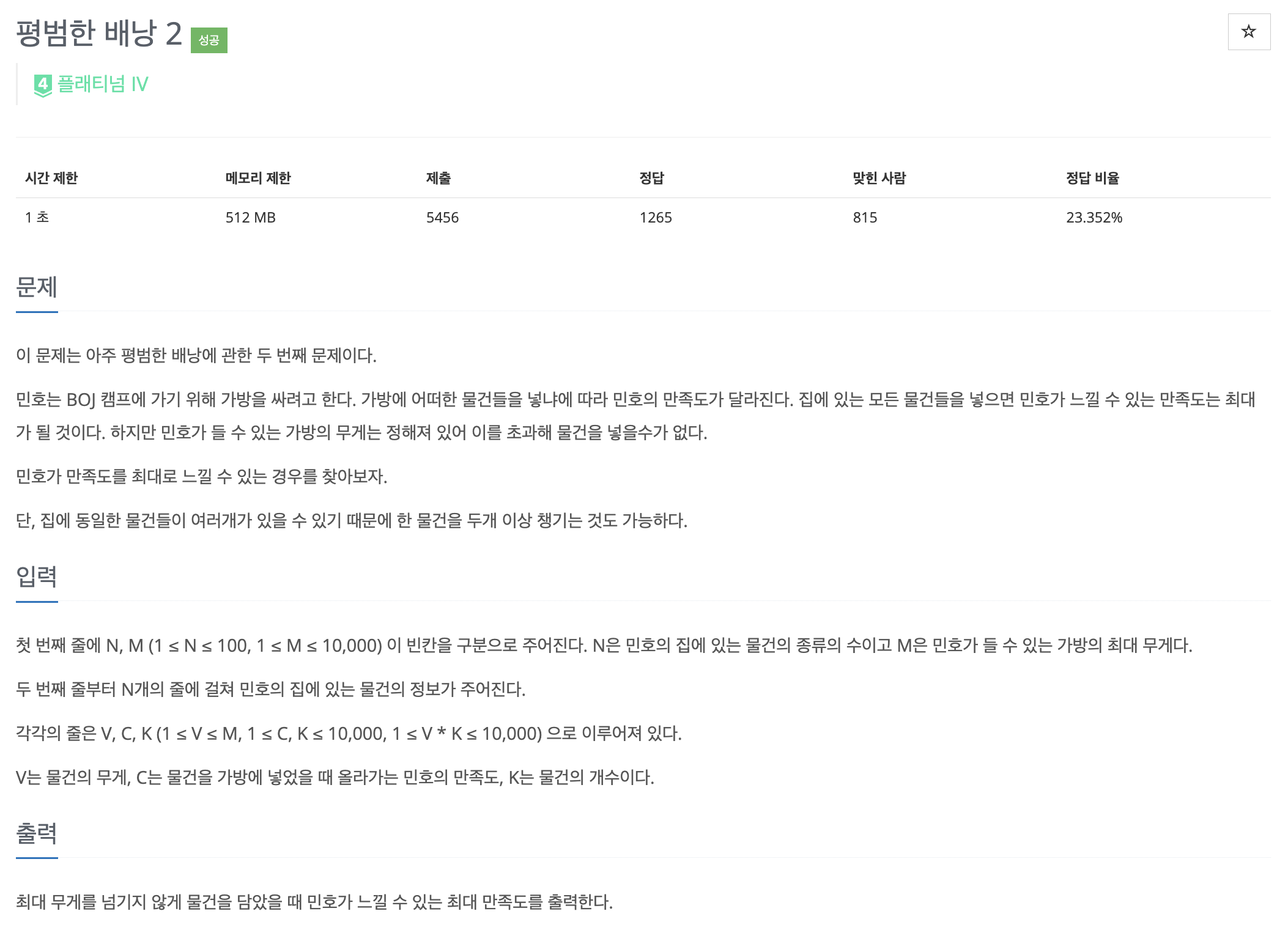
12920: 평범한 배낭 2

import sys

N, W = map(int, input().split())
wt = []; val = []
for _ in range(N):
    tmp = list(map(int, sys.stdin.readline()[:-1].split()))
    for __ in range(tmp[2]):
        wt.append(tmp[0]); val.append(tmp[1])

dp = [[0 for _ in range(W+1)] for __ in range(len(val)+1)]
for i in range(len(val)+1):
    for weight in range(W+1):
        if i == 0 or weight == 0:
            dp[i][weight] = 0
        elif wt[i-1] <= weight:
            dp[i][weight] = max(val[i-1] + dp[i-1][weight-wt[i-1]], dp[i-1][weight])
        else:
            dp[i][weight] = dp[i-1][weight]
# print(dp)
print(dp[len(val)][W])

• 메모리 초과 발생
• 공간 복잡도를 줄이기 위해, 비트마스킹을 이용하여 수를 표현해야함 (모든 수는 2의 제곱수들의 합으로 표현 가능)

idx = 1 #2의 제곱수
    while K > 0:
        tmp = min(idx, K) #K를 2의 제곱수의 합으로 표현하기 위해 (ex 5 = 1 + 2 + 2)
        weight.append(V * tmp)
        value.append(C * tmp)
        idx *= 2
        K -= tmp #이미 계산한 2의 제곱수는 K에서 빼줘야함

• 예를 들어 15개의 물건이 있다면, 15 = 1 + 2 + 4 + 8이기 때문에 1개, 2개, 4개, 8개 씩 더해주는 경우와 같음
• dp table을 1차원 리스트로 선언함

dp = [0 for _ in range(W + 1)]
for i in range(len(weight)):
    for j in range(W, 0, -1):
        if j >= weight[i]:
            dp[j] = max(dp[j], dp[j-weight[i]] + value[i])

• j만큼의 무게를 들 수 있을 때, weight 리스트의 i번째에 해당하는 물건을 넣을 수 있다면 dp[j]를 갱신
• dp[j]의 값과 "dp[현재 들 수 있는 최대 무게 - i번째 물건의 무게] + i번째 물건의 만족도" 중 큰 값으로 갱신해야함

정답 코드

import sys

N, W = map(int, input().split())
weight = []; value = []
for _ in range(N):
    V, C, K = map(int, sys.stdin.readline()[:-1].split()) #V는 물건의 무게, C는 물건의 가치, K는 물건의 개수

    idx = 1 #2의 제곱수
    while K > 0:
        tmp = min(idx, K) #K를 2의 제곱수의 합으로 표현하기 위해 (ex 5 = 1 + 2 + 2)
        weight.append(V * tmp)
        value.append(C * tmp)
        idx *= 2
        K -= tmp #이미 계산한 2의 제곱수는 K에서 빼줘야함

dp = [0 for _ in range(W + 1)]
for i in range(len(weight)):
    for j in range(W, 0, -1):
        if j >= weight[i]:
            dp[j] = max(dp[j], dp[j-weight[i]] + value[i])
print(dp[-1])

• 플레 문제는 확실히 다른 것 같다 깨갱