2749: 피보나치 수 3 && 11444: 피보나치 수 6

2749: 피보나치 수 3

• "피사노 주기"를 이용함
• 피사노 주기는 N번째 피보나치 수를 M으로 나눈 나머지는 N % P번째 피보나치 수를 M으로 나눈 나머지와 같다는 원리
• M = 10^k 일 때, k > 2라면, 주기는 항상 15*10^(k-1)임

import sys

N = int(sys.stdin.readline()[:-1])
M = 1000000 #10의 7승 (나누는 수)
P = 15*(10**(6-1)) #주기의 길이

fibo = [0, 1]
for i in range(2, P): #주기의 길이만큼만 fibo를 만듦
    fibo.append(fibo[i-1] + fibo[i-2])
    fibo[i] %= M

print(fibo[N%P])

11444: 피보나치 수 6

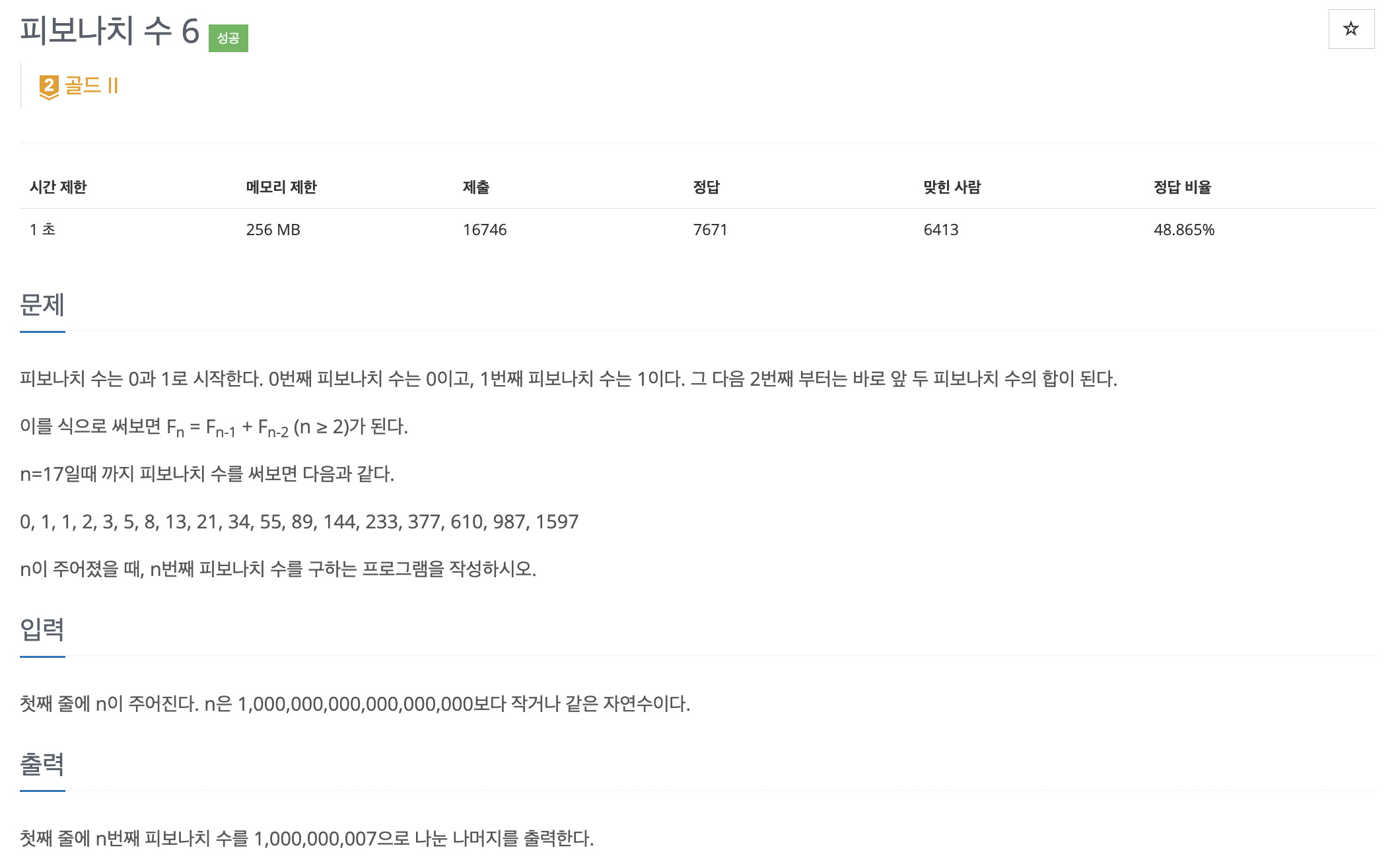
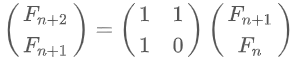
• 분할정복을 이용한 행렬의 거듭제곱을 사용하여 큰 수의 피보나치를 구할 수 있다

import sys

def multi(mat1, mat2):
    result = [[0] * 2 for _ in range(2)]
    for i in range(2):
        for j in range(2):
            for z in range(2):
                result[i][j] += mat1[i][z] * mat2[z][j] % 1000000007
    return result

def recursion(a, b):
    if b == 1:
        return a
    else:
        tmp = recursion(a, b // 2)
        if b % 2 == 0:
            return multi(tmp, tmp)
        else:
            return multi(multi(tmp, tmp), a)

N = int(sys.stdin.readline()[:-1])
matrix = [[1, 1], [1, 0]]
result = recursion(matrix, N)
print(result[0][1] % 1000000007)