4485: 녹색 옷 입은 애가 젤다지?

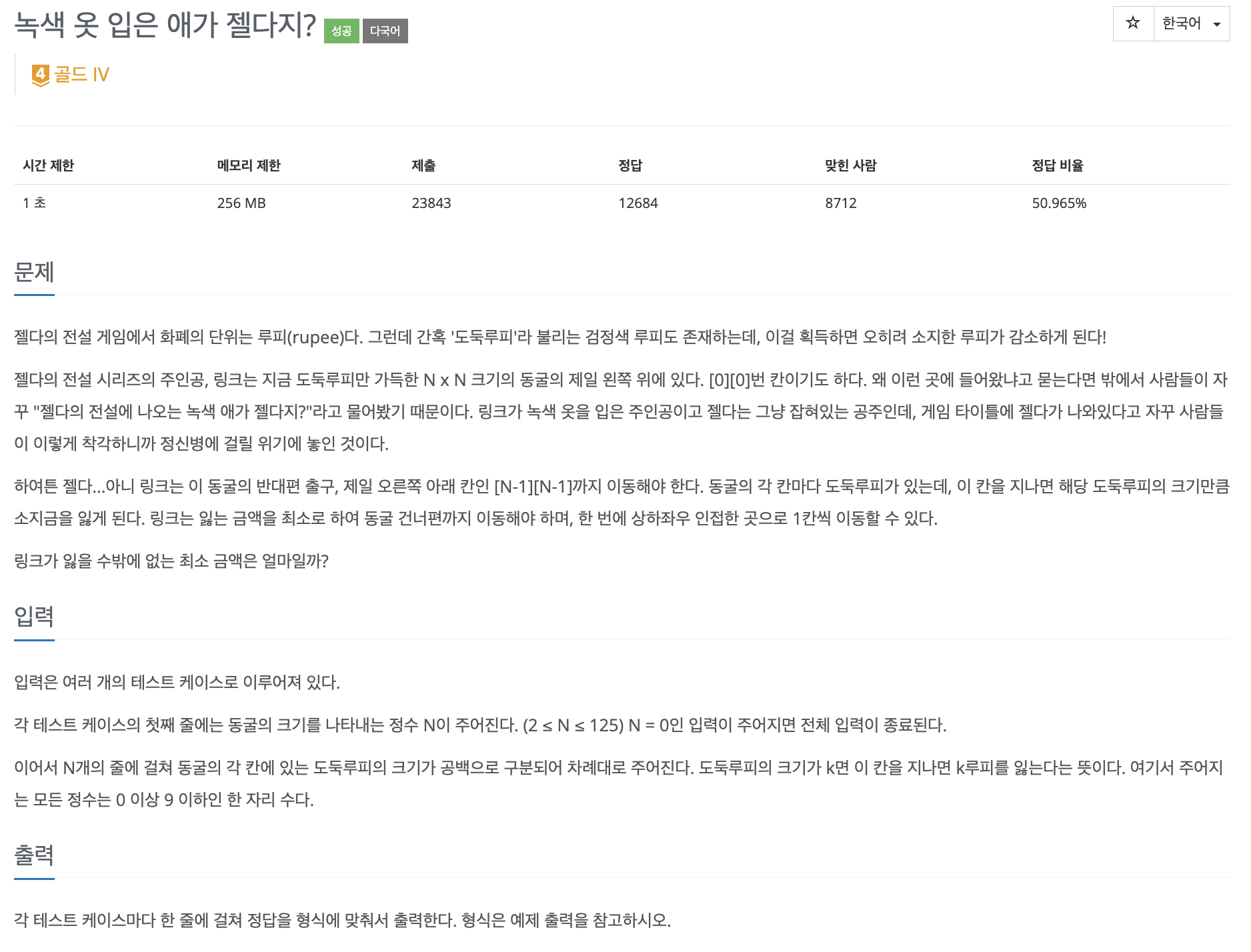
문제 링크

4485: 녹색 옷 입은 애가 젤다지?

구현 방식

• 이 문제의 경우 bfs로 풀면 안된다

  • bfs는 한번 방문한 노드를 재방문하지 않으므로, 가중치가 있는 그래프에서 최소 cost 경로를 찾지 못할 수가 있음

  • 반면, dijkstra는 더 빠른(최소 cost) 경로가 있다면 방문했던 노드를 재방문 하기도 함

• 따라서 dijkstra를 통해 (0, 0)에서 (N-1, N-1)으로 가는 최소 금액을 찾아주었다

코드

#include <iostream>
#include <vector>
#include <queue>
#include <limits.h>
using namespace std;

#define INF INT_MAX
#define MAX 125

int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};

int N, cnt;
int graph[MAX][MAX];
int costs[MAX][MAX];

void dijkstra(){
    priority_queue<pair<int, pair<int, int> > > PQ;
    PQ.push(make_pair(-graph[0][0], make_pair(0, 0)));
    costs[0][0] = 0;

    while (!PQ.empty()){
        int cost = -PQ.top().first;
        int x = PQ.top().second.first;
        int y = PQ.top().second.second;
        PQ.pop();

        if (x == N-1 && y == N-1){
            cout << "Problem " << cnt << ": " << cost << '\n';
            break;
        }

        for(int i=0; i<4; i++){
            int nx = x + dx[i];
            int ny = y + dy[i];

            if (0 <= nx && nx < N && 0 <= ny && ny < N){
                int ncost = cost + graph[nx][ny];
                if (costs[nx][ny] > ncost){
                    costs[nx][ny] = ncost;
                    PQ.push(make_pair(-costs[nx][ny], make_pair(nx, ny)));
                }
            }
        }
    }
}

int main() {
    cnt = 0;
    while(true){
        cin >> N;
        if (N == 0){
            break;
        }

        cnt++;
        for (int i=0; i<N; i++){
            for (int j=0; j<N; j++){
                costs[i][j] = INF;
                cin >> graph[i][j];
            }
        }

        dijkstra();
    }

    return 0;
}

import sys
import heapq

dx = (0, 0, -1, 1)
dy = (-1, 1, 0, 0)

def dijkstra():
    heap = []; heapq.heappush(heap, (graph[0][0], 0, 0))
    costs[0][0] = 0

    while heap:
        cost, x, y = heapq.heappop(heap)

        if (x, y) == (N-1, N-1):
            print("Problem " + str(cnt) + ": " + str(cost)); break

        for i in range(4):
            nx, ny = x + dx[i], y + dy[i]
            if 0 <= nx < N and 0 <= ny < N:
                ncost = cost + graph[nx][ny]
                if costs[nx][ny] > ncost:
                    costs[nx][ny] = ncost
                    heapq.heappush(heap, (ncost, nx, ny))


cnt = 0
while True:
    cnt += 1; N = int(sys.stdin.readline()[:-1])
    if N == 0: break

    graph = [list(map(int, sys.stdin.readline()[:-1].split())) for n in range(N)]
    costs = [[int(10e9)]*N for n in range(N)]

    dijkstra()