LIT(Learn I Today) 내가 오늘 배운 것들에 대한 정리
연결 리스트(Linked List)
연결 리스트(Linked List)란 선형 배열과 비슷하지만 차이가 있다.
선형 배열이 "번호가 붙여진 칸에 원소들을 채워넣는" 방식이라고 한다면, 연결 리스트는 "각 원소들을 줄줄이 엮어서" 관리하는 방식
연결 리스트 기본 구조
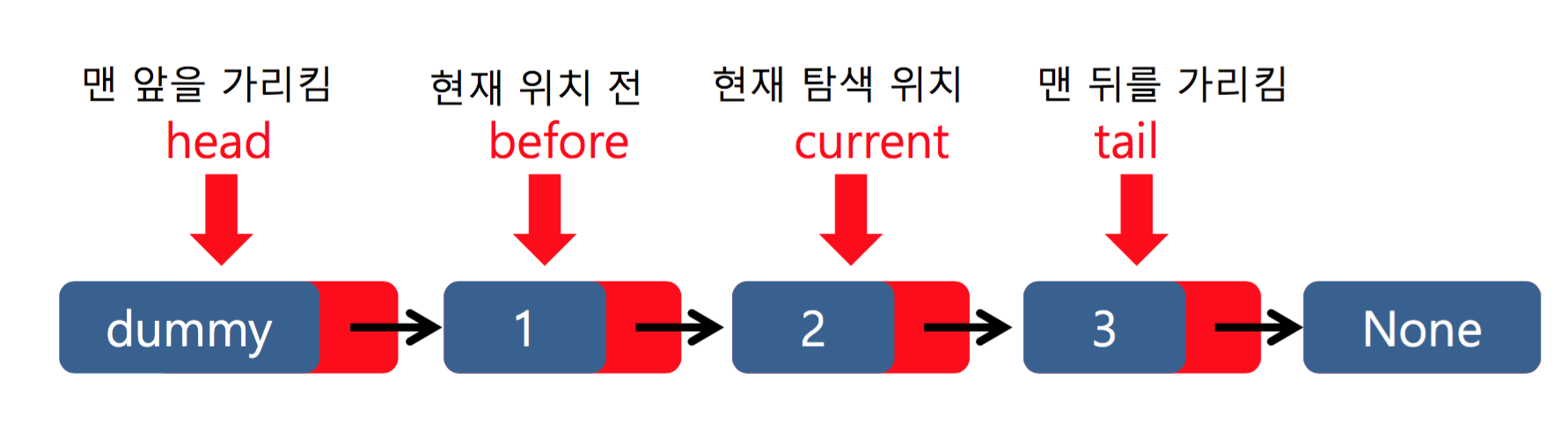
선형 배열에 비해서 연결 리스트가 가지는 장점
- 원소들이 링크라고 부르는 고리로 연결되어 있으므로 가운데에서 끊어 하나를 삭제하거나 삽입하는것이 선형 배열의 경우보다 빠르게 처리가 가능하다.
선형 배열에 비해서 연결 리스트가 가지는 단점
- 선형 배열에 비해서 데이터 구조 표현에 소요되는 저장 공간 (메모리) 소요가 크다.
- 링크 또한 메모리에 저장되어 있어야 하므로, 연결 리스트를 표현하기 위해서는 동일한 데이터 원소들을 담기 위하여 사용하는 메모리 요구량이 더 크다.
- "k 번째의 원소" 를 찾아가는 데에는 선형 배열의 경우보다 시간이 오래 걸린다.
원소의 삽입 (insertion)
def insertAt(self, pos, newNode):
if pos < 1 or pos > self.nodeCount + 1:
return False
if pos == 1:
newNode.next = self.head
self.head = newNode
else:
if pos == self.nodeCount + 1:
prev = self.tail
else:
prev = self.getAt(pos - 1)
newNode.next = prev.next
prev.next = newNode
if pos == self.nodeCount + 1:
self.tail = newNode
self.nodeCount += 1
return Truepos가 가리키는 위치에 newNode를 삽입 True/False 리턴(pos 값의 범위: 1 <= pos <= nowCount +1)
- 연결 리스트 삽입 복잡도
- 맨 앞에 삽입하는 경우: O(1)
- 중간에 삽입하는 경우: O(n)
- 맨 끝에 삽입하는 경우: O(1)
원소의 삭제 (deletion)
- pos가 가리키는 위치의 node를 삭제하고
- 그 node의 데이터를 리턴(r = L.popAt(pos))
(이때, pos의 범위: 1 <= pos <= nodeCount)
- 연결 리스트 삭제 복잡도
- 맨 앞에 삭제하는 경우: O(1)
- 중간에 삭제하는 경우: O(n)
- 맨 끝에 삭제하는 경우: O(n)
두 리스트 합치기 (concatenation)
def concat(self, L):
self.tail.next = L.head.next
if L.tail:
self.tail = L.tail
self.nodeCount += L.nodeCount- 연결 리스트 self의 뒤에 또 다른 연결 리스트인 L을 이어 붙인다
- L1 = self의 tail의 next가 L2 = L의 head를 가리키는 구조
양방향 연결 리스트 (Doubly Linked Lists)
양방향 연결 리스트 (Doubly Linked Lists)란, 연결 리스트에서는 먼저 오는 데이터 원소를 담은 노드로부터 그 뒤에 오는 데이터 원소를 담은 노드를 향하는 방향으로만 연결되어 있었다. 양방향 연결 리스트에서는 노드들이 앞/뒤로 연결되어 있습니다.
양방향 연결 리스트가 가지는 장점
- 데이터 원소들을 차례로 방문할 때, 앞에서부터 뒤로도 할 수 있지만 뒤에서부터 앞으로도 할 수 있다는 점.
양방향 연결 리스트가 가지는 단점
- 링크를 나타내기 위한 메모리 사용량이 늘어나다.
- 원소를 삽입/삭제하는 연산에 있어서 앞/뒤의 링크를 모두 조정해 주어야 하기 때문에 프로그래머가 조금 더 귀찮아진다.
스택 (Stacks)
스택 (Stacks)이란, 추가된 데이터 원소들을 끄집어내면 마지막에 넣었던 것부터 넣은 순서의 역순으로 꺼내지는 자료 구조.
후입선출 (LIFO: last-in first-out) 자료 구조
스택 연산
-
size(): 현재 스택에 들어 있는 데이터 원소의 수를 구함 -
isEmpty(): 현재 스택이 비어 있는지를 판단 (size() == 0?) -
push(x): 데이터 원소 x 를 스택에 추가 -
pop(): 스택에 가장 나중에 저장된 데이터 원소를 제거 (또한, 반환) -
peek(): 스택에 가장 나중에 저장된 데이터 원소를 참조 (반환), 그러나 제거하지는 않음
스택의 응용 - 수식의 후위 표기법
사용하는 이유: 후위 표기법을 이용하면, 괄호를 쓰지 않고도 연산의 우선순위를 수식에 표현할 수 있다.
-
예를 들어
(A + B) * (C + D)를 후위 표기법으로 변환하여 쓰면
->A B + C D + * -
연산과정
숫자를 저장하는 스택: number_stack[ ]
A B + C D + *
1. A,B,C,D 같은 숫자를 만나면 스택에 숫자를 저장한다.
2.+-/*와 같은 연산기호를 만나면 숫자 스택에서 두개 씩 꺼낸다. 이때 스택의 성질에 따라 뒤에서 두개의 숫자가 나온다.
3. 두 숫자를 연산 기호에 맞게 연산한뒤 결과 값을 다시 스택에 저장한다.
