99클럽 코테 스터디 17일차 TIL (Binary Tree Inorder Traversal) - LeetCode

말하는 감자·2024년 8월 7일

99클럽 3기

목록 보기

15/42

이제 본격적으로 내가 잘 모르는 내용이 나오기 시작했다..

나름 집중해서 잘 풀어보았다.

1. 오늘의 학습 키워드

트리
순회
중위순회

2. 문제: 94. Binary Tree Inorder Traversal

단계: Easy
주제: Stack, Tree, Depth-First Search, Binary Tree
출처: https://leetcode.com/problems/binary-tree-inorder-traversal/

문제 설명

Given the root of a binary tree, return the inorder traversal of its nodes' values.

Example 1:

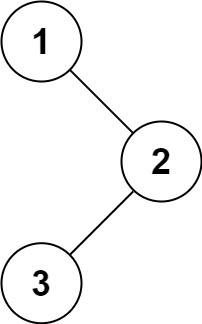
Input: root = [1,null,2,3]
Output: [1,3,2]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Constraints:

The number of nodes in the tree is in the range [0, 100].
100 <= Node.val <= 100

3. 나의 풀이

접근 방법

이 문제는 이진 트리의 root노드가 주어졌을 때, 중위순회 과정의 노드를 리스트에 담아 리턴해라는 문제이다. 그렇다면 순회가 무엇이고, 순회 중 준위 순회가 무엇인지 알아야 한다.

나의 얕은 지식으로는 이 순회의 종류를 결정하는 기준은 root노드이다.

root 노드를 먼저 순회하면 전위, 가운데면 중위, 마지막이면 후위이다. 이 문제는 inorder traversal (중위 순회)이므로, 왼쪽 노드 → root 노드 → 오른쪽 노드 순으로 순회하도록 노드들을 리턴하면 된다.

왼쪽 노드 → root 노드 → 오른쪽 노드 순으로 순회를 반복적! 으로 진행하면 된다.

여기서 반복적이란 단어를 강조했는데, 반복을 할 수 있는 방법은 재귀 함수 사용이 있다.

즉, 왼쪽 노드 → root 노드 → 오른쪽 노드를 재귀적으로 순회하도록 함수를 호출하면 된다!!

코드를 살펴보자.

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution(object):
    def inorderTraversal(self, root):
        # Inorder traversal : 중위 순회로, 왼 -> root -> 오
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        result = []
        def inorder(root):
            if root:
                inorder(root.left) # 루트 노드의 왼쪽 노드
                result.append(root.val) # 루트 노드
                inorder(root.right) # 루트 노드의 오른쪽 노드
        
        inorder(root)
        return result

일단 이렇게 풀어보니 성공은 했다! 하지만 트리 순회를 정리 해보자!

4. 트리 순회

트리의 모든 노드들을 방문하는 과정을 트리 순회 (Tree Traversal)라고 한다.

선형 자료 구조 (연결 리스트, 스택, 큐 등)는 순차적으로 요소에 접근하지만 트리 자료 구조는 다른 방식을 사용해야 한다.

일반적으로 트리 순회에는 다음과 같은 방법들이 있다.

전위 순회 (Preorder)
중위 순회 (Inorder)
후위 순회 (Postorder)

위 세가지 순회 방법들은 재귀로 쉽게 구현되며 DFS (Depth-First Search; 깊이 우선 탐색)의 한 형태이다.

전위 순회 (Preorder Traversal)

트리를 복사하거나, 전위 표기법을 구하는 데 주로 사용된다.

트리를 복사할 때 전위 순회를 사용하는 이유는 트리를 생성할 때 자식 노드보다 부모 노드가 먼저 생성되어야 하기 때문이다.

전위 순회는 다음과 같은 방법으로 진행한다.

Root 노드를 방문한다
왼쪽 서브 트리를 전위 순회한다.
오른쪽 서브 트리를 전위 순회한다.

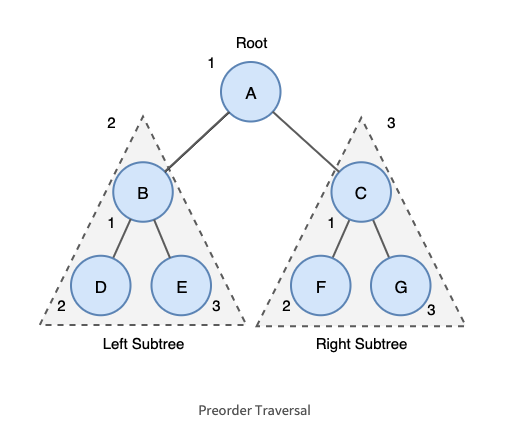
출처:https://yoongrammer.tistory.com/70

위 트리의 전위 순회 결과는 다음과 같다.

A→B→D→E→C→F→G

코드 구현

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def preorder_traversal_recursive(node):
    if node:
        print(node.value, end=' ')
        preorder_traversal_recursive(node.left)
        preorder_traversal_recursive(node.right)

if __name__ == '__main__':
    # 예제 트리 생성
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)

    # 전위 순회 호출
    preorder_traversal_recursive(root) # 1 2 4 5 3

1
/ \
2 3
/ \
4 5

전위 순회 결과: 1→2→4→5→3

중위 순회 (Inorder Traversal)

중위 순회는 이진 탐색 트리에서 오름차순 또는 내림차순으로 값을 가져올 때 사용된다.

내림차순으로 값을 가져오기 위해서는 역순 (오른쪽→root→왼쪽)으로 중위 순회를 하면 된다.

중위 순회는 다음과 같은 방법으로 진행한다.

왼쪽 서브 트리를 중위 순회한다.
Root 노드를 방문한다.
오른쪽 서브 트리를 중위 순회한다.

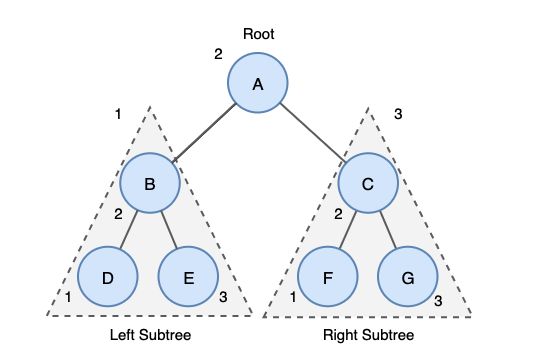
출처:https://yoongrammer.tistory.com/70

위 트리의 중위 순회 결과는 다음과 같다.

D→B→E→A→F→C→G

코드 구현

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def inorder_traversal_recursive(node):
    if node:
        inorder_traversal_recursive(node.left)
        print(node.value, end=' ')
        inorder_traversal_recursive(node.right)

if __name__ == '__main__':
    # 예제 트리 생성
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)

    # 중위 순회 호출
    inorder_traversal_recursive(root) # 4 2 5 1 3

1
/ \
2 3
/ \
4 5

중위 순회 결과: 4→2→5→1→3

후위 순회 (Postorder Traversal)

후위 순회는 트리를 삭제하는 데 주로 사용된다.

이유는 부모 노드를 삭제하기 전에 자식 노드를 삭제하는 순으로 노드를 삭제해야 하기 때문이다.

후위 순회는 다음과 같은 방법으로 진행한다.

왼쪽 서브 트리를 후위 순회한다.
오른쪽 서브 트리를 후위 순회한다.
Root 노드를 방문한다.

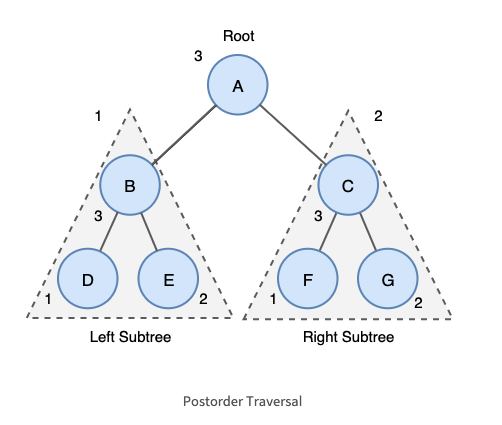
-70ae99fb39cc/ae55b38f-b7ec-43c9-af4e-66e88c36146e/Untitled.png)

출처:https://yoongrammer.tistory.com/70

위 트리의 후위 순회 결과는 다음과 같다.

D→E→B→F→G→C→A

코드 구현

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def postorder_traversal_recursive(node):
    if node:
        postorder_traversal_recursive(node.left)
        postorder_traversal_recursive(node.right)
        print(node.value, end=' ')

if __name__ == '__main__':
    # 예제 트리 생성
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)

    # 후위 순회 호출
    postorder_traversal_recursive(root) # 4 5 2 3 1

1
/ \
2 3
/ \
4 5

후위 순회 결과: 4→5→2→3→1

5. 다른 풀이

이 문제는 중위 순회 문제로 스택을 사용해서도 구현할 수 있다.

class Solution:
    def inorderTraversal(self, root):
        res = []
        stack = []
        curr = root
        while curr or stack: 
            while curr:
                stack.append(curr)
                curr = curr.left
            curr = stack.pop()
            res.append(curr.val)
            curr = curr.right
        return res