
오늘 문제는 99클럽 코테 스터디를 하면서 가장 배울게 많은? 내용의 문제였다고 생각합니다. 문제는 어떻게보면 비교적 간단히 두 노드간의 path가 있는지 없는지를 판단하는 문제이지만 접근 과정에 따라 다양한 방법이 존재합니다. 그럼 살펴 봅시다!
1. 오늘의 학습 키워드
- 그래프
- DFS
- BFS
- Union-Find
2. 문제: 1971. Find if Path Exists in Graph
- 단계: Easy
- 주제: Depth-First Search, Breadth-First Search, Union Find, Graph
- 출처: https://leetcode.com/problems/find-if-path-exists-in-graph/
문제 설명
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
You want to determine if there is a valid path that exists from vertex source to vertex destination.
Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise.
Example 1:
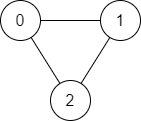
Input: n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2
Example 2:
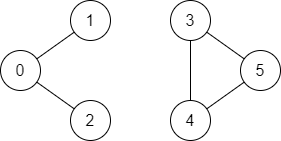
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.
Constraints:
1 <= n <= 2 * 1050 <= edges.length <= 2 * 105edges[i].length == 20 <= ui, vi <= n - 1ui != vi0 <= source, destination <= n - 1- There are no duplicate edges.
- There are no self edges.
3. 나의 풀이
접근 방법
이 문제를 보자마자 떠올랐던 방법은 바로 사이클 유무를 판단하는 union-find 알고리즘이였습니다. 물론 DFS, BFS알고리즘도 떠올렸지만 구현적으로 당장 생각나지 않아 union-Find 알고리즘을 선택했습니다.
아무래도 석사 과정때 처음 연구했던것이 그래프내 사이클관련 연구를 진행했기 때문에 먼저 떠올랐던 것 같습니다.
그렇다면 Union-Find 알고리즘이 무엇인지 알야아 합니다!.
이것은 추후 포스팅을 따로 할 예정이므로 우선 간단하게 개념만 짚고 넘어가보겠습니다.
Union-Find 알고리즘
Disjoint Set을 표현할 때 사용하는 알고리즘으로 트리 구조를 활용하는 알고리즘이다. 간단하게, 노드들 중에 연결된 노드를 찾거나, 노드들을 서로 연결할 때 (합칠 때) 사용한다.
즉, 여러 개의 노드가 존재할 때 두 개의 노드를 선택해서, 현재 이 두 노드가 서로 같은 그래프에 속하는지 판별하는 알고리즘 입니다.
- 초기화
- n 개의 원소가 개별 집합으로 이뤄지도록 초기화

- n 개의 원소가 개별 집합으로 이뤄지도록 초기화
- Union
- 두 개별 집합을 하나의 집합으로 합침, 두 트리를 하나의 트리로 만듬
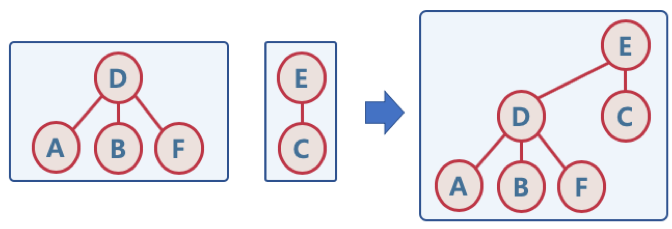
- 두 개별 집합을 하나의 집합으로 합침, 두 트리를 하나의 트리로 만듬
- Find
- 여러 노드가 존재할 때, 두 개의 노드를 선택해서, 현재 두 노드가 서로 같은 그래프에 속하는지 판별하기 위해, 각 그룹의 최상단 원소 (즉, 루트 노드)를 확인
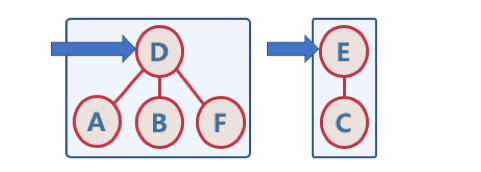
- 여러 노드가 존재할 때, 두 개의 노드를 선택해서, 현재 두 노드가 서로 같은 그래프에 속하는지 판별하기 위해, 각 그룹의 최상단 원소 (즉, 루트 노드)를 확인
근데, 왜 저는 Union-Find 알고리즘을 떠올렸을까요?
이 문제는 source 노드, destination 노드가 주어졌을 때,
이 두 노드가 연결이 되는지를 파악하는 문제입니다.
만약 union-find과정을 거쳐 두 노드가 union이 되지 않는다면 두 노드를 연결하는 valid한 path가 없다는 것을 의미합니다.
즉, 서로 다른 connected component에 있다는 것입니다.
따라서 저는 이 알고리즘을 선택하게 되었습니다.
한 번, 코드 구현을 천천히 살펴보겠습니다.
아래 코드에서는 주어진 무방향 그래프에서 특정 source 정점에서 destination 정점까지 유효한 경로가 존재하는지 확인하는 문제를 Union-Find 알고리즘을 사용했습니다.
코드 설명:
-
Parent 배열 초기화:
parent = list(range(n))- 이 줄에서는 각 정점이 자신을 부모로 가지는
parent배열을 초기화합니다. 이parent배열은 그래프에서 연결된 컴포넌트(즉, 서로 연결된 정점들)를 추적하는 데 사용됩니다. i번 정점의 경우,parent[i]는 그 정점이 속한 집합의 대표(또는 루트) 정점을 나타냅니다.
- 이 줄에서는 각 정점이 자신을 부모로 가지는
-
Find 함수 (경로 압축):
def find(node): if parent[node] != node: parent[node] = find(parent[node]) return parent[node]find함수는 특정 노드가 속한 집합의 루트를 찾는 역할을 합니다. 이 과정에서 경로 압축 (path compression 기법)을 사용하여 트리 구조를 평평하게 만들어, 이후의 검색이 더 빠르게 이루어지도록 합니다.node의 부모가 자신이 아닌 경우, 재귀적으로 부모의 루트를 찾아주며, 이 과정에서node의 부모를 직접 루트로 갱신합니다.
-
집합의 합치기 (Union):
for h, t in edges: parent[find(h)] = find(t)- 이 루프에서는 그래프의 모든 에지를 순회하며, 각 에지
[h, t]에 대해 두 노드h와t를 연결합니다. 이를 위해h의 루트를t의 루트로 설정해 주며, 이렇게 함으로써h와t가 동일한 연결 컴포넌트 (connected component)에 속하게 됩니다.
- 이 루프에서는 그래프의 모든 에지를 순회하며, 각 에지
-
유효한 경로 확인:
return find(source) == find(destination)- 마지막으로, 소스와 목적지 노드가 동일한 연결 컴포넌트 (connected component)에 속하는지를 확인합니다. 이를 위해 두 정점의 루트를 비교하며, 루트가 같으면 두 정점 간에 유효한 경로가 존재하므로
true를 반환하고, 그렇지 않으면false를 반환합니다.
- 마지막으로, 소스와 목적지 노드가 동일한 연결 컴포넌트 (connected component)에 속하는지를 확인합니다. 이를 위해 두 정점의 루트를 비교하며, 루트가 같으면 두 정점 간에 유효한 경로가 존재하므로
예시 설명:
- 예시 1에서 에지는
[[0,1],[1,2],[2,0]]입니다. 이 간선들을 통해 모든 노드(0, 1, 2)는 같은 루트를 가지게 됩니다. 따라서 노드0에서2로 가는 경로가 존재하며, 함수는true를 반환합니다. - 예시 2에서 에지는
[[0,1],[0,2],[3,5],[5,4],[4,3]]입니다. 여기서는 노드 0과 5가 다른 연결 컴포넌트 (connected component)에 속하게 되므로, 함수는false를 반환합니다.
전체 코드를 확인하기전 위에서 계속 나왔던 단어 Connected Component에 대해간략하게 짚고 넘어가겠습니다.
Connected component란?
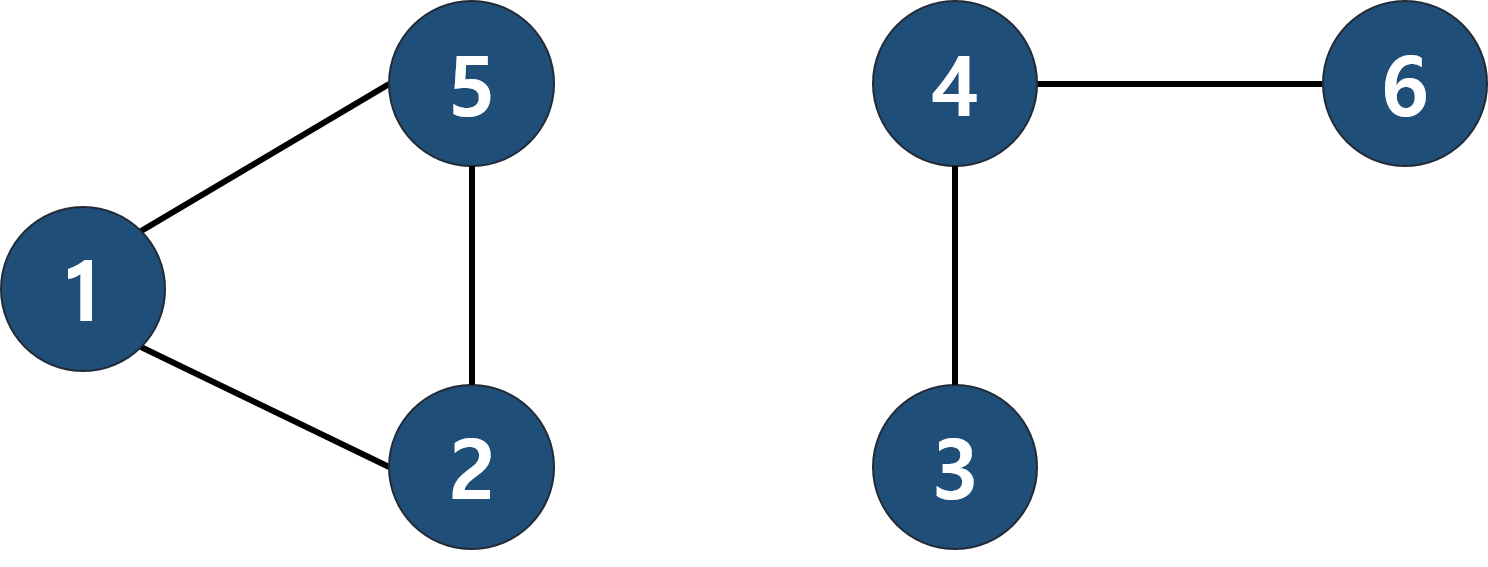
그래프 중에서는 위 그림과 같이 여러 개로 나누어져 있을 수도 있다. 위 그림을 보고 두 개의 그래프라고 볼 수도 있지만, 하나의 그래프에 두 개의 연결 요소를 가진다고 볼 수도 있다. 그 이유는 정점 사이에 겹치는 것이 없기 때문이다. 연결 요소로 본다면, 나누어진 각각의 그래프를 연결 요소라고 한다. 이때 연결 요소가 될 조건은 다음과 같다.
- 연결 요소에 속한 모든 정점을 연결하는 경로가 있어야 한다.
- 또 다른 연결 요소에 속한 정점과 연결하는 경로가 있으면 안된다.
그러므로, 위 그림은 2개의 연결 요소로 이루어져 있다고 볼 수 있다.
전체 코드는 아래와 같습니다.
class Solution(object):
def validPath(self, n, edges, source, destination):
"""
:type n: int
:type edges: List[List[int]]
:type source: int
:type destination: int
:rtype: bool
"""
# N : node
# E : edge
# initialize parent
parent = list(range(n)) # O(N)
# find root (path compression algorithm)
def find(node):
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
for h,t in edges: # O(E * α(N))
parent[find(h)] = find(t)
return find(source) == find(destination) # O(α(N))
# O(N+E)시간 복잡도 분석
이 코드의 시간 복잡도를 분석해보겠습니다.
Union-Find 구조의 시간 복잡도:
Union-Find 알고리즘은 크게 두 가지 연산으로 구성됩니다:
- Find 연산 (find 함수)
- Union 연산 (두 집합을 합치는 연산)
이 두 연산 모두 경로 압축(path compression)과 랭크 기반 유니온(rank-based union)을 사용할 경우, 거의 상수 시간에 가까운 시간 복잡도를 가집니다.
이를 역아커만 함수(Inverse Ackermann function)인 O(α(n))로 표현합니다.
이 함수는 매우 천천히 증가하는 함수로, 현실적인 입력 크기에서는 거의 상수 시간에 가깝습니다.
코드 전체의 시간 복잡도:
-
Parent 배열 초기화:
parent = list(range(n))- 이 부분은
O(n)의 시간 복잡도를 가집니다.n개의 정점을 초기화하는 작업이기 때문입니다.
- 이 부분은
-
Union 연산을 수행하는 루프:
for h, t in edges: parent[find(h)] = find(t)- 이 부분에서는
m개의 간선에 대해find연산을 두 번 수행하고,union연산을 한 번 수행합니다. 각 연산이O(α(n))의 시간 복잡도를 가지므로, 이 루프 전체는O(m * α(n))의 시간 복잡도를 가집니다.
- 이 부분에서는
-
마지막 경로 확인:
return find(source) == find(destination)- 이 부분은 두 번의
find연산을 수행하므로,O(α(n))의 시간 복잡도를 가집니다.
- 이 부분은 두 번의
종합적인 시간 복잡도:
parent배열 초기화:O(n)- 모든 간선에 대한 Union 연산:
O(m * α(n)) - 최종 경로 확인:
O(α(n))
이를 모두 합치면, 최종 시간 복잡도는 O(n + m * α(n))가 됩니다. 여기서 α(n)은 대부분의 실질적인 입력 크기에 대해 거의 상수에 가깝기 때문에, 시간 복잡도는 사실상 O(n + m)로 간주할 수 있습니다.
따라서 이 알고리즘은 매우 효율적이며, 정점 수 n과 간선 수 m에 대해 선형 시간에 가까운 성능을 보여줍니다.
결과
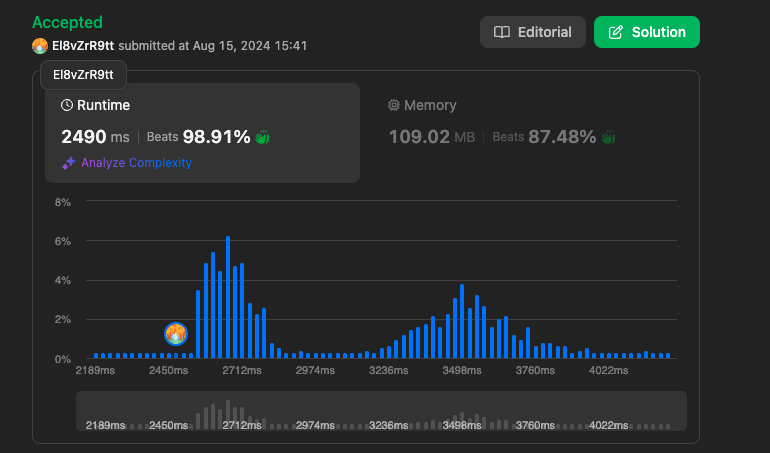
https://leetcode.com/problems/find-if-path-exists-in-graph/submissions/1356234226
확실히 속도가 빠른 것을 확인할 수 있습니다.
4. 다른 풀이
이 문제는 DFS (Depth-First Search)나 BFS ( Breadth-Frist Search)로도 해결할 수 있습니다.
DFS, BFS는 그래프에서 특정 정점에서 다른 정점으로 도달 가능한지 확인할 때 자주 사용되는 탐색 알고리즘입니다.
DFS 풀이
DFS 알고리즘은 재귀적으로 또는 스택 자료구조를 사용해 그래프를 깊이 우선으로 탐색하는 알고리즘입니다.
스택 자료구조를 활용한 풀이 방법
class Solution:
def validPath(self, n, edges, source, destination):
from collections import defaultdict
# 그래프를 인접 리스트 형태로 변환
graph = defaultdict(list)
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
# 방문 여부를 저장하는 배열
visited = [False] * n
# 스택을 사용한 DFS
stack = [source]
while stack:
node = stack.pop()
# 목적지에 도달하면 True 반환
if node == destination:
return True
# 현재 노드를 방문했음을 기록
if not visited[node]:
visited[node] = True
# 인접한 노드들을 스택에 추가
for neighbor in graph[node]:
if not visited[neighbor]:
stack.append(neighbor)
# 목적지에 도달하지 못했을 경우 False 반환
return False
시간복잡도: O(V+E)
결과
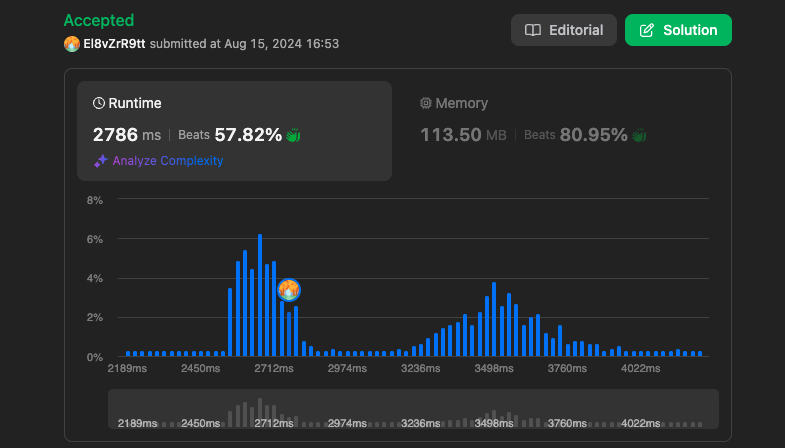
https://leetcode.com/problems/find-if-path-exists-in-graph/submissions/1356305804
재귀적으로 접근한 풀이 방법
class Solution:
def validPath(self, n, edges, source, destination):
from collections import defaultdict
# 그래프를 인접 리스트 형태로 변환
graph = defaultdict(list)
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
# 방문 여부를 저장하는 배열
visited = [False] * n
def dfs(node):
# 현재 노드를 방문했음을 기록
if node == destination:
return True
visited[node] = True
# 인접한 노드들을 방문
for neighbor in graph[node]:
if not visited[neighbor]:
if dfs(neighbor):
return True
return False
# DFS 시작
return dfs(source)
시간복잡도: O(V+E)
결과
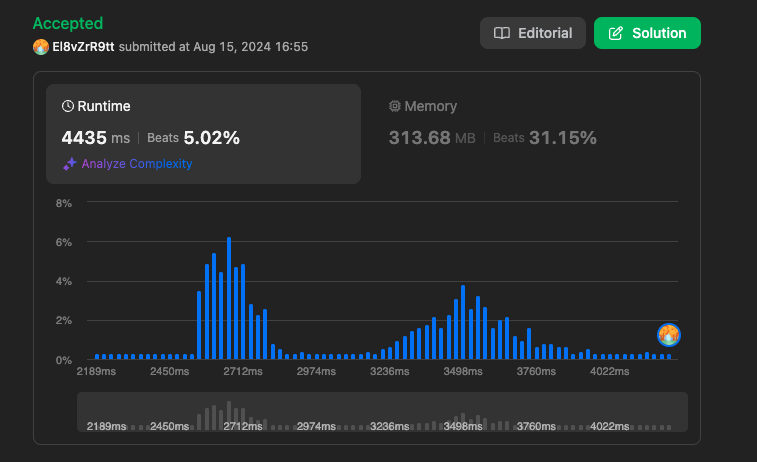
https://leetcode.com/problems/find-if-path-exists-in-graph/submissions/1356307072
BFS 풀이
BFS는 큐를 사용해 그래프를 너비 우선으로 탐색하는 알고리즘입니다.
from collections import deque
class Solution:
def validPath(self, n, edges, source, destination):
from collections import defaultdict
# 그래프를 인접 리스트 형태로 변환
graph = defaultdict(list)
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
# 방문 여부를 저장하는 배열
visited = [False] * n
# 큐를 사용한 BFS
queue = deque([source])
while queue:
node = queue.popleft()
# 목적지에 도달하면 True 반환
if node == destination:
return True
# 현재 노드를 방문했음을 기록
if not visited[node]:
visited[node] = True
# 인접한 노드들을 큐에 추가
for neighbor in graph[node]:
if not visited[neighbor]:
queue.append(neighbor)
# 목적지에 도달하지 못했을 경우 False 반환
return False
시간복잡도: O(V+E)
결과
Union-find, DFS, BFS 모두 O(V+E)의 동일한 시간 복잡도를 가지지만, 속도적으로 Union-find가 가장 빨랐다.
그러나 약간의 차이가 있습니다. 이에 대해 조금 더 깊이 설명하겠습니다.
시간 복잡도 비교
- DFS/BFS:
- 시간 복잡도:
O(V + E)V는 그래프의 정점 수,E는 간선 수입니다.- DFS와 BFS는 그래프의 모든 정점과 간선을 순회하며 탐색합니다. 이 때문에 전체 그래프의 크기에 비례하는 시간 복잡도를 가집니다.
- 시간 복잡도:
- Union-Find:
- 시간 복잡도:
O(V + E * α(V))V는 그래프의 정점 수,E는 간선 수입니다.- 여기서
α(V)는 매우 천천히 증가하는 역아커만 함수로, 현실적으로 거의 상수 시간에 가까운 매우 작은 값입니다. 결과적으로O(V + E * α(V))는 실질적으로O(V + E)에 매우 가까운 시간 복잡도를 갖습니다.
- 시간 복잡도:
중요한 차이점
- DFS/BFS는 탐색을 기반으로 한다:
- DFS와 BFS는 실제로 그래프를 탐색하여 소스 정점에서 목적지 정점까지 경로가 존재하는지 확인합니다. 즉, 그래프 내의 모든 정점과 간선을 탐색하면서 작업을 수행합니다.
- Union-Find는 연결성만 확인한다:
- Union-Find 알고리즘은 정점들이 같은 연결 컴포넌트에 속해 있는지를 확인하는 데 사용됩니다. 이 과정에서 간선들의 집합이 효율적으로 관리되므로, 연결 컴포넌트 여부를 매우 빠르게 확인할 수 있습니다.
현실적인 차이
- 실제 성능 차이: 이론적으로 두 알고리즘 모두
O(V + E)의 시간 복잡도를 가지지만, Union-Find의 경로 압축과 랭크 기반 유니온 덕분에, 실제로는 연결성 확인 문제에서 DFS나 BFS보다 더 빠르게 동작할 수 있습니다. 특히, 반복적인 연결성 확인이 필요한 문제에서는 Union-Find가 훨씬 더 효율적입니다. - α(V)의 영향: 비록 시간 복잡도 표기에서
O(V + E * α(V))로 나타내지만,α(V)가 매우 천천히 증가하는 함수이기 때문에 실질적으로 상수 시간에 가까운 성능을 보여줍니다. 이로 인해 Union-Find는 대규모 그래프에서 더 빠르게 동작할 수 있습니다.
결론
DFS와 BFS는 이론적으로 O(V + E) 시간 복잡도를 가지며, Union-Find도 O(V + E)에 매우 근접한 시간 복잡도를 가집니다. 그러나 실제로는 Union-Find가 특정 유형의 문제(특히, 연결성 확인 문제)에서 DFS/BFS보다 더 빠르게 동작할 수 있습니다. 이는 특히 연결 여부를 확인하는 문제가 주어졌을 때, Union-Find가 더 최적화된 해결책을 제공하기 때문입니다.
총 4가지 방법을 두 가지 테스트 케이스에 대해 실험한 전체 코드는 아래와 같습니다.
복사가 안된다면 아래 링크를 참조하세요!
Python/99클럽/Beginner/25일차/1.py at main · jw9603/Python
from collections import defaultdict
from collections import deque
######################## Union-Find #################################
class Solution(object): # O(N+E)
def validPath(self, n, edges, source, destination):
"""
:type n: int
:type edges: List[List[int]]
:type source: int
:type destination: int
:rtype: bool
"""
# N : node
# E : edge
# initialize parent
parent = list(range(n)) # O(N)
# find root (path compression algorithm)
def find(node):
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
for h,t in edges: # O(E * α(N))
parent[find(h)] = find(t)
return find(source) == find(destination) # O(α(N))
######################## Union-Find #################################
################### DFS - 1 (using Stack) ######################
class Solution_dfs1: # O(N+E)
def validPath(self,n,edges,source,destination):
graph = defaultdict(list)
# 그래프를 인접 리스트 형태로 변환
for u,v in edges:
graph[u].append(v)
graph[v].append(u)
# 이미 방문한 노드들을 저장하는 배열
visited = [False] * n
# stack: 방문이 필요한 노도들을 저장하는 배열
stack = [source]
while stack:
node = stack.pop()
if node == destination:
return True
# 현재 노드를 방문했음을 기록
if not visited[node]:
visited[node] = True
# 인접한 노드들을 스택에 추가
for neighbor in graph[node]:
if not visited[neighbor]:
stack.append(neighbor)
return False
################### DFS - 1 (using Stack) ######################
################### DFS - 2 (using recursive function) ######################
class Solution_dfs2: # O(N+E)
def validPath(self,n,edges,source,destination):
graph = defaultdict(list)
# 그래프를 인접 리스트 형태로 변환
for u,v in edges:
graph[u].append(v)
graph[v].append(u)
# 이미 방문한 노드들을 저장하는 배열
visited = [False] * n
def dfs(node):
if node == destination:
return True
visited[node] = True
for neighbor in graph[node]:
if not visited[neighbor]:
if dfs(neighbor):
return True
return False
return dfs(source)
################### DFS - 2 (using recursive function) ######################
################### BFS (using Queue) ######################
class Solution_bfs: # O(N+E)
def validPath(self,n,edges,source,destination):
graph = defaultdict(list)
# 그래프를 인접 리스트 형태로 변환
for u,v in edges:
graph[u].append(v)
graph[v].append(u)
# 이미 방문한 노드들을 저장하는 리스트
visited = [False] * n
# 방문이 필요한 노드들을 저장하는 큐
queue = deque([source])
while queue:
node = queue.popleft()
if node == destination:
return True
if not visited[node]:
visited[node] = True
for neighbor in graph[node]:
if not visited[neighbor]:
queue.append(neighbor)
return False
################### BFS (using Queue) ######################
# Test case
if __name__ == '__main__':
a = Solution()
b = Solution_dfs1()
c = Solution_dfs2()
d = Solution_bfs()
# Test Case 1
res_uf1 = a.validPath(3,[[0,1],[1,2],[2,0]],0,2)
res_dfs1 = b.validPath(3,[[0,1],[1,2],[2,0]],0,2)
res_dfs11 = c.validPath(3,[[0,1],[1,2],[2,0]],0,2)
res_bfs1 = d.validPath(3,[[0,1],[1,2],[2,0]],0,2)
print('Test case1 Result using union-find algorithm',res_uf1)
print('Test case1 Result using DFS(stack) algorithm',res_dfs1)
print('Test case1 Result using DFS(recursive) algorithm',res_dfs11)
print('Test case1 Result using BFS algorithm',res_bfs1)
# Test Case 2
res_uf2 = a.validPath(6,[[0,1],[0,2],[3,5],[5,4],[4,3]],0,5)
res_dfs2 = b.validPath(6,[[0,1],[0,2],[3,5],[5,4],[4,3]],0,5)
res_dfs21 = c.validPath(6,[[0,1],[0,2],[3,5],[5,4],[4,3]],0,5)
res_bfs2 = d.validPath(6,[[0,1],[0,2],[3,5],[5,4],[4,3]],0,5)
print('Test case1 Result using union-find algorithm',res_uf2)
print('Test case1 Result using DFS(stack) algorithm',res_dfs2)
print('Test case1 Result using DFS(recursive) algorithm',res_dfs21)
print('Test case1 Result using BFS algorithm',res_bfs2)5. 결론
그래도 그래프 연구를 좀 했다고, 알고리즘을 비교적 잘 푼 것 같았다. 연결성을 확인하니까 탐색 알고리즘인 DFS, BFS보단 union-find를 바로 생각했다는점!!
앞으로 더 발전하자!
읽어주셔서 감사합니다.
