99클럽 코테 스터디 10일차 TIL (Kth Largest Element in a Stream) - Leet Code

9일차에 이어 오늘도 LeetCode에서 출제한 문제!!

---

1. 오늘의 학습 키워드

• 정렬

나는 정렬이라 생각했지만, 이 문제는 heap으로 풀 수 있다고 한다..

---

2. 문제: 703. Kth Largest Element in a Stream

• 단계: Easy
• 주제: Tree, Design, Binary Search Tree, Heap, Binary Tree, Data Stream
• 출처: https://leetcode.com/problems/kth-largest-element-in-a-stream/

문제 설명

Design a class to find the kth largest element in a stream. Note that it is the kth largest element in the sorted order, not the kth distinct element.

Implement KthLargest class:

• KthLargest(int k, int[] nums) Initializes the object with the integer k and the stream of integers nums.
• int add(int val) Appends the integer val to the stream and returns the element representing the kth largest element in the stream.

Example 1:

Input
["KthLargest", "add", "add", "add", "add", "add"]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
Output
[null, 4, 5, 5, 8, 8]

Explanation
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3);   // return 4
kthLargest.add(5);   // return 5
kthLargest.add(10);  // return 5
kthLargest.add(9);   // return 8
kthLargest.add(4);   // return 8

Constraints:

• 1 <= k <= 104
• 0 <= nums.length <= 104
• 104 <= nums[i] <= 104
• 104 <= val <= 104
• At most 104 calls will be made to add.
• It is guaranteed that there will be at least k elements in the array when you search for the kth element.

---

3. 나의 풀이

접근 방법

문제의 내용을 정리하면서 접근해보자.

리스트에서 K번째 요소를 찾는 클래스를 만들자! 라는 문제이다.

초기화 메서드에서는 k값과, 어떤 값이 들어있는 리스트 nums가 주어진다.

add 메서드에서는 val이란 정수를 nums 리스트에 넣고, nums 리스트에서 k번째에 해당하는 값을 리턴하는 메서드로 작성하면 된다.

초기화 메서드

nums를 내림차순으로 만들고 k번째전까지의 값만을 nums에 저장한다.

굳이 전체 nums를 가지고 있을 필요가 없기 때문이다. → 메모리 효율적

하지만, 속도는 약간 감소할 것이다.

class KthLargest(object):

    def __init__(self, k, nums):
        """
        :type k: int
        :type nums: List[int]
        """
        self.k = k
        self.nums = sorted(nums,reverse=True)[:k]

add 메서드

val 값을 넣고, 다시 내림차순으로 정렬하고 k번째 값을 return한다.

def add(self, val):
        """
        :type val: int
        :rtype: int
        """
        self.nums.append(val)
        self.nums = sorted(self.nums,reverse=True)[:self.k]
        
        return self.nums[-1]

최종 코드

class KthLargest(object):

    def __init__(self, k, nums):
        """
        :type k: int
        :type nums: List[int]
        """
        self.k = k
        self.nums = sorted(nums,reverse=True)[:k]
        

    def add(self, val):
        """
        :type val: int
        :rtype: int
        """
        self.nums.append(val)
        self.nums = sorted(self.nums,reverse=True)[:self.k]
        
        return self.nums[-1]
        

# Your KthLargest object will be instantiated and called as such:
obj = KthLargest(k=3, nums=[4,5,8,2])
param_1 = obj.add(3)

print(param_1) # 4

---

4. 다른 풀이 (힙)

이 문제는 힙을 사용해서 풀기 좋다고 한다. LeetCode의 Solution을 살펴보자.

코드를 살펴보면 아래와 같다:

import heapq
class KthLargest:
    def __init__(self, k: int, nums: List[int]):
        self.k = k
        self.heap = nums
        heapq.heapify(self.heap)
        
        while len(self.heap) > k:
            heapq.heappop(self.heap)

    def add(self, val: int) -> int:
        heapq.heappush(self.heap, val)
        if len(self.heap) > self.k:
            heapq.heappop(self.heap)
        return self.heap[0]

---

잠깐, heapq에 대해 알아보고 넘어가자!

파이썬 힙 자료구조

파이썬 heapq 모듈은 heapq (priority queue) 알고리즘을 제공한다.

모든 부모 노드는 그의 자식 노드보다 값이 작거나 큰 완전 이진 트리 구조인데, 내부적으로 인덱스 0에서 시작해 k번째 원소가 항상 자식 원소들 (2k+1, 2k+2)보다 작거나 같은 최소 힙의 형태로 정렬된다.

• 완전 이진 트리란: 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며 마지막 레벨의 모든 노드는 가능한 한 가장 왼쪽에 있다.

힙 함수 활용하기

• heapq.heappush(heap,item): item을 heap에 추가
• heapq.heappop(heap): heap에서 가장 작은 원소를 pop & return. 비어 있는 경우 IndexError가 호출됨.
• heapq.heapify(x): 리스트 x를 즉각적으로 heap으로 변환함 (시간복잡도: O(N))

힙 생성 & 원소 추가

heapq 모듈은 리스트를 최소 힙처럼 다룰 수 있도록 하기 때문에, 빈 리스트를 생성한 후 heapq의 함수를 호출할 때마다 리스트를 인자에 넘겨야 한다.

아래 코드는 heap이라는 빈 리스트를 생성하고 50, 10, 20을 각각 추가하는 예시이다.

import heapq

heap = []
heapq.heappush(heap,50)
heapq.heappush(heap,10)
heapq.heappush(heap,20)

print(heap) # [10, 50, 20]

이미 생성해둔 리스트가 있다면 heapify함수를 통해 최소힙 자료형으로 변환할 수 있다.

heap2 = [50 ,10, 20]
heapq.heapify(heap2)

print(heap2)

힙에서 요소 삭제

heappop 함수는 가장 작은 요소를 힙에서 제거함과 동시에 그를 결과값으로 리턴한다.

result = heapq.heappop(heap)

print(result) # 10
print(heap)  # [20,50]

위의 예제를 보면 가장 작은 원소인 10을 가져오고 난 후에도 heap은 유지되는 것을 볼 수 있다.

그렇다면 최대힙은?

최대 힙 만들기

파이썬에서 제공하는 heapq 모듈은 최소힙을 지원하므로 약간의 트릭이 필요하다.

Trick: y= -x, 즉 값의 부호를 변경하는 방법

힙에 요소를 추가할 때 (-item,item)의 튜플 형태로 넣어주면 튜플의 첫 번째 원소를 우선순위로 힙을 구성하게 된다. 이 때 원소값의 부호를 바꿨기 때문에, 최소 힙으로 구현된 heapq 모듈을 최대 힙 구현에 활용하게 되는 것이다.

아래 코드는 리스트 h에 있는 요소들을 max_heap이라는 최대 힙 자료구조로 만드는 코드이다.

import heapq
h = [1,3,4,5,7,9]

max_heap = []

for i in h:
    heapq.heappush(max_heap,(-i,i))

print(max_heap) # [(-9, 9), (-5, 5), (-7, 7), (-1, 1), (-4, 4), (-3, 3)]

heappush 함수를 통해 item을 힙에 push 할 때 (-item, item)의 튜플의 형태로 넣은 것을 확인할 수 있다.

그 결과 heappop을 사용하게 되면 힙에 있는 최댓값이 반환되는 것을 확인할 수 있다. 이때 실제 원소 값은 튜플의 두 번째 자리에 저장되어 있으므로 [1] 인덱싱을 통해 접근하면 된다.

res = heapq.heappop(max_heap)[-1]
print(res) # 9

---

다시 코드를 살펴본다면, 아래와 같다.

import heapq
class KthLargest:
    def __init__(self, k: int, nums: list[int]):
        self.k = k
        self.heap = nums
        heapq.heapify(self.heap)
        
        while len(self.heap) > k:
            heapq.heappop(self.heap)

    def add(self, val: int) -> int:
        heapq.heappush(self.heap, val)
        if len(self.heap) > self.k:
            heapq.heappop(self.heap)
        return self.heap[0]

이 코드는 최소 힙 자료 구조를 사용했고, k번째 큰 값을 찾기 위해 길이가 k가 될때까지 최소값들을 제거하는 형태의 알고리즘이다.

예시를 들어 보면 확실히 이해가 될 것이다.

리스트 [1,2,3,4,5,6]이 있고, k = 3인 상황에서 4를 더한다하자.

생성자 함수에서 리스트 [1, 2, 3, 4, 5, 6]은 [4, 5, 6]이 된다. 그 다음 4를 더하면,

[4, 4, 5, 6]이 되고, 여기서 길이 3일때까지 자르면 [4, 5, 6]이 나오고 최종적으로 4를 리턴한다.

---

5. 결과

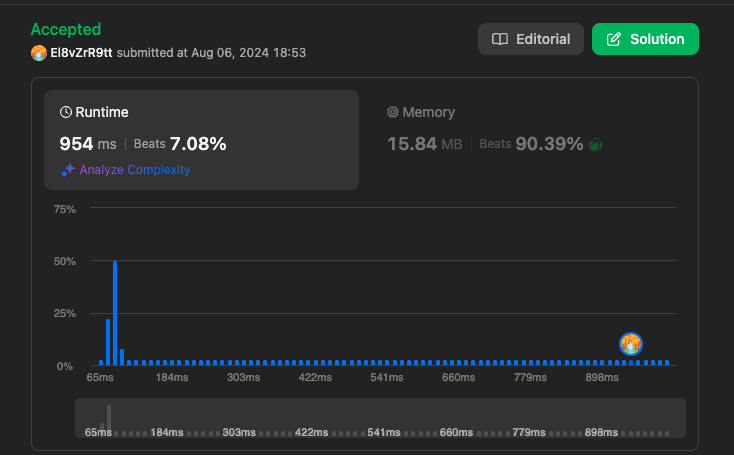
내 풀이

https://leetcode.com/problems/kth-largest-element-in-a-stream/submissions/1346397342

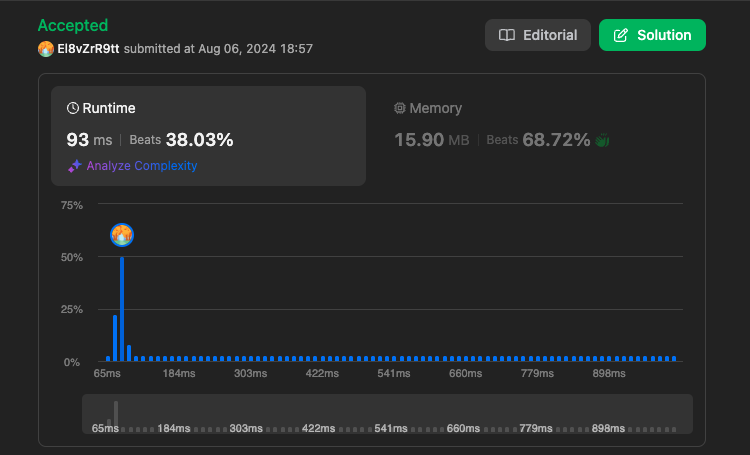
힙 풀이

https://leetcode.com/problems/kth-largest-element-in-a-stream/submissions/1346400846

Time Complexity

Given N as the length of nums and M as the number of calls to add(),

• Time complexity: O(N⋅log(N)+M⋅log(k)) The time complexity is split into two parts. First, the constructor needs to turn nums into a heap of size k. In Python, heapq.heapify() can turn nums into a heap in O(N) time. Then, we need to remove from the heap until there are only k elements in it, which means removing N - k elements. Since k can be, say 1, in terms of big O this is N operations, with each operation costing log(N). Therefore, the constructor costs O(N+N⋅log(N))=O(N⋅log(N)). Next, every call to add() involves adding an element to heap and potentially removing an element from heap. Since our heap is of size k, every call to add() at worst costs O(2∗log(k))=O(log(k)). That means M calls to add() costs O(M⋅log(k)).
  

---

6. 결론

힙에 대한 개념정도만 알았는데, 파이썬에서 힙을 어떻게 사용하는지에 대해 잘 알게된 계기가 되었다.