
요즘 정말 무더운 날씨,,,, 모두 화이팅입니다.
오늘 문제는 그리디 알고리즘 계열의 문제입니다.
1. 오늘의 학습 키워드
- 정렬
- greedy algorithm
2. 문제: 561. Array Partition
- 단계: Easy
- 주제: Array, Greedy, Sorting, Counting Sort
- 출처: https://leetcode.com/problems/array-partition/
문제설명
Given an integer array nums of 2n integers, group these integers into n pairs (a1, b1), (a2, b2), ..., (an, bn) such that the sum of min(ai, bi) for all i is maximized. Return the maximized sum.
Example 1:
Input: nums = [1,4,3,2]
Output: 4
Explanation: All possible pairings (ignoring the ordering of elements) are:
1. (1, 4), (2, 3) -> min(1, 4) + min(2, 3) = 1 + 2 = 3
2. (1, 3), (2, 4) -> min(1, 3) + min(2, 4) = 1 + 2 = 3
3. (1, 2), (3, 4) -> min(1, 2) + min(3, 4) = 1 + 3 = 4
So the maximum possible sum is 4.Example 2:
Input: nums = [6,2,6,5,1,2]
Output: 9
Explanation: The optimal pairing is (2, 1), (2, 5), (6, 6). min(2, 1) + min(2, 5) + min(6, 6) = 1 + 2 + 6 = 9.
Constraints:
1 <= n <= 104nums.length == 2 * n104 <= nums[i] <= 104
3. 나의 풀이
접근 방법
이번 문제는 그리디 알고리즘의 계열이라고 하는데, 제 생각은 억지로 끼워 맞춘 느낌이 강했습니다. 문제를 살펴보면 2n 개의 정수를 포함하는 정수 배열이 주어졌을때, 이 배열을 n 개의 쌍으로 그룹화 합니다. 그룹화 과정은 min(ai, bi) 와 같이 최소값을 구하는 형태로 그룹화를 진행하고, 그룹화된 값들의 합의 최댓값을 구하는것이 이 문제입니다.
즉, 그룹화된 값이 가장 크면, 그릅화된 값들의 합도 최댓값이 되기 때문에 그리디 알고리즘 계열의 문제라고 하는것 같습니다.
이것을 쉽게 적용할려면, 오름차순으로 배열을 정렬하고, 배열의 절반을 나눕니다.
나눠진 절반의 배열들의 합을 구하면 최종적인 값을 구할 수 있습니다.
코드는 아래와 같습니다.
class Solution(object):
def arrayPairSum(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
return sum(sorted(nums)[::2])이것의 테스트 케이스의 결과를 보고자 한다면 다음과 같이 코드를 추가할 수 있습니다.
class Solution(object):
def arrayPairSum(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
return sum(sorted(nums)[::2])
if __name__ == '__main__':
a = Solution()
TestCase1 = a.arrayPairSum([1,4,3,2])
TestCase2 = a.arrayPairSum([6,2,6,5,1,2])
print('TestCase1',TestCase1) # TestCase1 4
print('TestCase2',TestCase2) # TestCase2 9결과
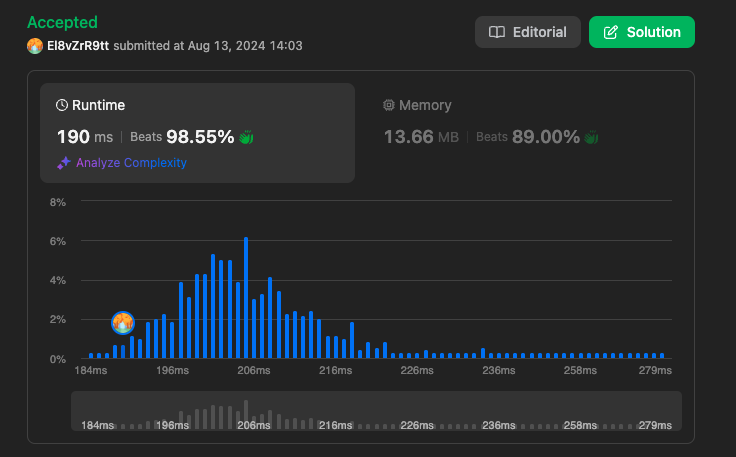
https://leetcode.com/problems/array-partition/submissions/1353898143
4. 결론
이번 문제는 그룹화에서의 결과 (큰 값들을 묶어서 최소값 구하기)가 전체 결과에 영향을 미치는 그리디 알고리즘 계열의 문제였습니다. 약간 그리디 알고리즘이라고 하기엔 비교적 간단했지만, 개념을 잡는데는 적합한 문제라고 여겨집니다.
읽어주셔서 감사합니다.
