99클럽 코테 스터디 33일차 TIL (Number of Good Leaf Nodes Pairs) - LeetCode

말하는 감자·2024년 8월 23일
99클럽99클럽3기DFSGraphTRAVERSALbinary treepython그래프코딩테스트코딩테스트 준비파이썬향해99
2

99클럽 3기

목록 보기
33/42
post-thumbnail

안녕하세요!

오늘은 99클럽 코테 스터디 33일차 입니다. 오늘 졸업식을 해서 늦게 문제를 풀었지만, 이 코테 스터디 동안 가장 가장 어려운 문제가 아니였나 싶습니다.

정말 막막했,,,습니다. 포기할 뻔?

그래도 꾸역꾸역 풀어냈네요.

풀이 시간도 무려 1시간이 넘었네요.. 문제 한 번 살펴볼까요?

1. 오늘의 학습 키워드

  • DFS
  • 그래프
  • traversal

2. 문제: 1530. Number of Good Leaf Nodes Pairs

문제

You are given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.

Return the number of good leaf node pairs in the tree.

Example 1:

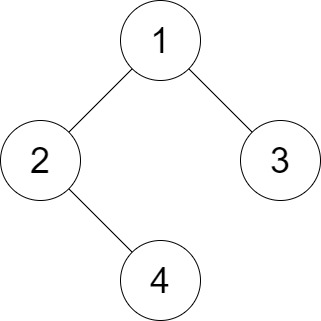
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.

Example 2:

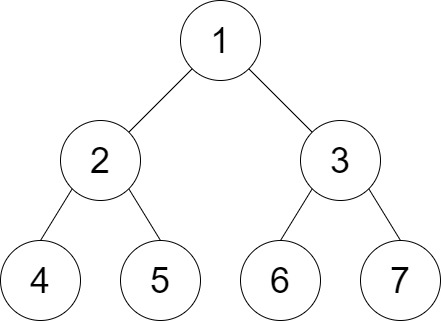
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.

Example 3:

Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].

Constraints:

  • The number of nodes in the tree is in the range [1, 210].
  • 1 <= Node.val <= 100
  • 1 <= distance <= 10

3. 나의 풀이

주어진 문제는 트리의 리프 노드 사이의 경로를 계산하고, 그 경로가 주어진 거리 (distance)를 초과하지 않는 쌍의 개수를 찾는 것입니다. 이를 위해 스택을 이용한 DFS(깊이 우선 탐색) 접근 방식을 사용하였습니다. 아래에서 문제 설명, 접근 방식, 코드 구현 순으로 설명하겠습니다.

문제 설명

주어진 문제는 이진 트리에서 두 개의 리프 노드가 있을 때, 그들 사이의 최단 경로가 주어진 거리 distance 이하인 경우를 "좋은 리프 노드 쌍"이라고 정의합니다. 이 문제에서 해야 할 일은 트리에서 이러한 "좋은 리프 노드 쌍"의 개수를 계산하는 것입니다.

예시

다음과 같은 이진 트리를 고려해봅시다:

   1
  / \\
 2   3
  \\
   4

여기서 리프 노드는 3과 4입니다. 노드 3과 4 사이의 최단 경로는 3 -> 1 -> 2 -> 4로 이루어지며, 이 경로의 길이는 3입니다. 만약 주어진 distance가 3이라면, 이 리프 노드 쌍은 "좋은 쌍"이 됩니다.

접근 방식

저는 이 문제를 해결하기 위해 스택을 이용한 DFS 방법을 사용했습니다.

DFS는 재귀적 방식과 반복적 방식이 있으며, 이 코드에서는 반복적 DFS를 사용하였습니다. 특히, 이 문제에서는 후위 순회가 필요합니다. 즉, 자식 노드를 모두 탐색한 후에 부모 노드에서 결과를 계산해야 합니다.

주요 단계

  1. 스택 초기화: 루트 노드를 스택에 추가하고, 탐색을 시작합니다.
  2. 후위 순회 시뮬레이션: 스택을 이용하여 후위 순회를 수행합니다. 이를 위해 각 노드에 대해 "방문 여부"를 추적합니다.
  3. 리프 노드 처리: 리프 노드일 경우, 그 거리를 초기화합니다.
  4. 거리 정보 업데이트 및 결과 계산: 자식 노드들의 거리 정보를 가져와서 부모 노드의 거리 정보를 계산합니다. 이때 유효한 리프 노드 쌍을 찾습니다.

코드 설명

아래는 위 접근 방식을 구현한 코드입니다.

from collections import deque

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution(object):
    def countPairs(self, root, distance):
        """
        :type root: TreeNode
        :type distance: int
        :rtype: int
        """
        if not root:
            return 0

        result = 0
        stack = deque([(root, False)])
        node_to_distances = {}

        while stack:
            node, visited = stack.pop()
            if not node:
                continue
            
            if visited:  # 노드를 다시 방문했을 때 (후위 순회)
                if not node.left and not node.right:  # 리프 노드인 경우
                    node_to_distances[node] = [1]  # 리프 노드는 자기 자신과의 거리가 1
                else: # 리프 노드가 아닌 경우
                    distances = []
                    if node.left:
                        left_distances = node_to_distances[node.left]
                    else:
                        left_distances = []
                    if node.right:
                        right_distances = node_to_distances[node.right]
                    else:
                        right_distances = []

                    # 유효한 리프 노드 쌍의 개수를 세기
                    for l in left_distances:
                        for r in right_distances:
                            if l + r <= distance:
                                result += 1
                    
                    # 현재 노드의 거리 정보 업데이트
                    for d in left_distances + right_distances:
                        if d + 1 <= distance:
                            distances.append(d + 1)
                    node_to_distances[node] = distances

            else:
                stack.append((node, True))  # 노드를 다시 방문할 때를 표시
                if node.right:
                    stack.append((node.right, False))
                if node.left:
                    stack.append((node.left, False))
        
        return result

참.. 딱 보면 막막하죠? 한 줄씩 설명을 진행해보겠습니다.

from collections import deque
  • collections 모듈의 deque를 임포트: deque는 양쪽 끝에서 빠르게 삽입과 삭제가 가능한 큐입니다. 이 코드는 스택으로 사용됩니다.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
  • 트리 노드 클래스 정의: TreeNode는 이진 트리의 각 노드를 표현합니다. val은 노드의 값을 저장하고, left와 right는 각각 왼쪽 자식과 오른쪽 자식을 가리킵니다.
class Solution(object):
    def countPairs(self, root, distance):
        """
        :type root: TreeNode
        :type distance: int
        :rtype: int
        """
  • 솔루션 클래스 정의 및 함수 선언: Solution 클래스의 countPairs 메서드는 이 문제를 해결하기 위한 메인 함수입니다. 입력으로 이진 트리의 루트 root와 거리 distance를 받습니다.
        if not root:
            return 0
  • 방어 코드: 루트 노드가 None인 경우, 트리가 없다는 의미이므로 "좋은 리프 노드 쌍"이 존재할 수 없습니다. 따라서 0을 반환합니다.
        result = 0
        stack = deque([(root, False)])
        node_to_distances = {}
  • 초기 변수 설정:
    • result: "좋은 리프 노드 쌍"의 개수를 저장할 변수입니다.
    • stack: DFS를 수행할 스택입니다. 여기에는 (노드, 방문 여부) 튜플이 들어갑니다. 루트 노드를 스택에 초기화하면서 False로 방문 여부를 설정합니다.
    • node_to_distances: 각 노드에서 리프 노드까지의 거리 리스트를 저장하는 딕셔너리입니다.

개인적으로 node_to_distances 변수가 이 코드의 완성이라고 생각합니다. 한 번 어떻게 생겼고, 어떤 형태로 이루어지는지 알아볼까요?

node_to_distances 변수는 이 코드에서 매우 중요한 역할을 합니다. 이 변수는 각 노드에서 해당 노드의 자식 리프 노드까지의 거리들을 저장하는 딕셔너리입니다. 각 키는 노드 자체(TreeNode 객체)이고, 값은 그 노드로부터 리프 노드들까지의 거리들을 담고 있는 리스트입니다.

예시를 통해 설명

예를 들어, 아래와 같은 이진 트리가 있다고 가정해보겠습니다.

       1
      / \\
     2   3
        / \\
       4   5

이 트리의 리프 노드는 2, 4, 5입니다.

  1. 리프 노드의 경우:
    • 리프 노드는 자식 노드가 없으므로, 그 자체가 경로의 끝입니다. 따라서 리프 노드에서의 거리는 1로 정의합니다.
    • 예를 들어, 노드 2, 4, 5는 모두 리프 노드이므로, node_to_distances[2], node_to_distances[4], node_to_distances[5]는 각각 [1]이 됩니다.
  2. 비 리프 노드의 경우:
    • 비 리프 노드는 자식 노드의 거리 리스트를 사용하여 자신의 거리 리스트를 구성합니다.
    • 예를 들어, 노드 3은 자식 노드 4와 5가 있습니다. 이 자식 노드들은 각각 [1]이라는 거리 리스트를 가지므로, 노드 3의 거리 리스트는 [2, 2]가 됩니다 (1에 자신까지의 거리인 1을 더해 [2, 2]가 됨).
  3. 루트 노드:
    • 루트 노드 1은 자식 노드 2와 3이 있습니다. 자식 노드 2는 [1], 3은 [2, 2]를 가지고 있으므로, 루트 노드 1의 거리 리스트는 [2, 3, 3]가 됩니다.

node_to_distances는 각 노드에서 리프 노드까지의 거리를 관리하는 딕셔너리로서, 그 노드의 리프 자식들로부터 거리를 받아와 이를 업데이트합니다. 이 딕셔너리는 부모 노드에서 자식 노드까지의 거리를 계산하고, 좋은 리프 노드 쌍을 찾는 데 사용됩니다.

이 변수를 활용해, 후위 순회 과정에서 각 노드가 리프 노드로부터 얼마나 떨어져 있는지를 계산할 수 있으며, 이를 바탕으로 유효한 리프 노드 쌍을 판단할 수 있습니다.

        while stack:
  • DFS 반복문 시작: 스택이 빌 때까지 반복문을 실행합니다.
            node, visited = stack.pop()
  • 스택에서 요소를 꺼냄: 스택의 가장 위에 있는 노드와 그 노드의 방문 여부를 꺼냅니다.
            if not node:
                continue
  • 빈 노드 처리: 노드가 None이면, 이 노드를 건너뜁니다.
            if visited:  # 노드를 다시 방문했을 때 (후위 순회)
  • 후위 순회 단계: 노드가 한 번 방문된 후 다시 스택에 들어온 경우입니다. 이 시점에서는 해당 노드의 자식 노드들이 모두 처리된 상태입니다.
                if not node.left and not node.right:  # 리프 노드인 경우
                    node_to_distances[node] = [1]
  • 리프 노드 처리: 만약 이 노드가 리프 노드라면, 자기 자신과의 거리가 1이므로 [1]을 node_to_distances에 기록합니다.

여기서 잠깐! 저는 왜 node_to_distances 에서 노드가 리프노드일때 거리를 1이라 했을까요?

리프 노드란?

먼저, 리프 노드(Leaf Node)가 무엇인지 짚고 넘어가겠습니다.

  • 리프 노드는 이진 트리에서 자식 노드가 없는 노드를 말합니다. 즉, 트리의 끝에 위치한 노드입니다.
  • 예를 들어, 트리 구조에서 더 이상 아래로 내려갈 수 없는 노드가 리프 노드입니다.

경로와 거리의 개념

트리에서 "경로"란, 한 노드에서 다른 노드로 가는 길을 의미합니다. 이 길에는 여러 노드와 그 노드들 사이의 연결(엣지)이 포함됩니다. "거리"는 이 경로를 따라 이동할 때 거쳐야 하는 연결(엣지)의 수를 의미합니다.

리프 노드에서의 거리

이제 문제에서 요구하는 "리프 노드 간의 거리"에 대해 생각해봅시다.

  • 리프 노드는 더 이상 자식 노드가 없기 때문에, 리프 노드 자체는 어떤 경로의 끝이 됩니다.
  • 리프 노드에서 자기 자신까지의 경로는 아무 연결(엣지)도 없기 때문에, 거리는 0이 되어야 할 것 같다고 생각할 수 있습니다.

하지만, 여기서 "거리"를 정의할 때는 그 리프 노드와 그것을 연결하는 부모 노드 간의 "연결"을 포함하여 계산합니다.

  • 코드에서는 리프 노드가 자기 자신과의 거리를 1로 정의하는 것은, 해당 리프 노드가 부모 노드와 연결되어 있다는 사실을 반영한 것입니다.

예를 들어:

  • 리프 노드 A가 있다고 가정할 때, A가 다른 리프 노드와 연결되어 있지 않다면, "자기 자신과의 거리"는 1로 정의됩니다. 이는 사실상 부모 노드와 연결된 "거리를 1로 생각"하는 것입니다.

간단하게 정리하면:

  • 리프 노드는 더 이상 아래로 내려갈 자식이 없는 트리의 끝 노드입니다.
  • 코드에서 리프 노드의 거리 [1]은 해당 리프 노드가 자기 자신과의 거리를 의미하기보다는, 그 리프 노드가 부모 노드와 연결되어 있다는 의미로 "거리를 1"로 설정한 것입니다.

이렇게 정의하면, 후에 이 리프 노드를 포함한 경로를 계산할 때 부모 노드와의 연결을 쉽게 다룰 수 있게 됩니다.

                else:
                    distances = []
  • 비 리프 노드 처리: 자식 노드들이 있는 경우에, 이 노드의 거리 리스트를 저장할 distances 리스트를 초기화합니다.
                    if node.left:
                        left_distances = node_to_distances[node.left]
                    else:
                        left_distances = []
  • 왼쪽 자식 노드의 거리 정보 가져오기: 왼쪽 자식 노드가 있는 경우, 해당 자식 노드의 거리를 left_distances에 저장합니다. 없다면 빈 리스트를 할당합니다.
                    if node.right:
                        right_distances = node_to_distances[node.right]
                    else:
                        right_distances = []
  • 오른쪽 자식 노드의 거리 정보 가져오기: 오른쪽 자식 노드가 있는 경우, 해당 자식 노드의 거리를 right_distances에 저장합니다. 없다면 빈 리스트를 할당합니다.
                    for l in left_distances:
                        for r in right_distances:
                            if l + r <= distance:
                                result += 1
  • 유효한 리프 노드 쌍 계산:
    • 두 자식 노드로부터 각각 가져온 거리 리스트 left_distances와 right_distances의 모든 쌍을 비교합니다.
    • 두 리프 노드 사이의 경로 길이 l + r이 주어진 distance 이하인 경우, 이 쌍은 "좋은 리프 노드 쌍"이므로 result를 증가시킵니다.
                    for d in left_distances + right_distances:
                        if d + 1 <= distance:
                            distances.append(d + 1)
  • 현재 노드의 거리 리스트 업데이트:
    • 왼쪽 및 오른쪽 자식으로부터 가져온 거리 리스트에서 각각의 값에 1을 더합니다. 이는 현재 노드까지의 경로를 반영하기 위함입니다.
      • 일전에 말씀드린 리프노드 자체의 거리를 1로 했기 때문에, 1을 더하는것입니다.
    • 더한 값이 distance 이하인 경우만 distances 리스트에 추가합니다.
                    node_to_distances[node] = distances
  • 거리 리스트 저장: 현재 노드의 거리 리스트를 node_to_distances에 저장합니다.
            else:
                stack.append((node, True))
  • 다시 방문할 노드 스택에 추가: 처음 방문한 노드라면, 방문 표시를 True로 설정한 후 다시 스택에 추가합니다.
                if node.right:
                    stack.append((node.right, False))
                if node.left:
                    stack.append((node.left, False))
  • 자식 노드 추가: 현재 노드의 오른쪽 자식과 왼쪽 자식을 스택에 추가합니다. 자식 노드들은 방문하지 않은 상태로 추가됩니다.
        return result
  • 결과 반환: 최종적으로 "좋은 리프 노드 쌍"의 개수를 반환합니다.

이 코드는 반복적 DFS를 사용하여 이진 트리에서 두 리프 노드 간의 최단 경로가 주어진 거리 이하인지 확인하고, 그 개수를 세는 방법을 구현합니다. 이 과정에서 스택을 사용하여 후위 순회를 시뮬레이션하고, 각 노드에서 리프 노드까지의 거리를 계산해 나갑니다. 이 방법을 통해 트리의 각 노드에서 유효한 리프 노드 쌍을 효과적으로 계산할 수 있습니다.

4. 다른 풀이

이 문제 푸는데 1시간 30분 걸렸습니다. 정말 어려웠죠,,

하지만 DFS 스택으로 풀었다는 것은 재귀로도 풀 수 있겠죠?

재귀는 오히려 코드 길이가 짧아집니다. 아래 코드를 확인해보겠습니다.

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self,val=0,left=None,right=None):
        self.val =val
        self.left = left
        self.right = right
class Solution(object):
    def countPairs(self, root, distance):
        """
        :type root: TreeNode
        :type distance: int
        :rtype: int
        """
        self.result = 0
        
        def dfs(node):
            if not node:
                return []
            
            if not node.left and not node.right:
                return [1] 

            left_distances = dfs(node.left)
            right_distances = dfs(node.right)
            
            # Count all valid pairs
            for l in left_distances:
                for r in right_distances:
                    if l + r <= distance:
                        self.result += 1
            
            # Return distances to this node's parent
            return [d + 1 for d in left_distances + right_distances if d + 1 <= distance]
        
        dfs(root)
        return self.result

코드의 흐름은 스택을 활용한 방법과 동일합니다!

5. 결과

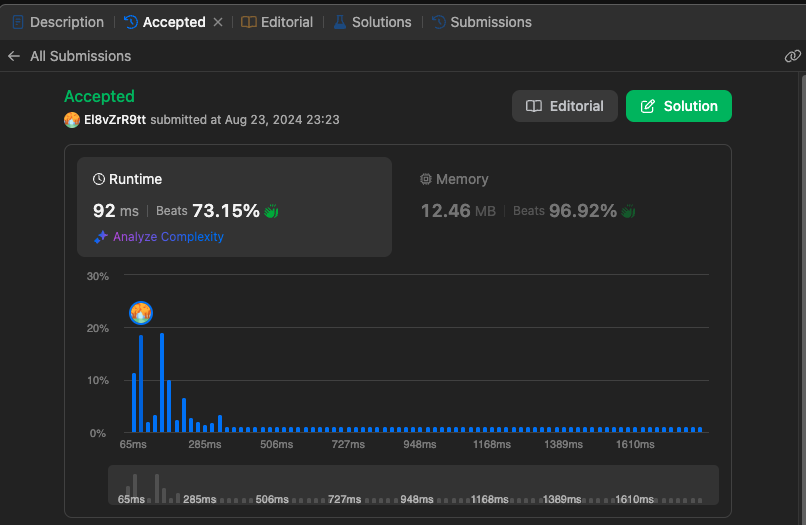
Stack

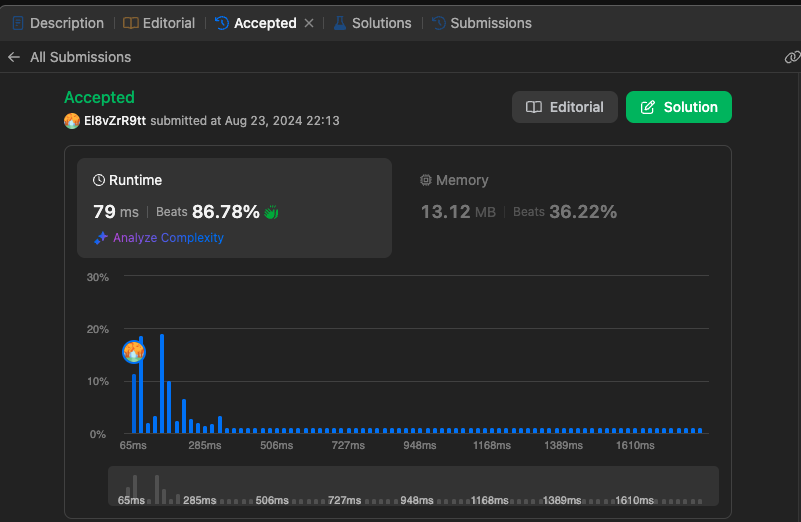
https://leetcode.com/problems/number-of-good-leaf-nodes-pairs/submissions/1365767049?envType=daily-question&envId=2024-07-18

재귀

https://leetcode.com/problems/number-of-good-leaf-nodes-pairs/submissions/1365706863

재귀가 메모리적으로는 덜 효율적이지만 속도적으로는 더 빠른것을 확인할 수 있습니다.

전체 코드는 제 깃허브에서 확인하실수도 있습니다.

6. 결론

오늘 문제는 정말 어려웠습니다. 하지만 그 이유는 제가 코린이 때문이겠죠?

아직 넘어야 할 산이 너무 높네요.. 하지만 끊임없이 도전하겠습니다.

읽어주셔서 감사합니다. 질문은 언제나 환영입니다.

profile
말하는 감자
할 수 있다
이전 포스트

99클럽 코테 스터디 32일차 TIL (Bad Grass) - 백준

다음 포스트

99클럽 코테 스터디 34일차 TIL (양 한마리... 양 두마리...) - 백준

0개의 댓글