
일요일에도 99클럽은 돌아간다,,
오늘은 99클럽 코테 스터디 35일차입니다. 오늘 문제 역시 DFS/BFS 유형의 문제입니다.
1. 오늘의 학습 키워드
- 그래프
- 그래프 탐색
- 너비 우선 탐색
- 깊이 우선 탐색
2. 문제: 영역 구하기 (2583번)
- 단계: 🥈실버 1티어
- 알고리즘 분류: 그래프 이론, 그래프 탐색, 너비 우선 탐색, 깊이 우선 탐색
- 출처: https://www.acmicpc.net/problem/2583
영역 구하기
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 128 MB | 50576 | 29166 | 22684 | 57.959% |
문제
눈금의 간격이 1인 M×N(M,N≤100)크기의 모눈종이가 있다. 이 모눈종이 위에 눈금에 맞추어 K개의 직사각형을 그릴 때, 이들 K개의 직사각형의 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어진다.
예를 들어 M=5, N=7 인 모눈종이 위에 <그림 1>과 같이 직사각형 3개를 그렸다면, 그 나머지 영역은 <그림 2>와 같이 3개의 분리된 영역으로 나누어지게 된다.
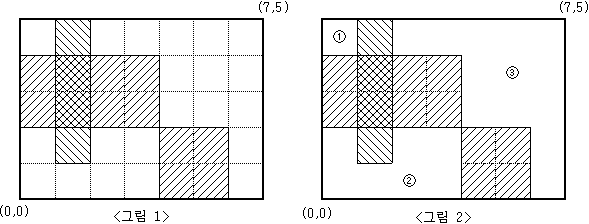
<그림 2>와 같이 분리된 세 영역의 넓이는 각각 1, 7, 13이 된다.
M, N과 K 그리고 K개의 직사각형의 좌표가 주어질 때, K개의 직사각형 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어지는지, 그리고 분리된 각 영역의 넓이가 얼마인지를 구하여 이를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 M과 N, 그리고 K가 빈칸을 사이에 두고 차례로 주어진다. M, N, K는 모두 100 이하의 자연수이다. 둘째 줄부터 K개의 줄에는 한 줄에 하나씩 직사각형의 왼쪽 아래 꼭짓점의 x, y좌표값과 오른쪽 위 꼭짓점의 x, y좌표값이 빈칸을 사이에 두고 차례로 주어진다. 모눈종이의 왼쪽 아래 꼭짓점의 좌표는 (0,0)이고, 오른쪽 위 꼭짓점의 좌표는(N,M)이다. 입력되는 K개의 직사각형들이 모눈종이 전체를 채우는 경우는 없다.
출력
첫째 줄에 분리되어 나누어지는 영역의 개수를 출력한다. 둘째 줄에는 각 영역의 넓이를 오름차순으로 정렬하여 빈칸을 사이에 두고 출력한다.
예제 입력 1 복사
5 7 3
0 2 4 4
1 1 2 5
4 0 6 2
예제 출력 1 복사
3
1 7 13
출처
Olympiad > 한국정보올림피아드 > 한국정보올림피아드시․도지역본선 > 지역본선 2006 > 고등부 2번
- 문제의 오타를 찾은 사람: alphago92
- 데이터를 추가한 사람: hjhj97
- 잘못된 데이터를 찾은 사람: kookmin20103324
알고리즘 분류
3. 나의 풀이: BFS와 DFS를 활용한 영역 구하기
오늘은 '영역 구하기' 문제를 BFS와 DFS 두 가지 방법으로 풀어보았습니다. 이 문제는 그래프 탐색을 통해 직사각형으로 나뉜 영역을 구하는 전형적인 문제로, BFS와 DFS를 통해 효율적으로 해결할 수 있습니다.
왜 DFS와 BFS가 적합한가?
이 문제는 2차원 평면에서 연결된 영역을 찾는 전형적인 문제입니다. 이 문제의 핵심은 각 영역이 연결되어 있는지를 탐색하고, 그 넓이를 계산하는 것입니다. 이러한 문제는 그래프 탐색 알고리즘인 DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)를 사용하기에 매우 적합합니다.
- 그래프 탐색 문제: 주어진 격자를 그래프의 노드로 간주하고, 인접한 노드들(즉, 상하좌우로 연결된 영역)을 탐색하는 문제입니다. 이 문제에서 직사각형을 제외한 영역들이 어떻게 연결되어 있는지를 탐색하는 것이 핵심입니다.
- 연결된 구성 요소: DFS와 BFS는 모두 연결된 구성 요소를 찾는 데 유용합니다. 한 노드(격자의 점)에서 시작해 연결된 모든 노드를 탐색하여 하나의 구성 요소로 묶을 수 있습니다. 이 문제에서 "하나의 구성 요소"는 하나의 독립된 영역을 의미합니다.
- 재귀적 탐색 또는 큐를 이용한 탐색: DFS는 재귀적 또는 스택을 사용하여 깊이 우선으로 탐색을 진행하고, BFS는 큐를 사용해 너비 우선으로 탐색합니다. 이 두 방법 모두 격자의 모든 점을 방문하면서 각 영역의 크기를 측정하는 데 유용합니다.
따라서 DFS와 BFS 알고리즘을 활용하는 것은 이 문제의 요구사항을 정확히 만족시키는 효율적인 접근 방법입니다.
1) BFS(너비 우선 탐색) 풀이
BFS는 큐를 이용해 가까운 노드부터 탐색하는 방법입니다. 다음은 BFS를 활용한 코드입니다.
import sys
from collections import deque
def bfs(x, y, grid, visited, M, N):
queue = deque()
queue.append((x, y))
visited[x][y] = True
area = 0
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
while queue:
cx, cy = queue.popleft()
area += 1
for dx, dy in directions:
nx, ny = cx + dx, cy + dy
if 0 <= nx < M and 0 <= ny < N and not visited[nx][ny] and grid[nx][ny] == 0:
visited[nx][ny] = True
queue.append((nx, ny))
return area
M, N, K = map(int, sys.stdin.readline().split())
grid = [[0] * N for _ in range(M)]
for _ in range(K):
x1, y1, x2, y2 = map(int, sys.stdin.readline().split())
for i in range(y1, y2):
for j in range(x1, x2):
grid[i][j] = 1
visited = [[False] * N for _ in range(M)]
areas = []
for i in range(M):
for j in range(N):
if grid[i][j] == 0 and not visited[i][j]:
area = bfs(i, j, grid, visited, M, N)
areas.append(area)
print(len(areas), ' '.join(map(str, sorted(areas))), sep='\\n')
코드 설명
- BFS 함수: 주어진 시작점
(x, y)에서 너비 우선 탐색을 수행해, 연결된 0 영역의 크기를area에 저장합니다. - 방문 처리: 이미 방문한 점은
visited배열에 기록해 중복 탐색을 방지합니다. - 큐 사용: 큐를 사용해 인접한 영역을 탐색하며, 큐가 빌 때까지 반복합니다.
- 결과 출력: 발견한 영역의 크기를
areas리스트에 저장하고, 정렬해 출력합니다.
시간 복잡도
- BFS는 격자의 모든 점을 한 번씩 방문합니다. 이때 각 점을 방문하고 네 방향으로 탐색하는 데 O(1)의 시간이 걸리므로, 전체 시간 복잡도는 O(M×N)입니다.
결과

2) DFS (스택을 이용한 깊이 우선 탐색) 풀이
DFS는 스택을 사용하여 깊이 우선으로 노드를 탐색하는 방법입니다. 이번에는 재귀 대신 스택을 이용한 DFS로 문제를 풀어보았습니다.
import sys
from collections import deque
def dfs_stack(x, y, grid, visited, M, N):
stack = deque()
stack.append((x, y))
visited[x][y] = True
area = 0
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
while stack:
cx, cy = stack.pop()
area += 1
for dx, dy in directions:
nx, ny = cx + dx, cy + dy
if 0 <= nx < M and 0 <= ny < N and not visited[nx][ny] and grid[nx][ny] == 0:
visited[nx][ny] = True
stack.append((nx, ny))
return area
M, N, K = map(int, sys.stdin.readline().split())
grid = [[0] * N for _ in range(M)]
for _ in range(K):
x1, y1, x2, y2 = map(int, sys.stdin.readline().split())
for i in range(y1, y2):
for j in range(x1, x2):
grid[i][j] = 1
visited = [[False] * N for _ in range(M)]
areas = []
for i in range(M):
for j in range(N):
if grid[i][j] == 0 and not visited[i][j]:
area = dfs_stack(i, j, grid, visited, M, N)
areas.append(area)
print(len(areas), ' '.join(map(str, sorted(areas))), sep='\\n')
코드 설명
- DFS 함수: 스택을 사용해 현재 노드에서 시작하는 깊이 우선 탐색을 수행합니다.
- 방문 처리: 이미 방문한 점을
visited배열에 기록해 중복 탐색을 방지합니다. - 스택 사용: 스택을 사용해 깊이 우선으로 인접한 영역을 탐색합니다.
- 결과 출력: 찾은 영역의 크기를
areas리스트에 저장하고, 정렬하여 출력합니다.
시간 복잡도
- DFS(스택)는 격자의 모든 점을 한 번씩 방문하면서 깊이 우선으로 탐색합니다. 이 과정은 O(M×N)의 시간이 소요되므로, 전체 시간 복잡도는 O(M×N)입니다.
결과

3) DFS (재귀를 이용한 깊이 우선 탐색) 풀이
마지막으로, 재귀를 이용한 DFS를 통해 문제를 해결할 수 있습니다. 재귀를 활용하면 코드가 더 간결해지지만, 깊이 제한을 설정해야 할 수도 있습니다.
import sys
sys.setrecursionlimit(10**6)
def dfs_recursive(x, y, grid, visited, M, N):
visited[x][y] = True
area = 1
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
for dx, dy in directions:
nx, ny = x + dx, y + dy
if 0 <= nx < M and 0 <= ny < N and not visited[nx][ny] and grid[nx][ny] == 0:
area += dfs_recursive(nx, ny, grid, visited, M, N)
return area
M, N, K = map(int, sys.stdin.readline().split())
grid = [[0] * N for _ in range(M)]
for _ in range(K):
x1, y1, x2, y2 = map(int, sys.stdin.readline().split())
for i in range(y1, y2):
for j in range(x1, x2):
grid[i][j] = 1
visited = [[False] * N for _ in range(M)]
areas = []
for i in range(M):
for j in range(N):
if grid[i][j] == 0 and not visited[i][j]:
area = dfs_recursive(i, j, grid, visited, M, N)
areas.append(area)
print(len(areas), ' '.join(map(str, sorted(areas))), sep='\\n')
코드 설명
- DFS 함수: 재귀적으로 깊이 우선 탐색을 수행하며, 각 호출 시 인접한 영역을 탐색합니다.
- 재귀 깊이 제한 설정:
sys.setrecursionlimit를 사용해 재귀 깊이 제한을 설정하여 무한 재귀에 빠지지 않도록 합니다. - 결과 출력: 탐색한 영역의 크기를
areas리스트에 저장하고, 정렬하여 출력합니다.
시간 복잡도
- DFS(재귀)는 스택을 사용하는 DFS와 마찬가지로, 모든 점을 한 번씩 방문하면서 깊이 우선으로 탐색합니다. 전체 시간 복잡도는 O(M×N)입니다.
결과

마무리
이번 포스팅에서는 그래프 탐색의 대표적인 두 가지 방법인 BFS와 DFS를 활용해 문제를 해결했습니다. BFS는 큐를 사용하여 너비 우선으로 탐색하며, DFS는 스택 또는 재귀를 통해 깊이 우선으로 탐색하는 방식입니다. 이 문제를 통해 두 알고리즘의 특성을 비교해 볼 수 있었고, 상황에 따라 적합한 방법을 선택하는 것이 중요하다는 점을 배울 수 있었습니다.
왜 DFS와 BFS가 이 문제에 적합한지 다시 강조하자면:
- 연결된 영역 탐색: 이 문제는 주어진 격자에서 연결된 구성 요소를 찾아 그 크기를 계산하는 문제로, 이는 DFS와 BFS의 전형적인 용도입니다.
- 그래프 탐색의 효율성: BFS와 DFS 모두 각 노드를 한 번씩만 방문하므로 시간 복잡도가 O(M×N)으로, 격자의 모든 점을 효율적으로 탐색할 수 있습니다.
- 다양한 탐색 방식 적용 가능: BFS는 모든 경로를 넓게 탐색하여 빠르게 최단 경로를 찾는 데 유리하며, DFS는 특정 깊이로 들어가면서 탐색하므로 다양한 문제 상황에 유연하게 대처할 수 있습니다.
알고리즘 학습에 있어 중요한 것은 다양한 방법으로 문제를 풀어보며, 각 방법의 장단점을 체득하는 것입니다. 오늘 문제 풀이를 통해 BFS와 DFS에 대한 이해를 더욱 깊게 할 수 있었기를 바랍니다.
계속해서 DFS/BFS 유형의 문제를 풀고있습니다. 확실히 이제 실버레벨의 감은 잡은것 같네요.
읽어주셔서 감사합니다!

어제보다 나은 개발자가 되기를…!
