9클럽 코테 스터디 40일차 입니다. 오늘은 8월 30일, 8월이 끝나가네요,,, 시간이 정말 빠르다는것을 느낍니다..

오늘 문제는 Dynamic Programming 유형의 문제입니다.

---

1. 오늘의 학습 키워드

• 동적 프로그래밍

---

2. 문제: 746. Min Cost Climbing Stairs

• 단계: Easy
• 주제: Array, Dynamic Programming
• 출처: https://leetcode.com/problems/min-cost-climbing-stairs/description/

746. Min Cost Climbing Stairs

You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.

You can either start from the step with index 0, or the step with index 1.

Return the minimum cost to reach the top of the floor.

Example 1:

Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.

Example 2:

Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: You will start at index 0.
- Pay 1 and climb two steps to reach index 2.
- Pay 1 and climb two steps to reach index 4.
- Pay 1 and climb two steps to reach index 6.
- Pay 1 and climb one step to reach index 7.
- Pay 1 and climb two steps to reach index 9.
- Pay 1 and climb one step to reach the top.
The total cost is 6.

Constraints:

• 2 <= cost.length <= 1000
• 0 <= cost[i] <= 999

---

3. 나의 풀이

이 문제를 해결하기 위해 동적 프로그래밍(dynamic programming) 방식을 사용할 수 있습니다. 목표는 계단의 각 단계까지 도달하는 데 드는 최소 비용을 계산한 후, 최종적으로 계단의 맨 위까지 도달하는 데 필요한 최소 비용을 찾는 것입니다.

문제 해결 단계:

1. 상태 정의: dp[i]를 계단의 i번째 단계에 도달하는 데 드는 최소 비용이라고 정의합니다.
2. 기본 경우:
   • dp[0]은 첫 번째 단계에 도달하는 비용으로, 이는 cost[0]입니다.
   • dp[1]은 두 번째 단계에 도달하는 비용으로, 이는 cost[1]입니다.
3. 점화식: i번째 단계에 도달하기 위해서는 i-1번째 단계나 i-2번째 단계에서 올 수 있습니다. 따라서 i번째 단계에 도달하는 비용은 현재 단계의 비용과 이전 두 단계 중 더 작은 비용을 더한 값이 됩니다:

$dp[i] = \text{cost}[i] + \min(dp[i-1], dp[i-2])$

4. 최종 답: 마지막 계단까지 도달하는 최소 비용은 마지막 단계(dp[n-1])나 그 전 단계(dp[n-2])에서 도달할 수 있으므로, 이 둘 중 작은 값을 반환합니다:

$\min(dp[n-1], dp[n-2])$

여기서 n은 계단의 총 단계 수입니다.

구현 코드:

아래는 이 문제를 해결하는 Python 코드입니다:

class Solution(object):
    def minCostClimbingStairs(self, cost):
        """
        :type cost: List[int]
        :rtype: int
        """
        n = len(cost)
        dp = [0] * n
        dp[0] = cost[0]
        dp[1] = cost[1]

        
        for i in range(2,n):
            dp[i] = cost[i] + min(dp[i-1],dp[i-2])

        
        return min(dp[n-1],dp[n-2])

예시:

cost = [10, 15, 20]
print(minCostClimbingStairs(cost))  # 출력: 15

cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
print(minCostClimbingStairs(cost))  # 출력: 6

설명:

• 첫 번째 예시에서, 가장 저렴한 방법은 15의 비용이 드는 첫 번째 단계를 시작하고 그 다음 맨 위로 점프하는 것입니다.
• 두 번째 예시에서, 가장 저렴한 방법은 비용이 1인 단계들을 밟고 올라가는 것입니다. 이를 통해 총 6의 비용으로 맨 위에 도달할 수 있습니다.

이 접근법은 아래로부터 위로 쌓아 올리는 동적 프로그래밍 방식으로, 시간 복잡도는 $O(n)$, 공간 복잡도는 $O(n)$입니다.

결과

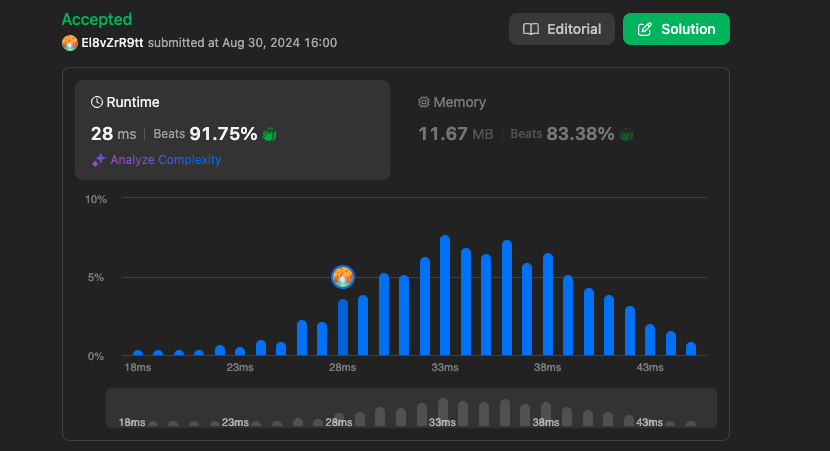
https://leetcode.com/problems/min-cost-climbing-stairs/submissions/1372970318

---

4. 다른 풀이 (메모리 효율적인 방법)

처음 구현은 이렇게 진행했는데, 주어진 변수 cost 가 있기 때문에 이것을 이용한다면 추가적인 메모리 공간을 사용하지 않고, 이것을 수정하여 최소 비용을 계산할 수 있습니다.

개선된 점:

1. 공간 복잡도 감소: 기존 코드에서는 새로운 배열 dp를 생성하여 메모리를 사용했습니다. 하지만 이 코드에서는 입력 리스트 cost를 직접 수정하기 때문에 추가적인 메모리 공간을 사용하지 않고도 결과를 계산할 수 있습니다. 따라서 공간 복잡도가 $O(1)$로 줄어듭니다.
2. 시간 복잡도 동일: 시간 복잡도는 여전히 $O(n)$입니다. 각 단계에서 이전 두 단계의 최소 비용을 계산하는 데 동일한 시간이 걸리기 때문에, 시간 측면에서는 두 코드가 동일합니다.

코드 설명:

이 코드는 cost 리스트를 직접 수정하여 최소 비용을 계산합니다. 이를 위해, 각 단계에서 이전 두 단계(i-1과 i-2)의 최소 비용을 현재 단계 비용에 더합니다. 최종적으로, 리스트의 마지막 단계(cost[n-1])와 그 전 단계(cost[n-2]) 중 더 작은 값을 반환합니다.

class Solution(object):
    
    def minCostClimbingStairs(self, cost):
        """
        :type cost: List[int]
        :rtype: int
        """
        n = len(cost)

        for i in range(2,n):
            cost[i] += min(cost[i-1],cost[i-2])

        return min(cost[n-1],cost[n-2])

요약:

이 코드가 원래 코드보다 효율적입니다. 특히, dp 배열을 따로 생성하지 않음으로써 공간 복잡도를 줄였기 때문에, 메모리 효율성이 더 좋습니다. 시간 복잡도는 두 코드 모두 $O(n)$으로 동일합니다. 따라서, 주어진 코드가 더 효율적이라고 할 수 있습니다.

결과

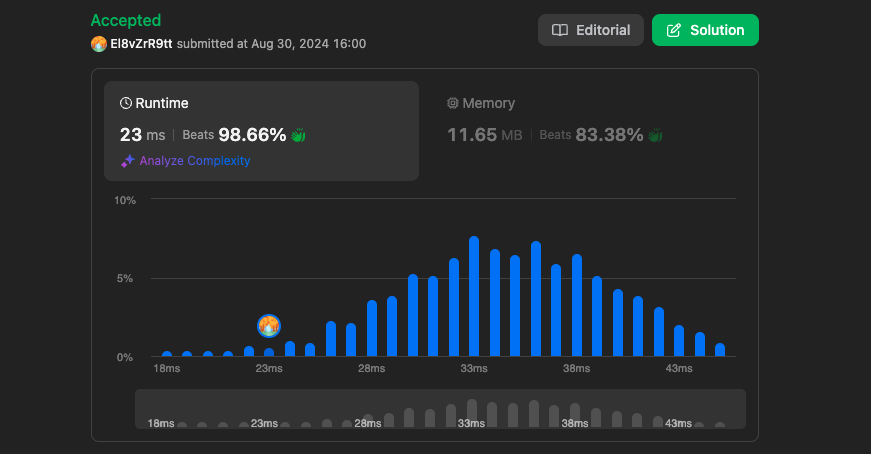
https://leetcode.com/problems/min-cost-climbing-stairs/submissions/1372970716

두 코드의 시간복잡도는 $O(n)$로 동일하지만 혹시나 해서 개인적으로 시간 측정을 진행해보았습니다.

class Solution(object):
    def minCostClimbingStairs(self, cost):
        """
        :type cost: List[int]
        :rtype: int
        """
        n = len(cost)
        dp = [0] * n
        dp[0] = cost[0]
        dp[1] = cost[1]

        
        for i in range(2,n):
            dp[i] = cost[i] + min(dp[i-1],dp[i-2])

        
        return min(dp[n-1],dp[n-2])
    def minCostClimbingStairs1(self, cost):
        """
        :type cost: List[int]
        :rtype: int
        """
        n = len(cost)

        for i in range(2,n):
            cost[i] += min(cost[i-1],cost[i-2])

        return min(cost[n-1],cost[n-2])
    
    
if __name__ == '__main__':
    
    import time
    
    t = time.time()
    
    a = Solution()
    res1 = a.minCostClimbingStairs([10,15,20])
    res2 = a.minCostClimbingStairs([1,100,1,1,1,100,1,1,100,1])
    
    print(f"Test Case1 Result: {res1}")
    print(f"Test Case2 Result: {res2}")
    
    print(f"{time.time()-t:.6f}초")
    
    
    
    t = time.time()
    
    a = Solution()
    res1 = a.minCostClimbingStairs1([10,15,20])
    res2 = a.minCostClimbingStairs1([[1,100,1,1,1,100,1,1,100,1]])
    
    print(f"Test Case1 Result: {res1}")
    print(f"Test Case2 Result: {res2}")
    
    print(f"{time.time()-t:.6f}초")

결과

Test Case1 Result: 15
Test Case2 Result: 6
0.000028초
Test Case1 Result: 15
Test Case2 Result: 6
0.000009초

공간적으로 더 효율적이다보니 시간 복잡도는 동일하지만, 실제 속도는 두 번째 코드가 더 빠른 것을 확인할 수 있습니다.

---

마무리

99클럽 코테 스터디에서 dp 알고리즘 유형은 오랜만이였습니다. 확실히 오랜만이다보니 처음에 좀 버벅였는데요. dp 알고리즘도 기업 코테에서 빈출 유형 알고리즘으로 알고있어서, 이 유형도 반복이 필요할 것으로 보입니다.

읽어주셔서 감사합니다!

더 나은 개발자가 되기를.. ! 💪