[LeetCode] 1091. Shortest Path in Binary Matrix

말하는 감자·2024년 11월 18일

BFS Graph leetcode python 리트코드 최단 경로 코딩테스트 코딩테스트 준비 파이썬

LeetCode

목록 보기

10/32

이번 문제는 그래프에서 탐색을 기반으로 최단 경로를 찾는 문제입니다.

1. 오늘의 학습 키워드

Graph
Implicit Graph
BFS

2. 문제: 1091. Shortest Path in Binary Matrix

단계: Medium
주제: Array, Breadth-First Search, Matrix
출처: https://leetcode.com/problems/shortest-path-in-binary-matrix/description/

Description

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

All the visited cells of the path are 0.
All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

Example 1:

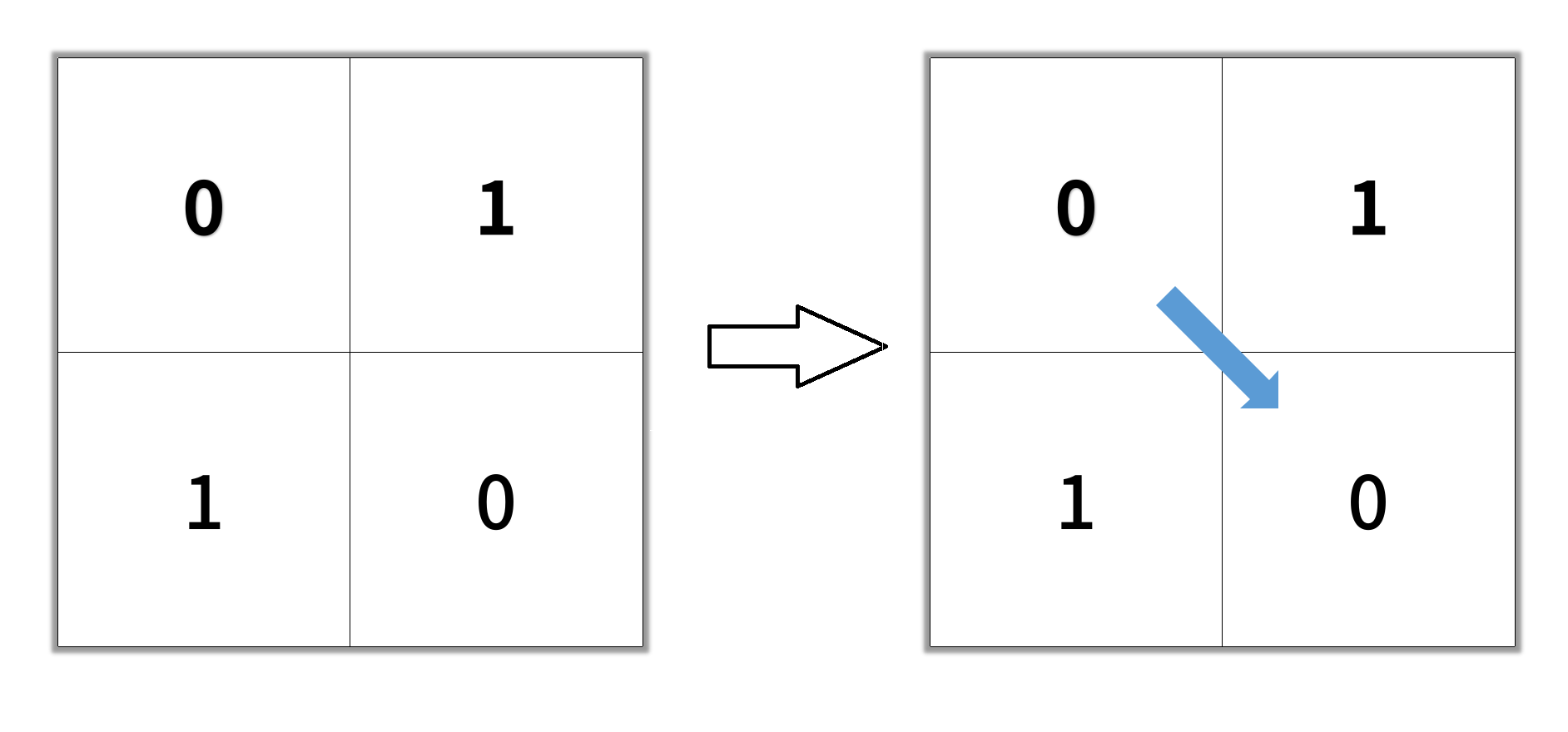
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

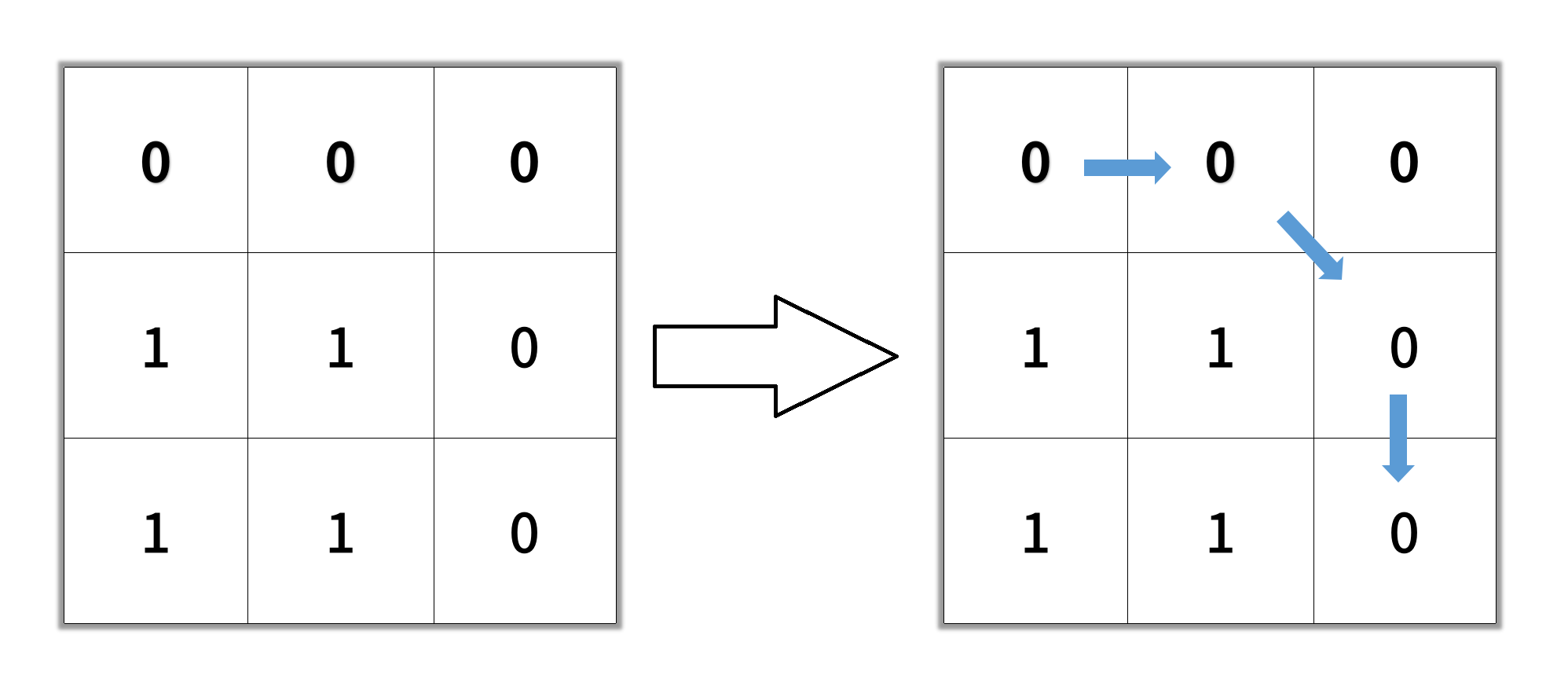
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

Constraints:

n == grid.length
n == grid[i].length
1 <= n <= 100
grid[i][j] is 0 or 1

3. 문제 풀이

n x n 이진 matrix인 grid가 주어졌을 때, 출발지에서 목적지까지 도착하는 가장 빠른 경로의 길이를 반환하는 문제입니다.

출발지는 왼쪽 위 (0,0) 위치이고 목적지는 오른쪽 아래 (n-1, n-1)위치입니다. grid에서 요소 값이 0인 cell만 지나갈 수 있으며, 8방향으로 이동이 가능합니다.

차근차근 문제 분석을 들어가보도록 하겠습니다(실제 제가 풀 때 생각한 흐름입니다).

Step1. 문제 이해하기

Input:
- 0과 1로 이루어진 이진 이차 배열로 인풋이 들어갑니다.
- row의 길이는 n, col의 길이는 n이며 n은 1과 100사이 입니다.
- 그렇다는 것은 grid의 요소 개수는 $n^2$ 으로 $10^4$ 이기 때문에 $O(n^2)$ 까지의 시간복잡도로 코드를 구현하면 될 것 같습니다. → 여기서 n은 $10^4$ 기준의 시간복잡도입니다.
- 또한, n이 1이상이므로 grid가 빈 리스트일 경우는 없다는 것을 확인할 수 있습니다.
Ouput:
- 최단 경로의 길이를 반환합니다.

해당 문제는 상하좌우, 모든 대각선 방향으로 이동이 가능합니다. 그리고 값이 0인 cell만 지나갈 수 있습니다. 그래프 순회 알고리즘을 통해 최단 경로를 구할 수 있을것 같습니다. 그래프 순회는 모든 정점을 탐색하기 때문에 이중에서 가장 짧은 길이를 선택하면 될 것입니다.

Step2. 문제 분석하기

이전 스텝에서 그래프 순회를 사용하면 문제가 해결될 것이라 짐작을 했습니다. 이번에는 실제 예시를 통해 가능한 지 확인 해보겠습니다.

우선, BFS알고리즘을 먼저 생각해보았습니다.

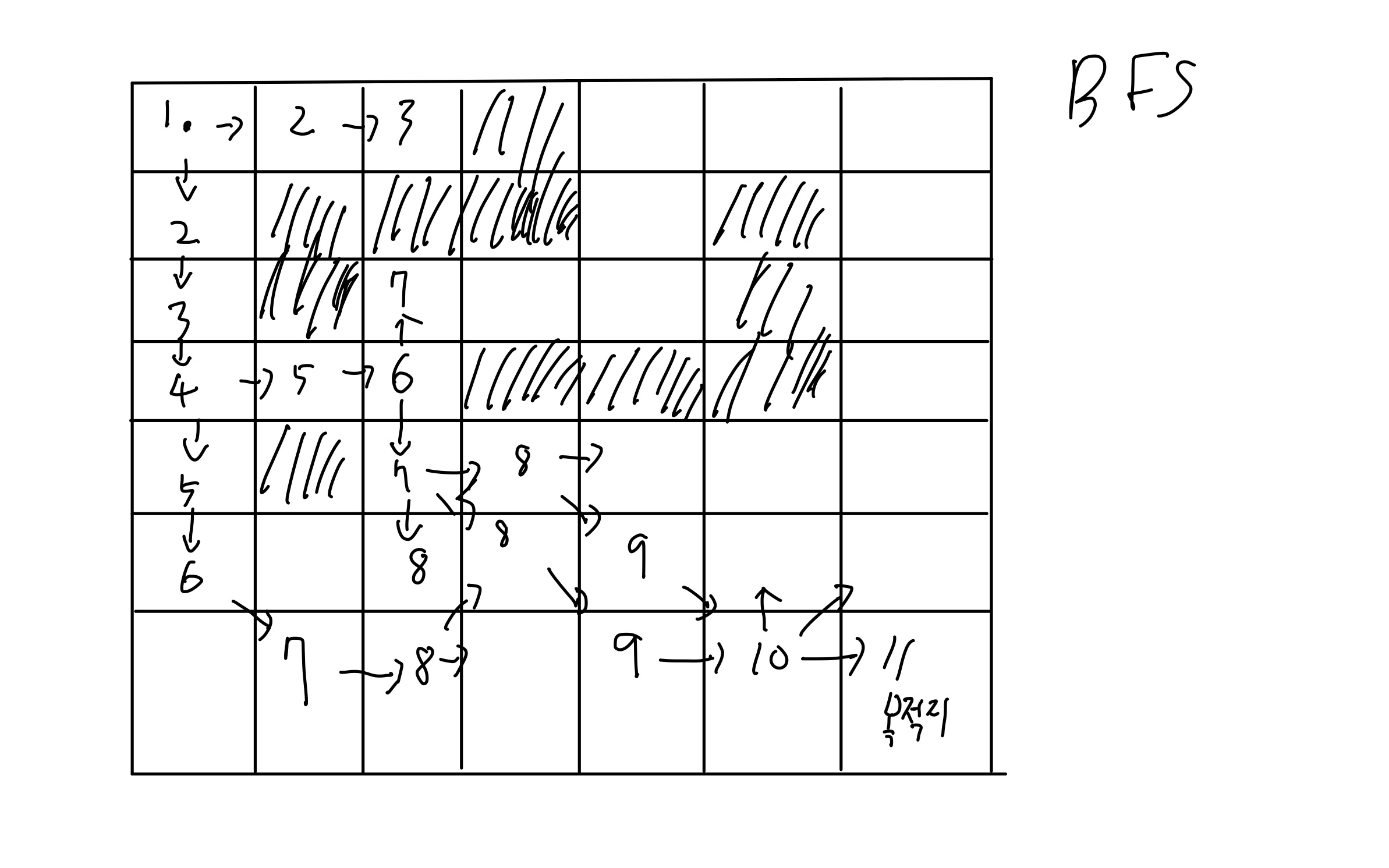
위 그림처럼 BFS알고리즘을 사용하면 쉽게 최단 경로를 바로 구할 수 있습니다. 그렇다면 DFS알고리즘은 어떨까요?

DFS알고리즘으로도 구할 수 있지만, DFS알고리즘은 잘못된 곳으로 갈 경우 다시 돌아와서 진행해야 하기 때문에 최단 경로를 구하는 문제와는 적합하지 않을 수 있습니다 (물론 가능은 합니다.)

그럼, 이제 코드 설계를 진행해보겠습니다.

Step3. 코드 설계

BFS알고리즘은 큐 자료구조를 활용합니다. 이번에는 큐 자료구조에 좌표값만 넣는것이 아니라 경로의 길이까지 넣습니다. 그 다음 8방향조건에 맞춰서 위치를 이동한 다음 그 위치가 1이 아니고, grid길이 내부에 있으면 이동하면 됩니다. 이동하면서 길이는 +1을 합니다. 방문하면 방문했다는 표시와 방문 위치 좌표를 큐 자료구조에 enqueue를 진행합니다.

Step4. 코드 구현

from collections import deque
class Solution(object):
    def shortestPathBinaryMatrix(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        directions = [(-1, 0), (1, 0), (0, -1), (0, 1), (1, 1), (1, -1), (-1, 1), (-1, -1)]

        result = -1
        m = len(grid)
        n = len(grid[0])
        if grid[0][0] != 0 or grid[m-1][n-1] != 0:
            return result
        queue = deque()
        queue.append((0,0,1))
        visited = [[False] * n for _ in range(m)]
        visited[0][0] = True

        while queue:
            cur_x, cur_y,cur_d = queue.popleft()

            if cur_x == m - 1 and cur_y == n - 1:
                result = cur_d
                break
            for dx, dy in directions:
                next_x = cur_x + dx
                next_y = cur_y + dy

                if 0 <= next_x and next_x < m and 0 <= next_y  and next_y < n:
                    if grid[next_x][next_y] == 0 and not visited[next_x][next_y]:
                        queue.append((next_x,next_y,cur_d+1))
                        visited[next_x][next_y] = True

    
        return result

코드 설명:

방향 설정
- 8방향으로 이동할 수 있으므로, 이동 가능한 모든 방향을 directions 리스트에 저장합니다:
```
directions = [(-1, 0), (1, 0), (0, -1), (0, 1), (1, 1), (1, -1), (-1, 1), (-1, -1)]
```
초기 조건 확인
- 시작점 grid[0][0] 또는 끝점 grid[m-1][n-1]이 1인 경우, 경로가 없으므로 1을 반환합니다:
```
if grid[0][0] != 0 or grid[m-1][n-1] != 0:
    return -1
```
큐 초기화
- BFS를 위해 queue를 초기화하고, 시작점 (0, 0)과 초기 경로 길이 1을 큐에 추가합니다:
```
queue = deque()
queue.append((0, 0, 1))
```
방문 배열 초기화
- 방문 여부를 확인하기 위해 visited 배열을 생성하고, 시작점을 방문 처리합니다:
```
visited = [[False] * n for _ in range(m)]
visited[0][0] = True
```

BFS 탐색

큐에서 현재 위치와 경로 길이를 꺼내서 처리합니다.

만약 현재 위치가 목적지 (m-1, n-1)라면 경로 길이를 반환합니다:


if cur_x == m - 1 and cur_y == n - 1:
    result = cur_d
    break

8방향으로 이동 가능한 모든 좌표를 계산하고, 조건을 만족하면 큐에 추가합니다:


for dx, dy in directions:
    next_x = cur_x + dx
    next_y = cur_y + dy

    if 0 <= next_x < m and 0 <= next_y < n:
        if grid[next_x][next_y] == 0 and not visited[next_x][next_y]:
            queue.append((next_x, next_y, cur_d + 1))
            visited[next_x][next_y] = True

결과 반환
- BFS가 종료되었음에도 목적지에 도달하지 못했다면 1을 반환합니다.

시간 복잡도:

탐색 범위: BFS는 모든 셀을 최대 한 번 방문하므로, 탐색 범위는 O($n^2$)입니다.
큐 연산: 큐의 각 연산(삽입 및 삭제)은 O(1)이며, 최대 $n^2$ 개의 셀이 처리되므로 큐 연산의 복잡도는 $O(n^2)$ 입니다.
총 시간 복잡도: 따라서 전체 알고리즘의 시간 복잡도는 $O(n^2)$ 입니다.