[LeetCode] 142. Linked List Cycle II

말하는 감자·2024년 12월 6일
Hash Tablealgorithmdata structureleetcodelinked listpythontwo pointer리트코드알고리즘연결 리스트자료구조코딩테스트코딩테스트 준비투 포인터파이썬해시 테이블
1

LeetCode

목록 보기
29/32
post-thumbnail

오늘 문제는 이전 문제와 매우 유사하지만 원하는 반환값이 약간 다른 문제입니다. 한 번 살펴볼까요?

1. 오늘의 학습 키워드

  • Linked List
  • Hash Table
  • Two Pointer

2. 문제: 142. Linked List Cycle II

Description

Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.

Do not modify the linked list.

Example 1:

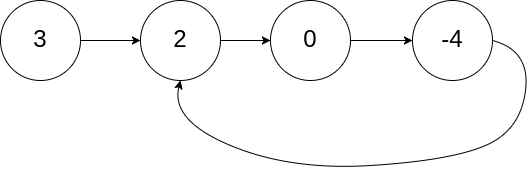
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.

Example 2:

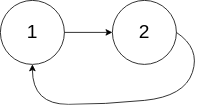
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.

Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.

Constraints:

  • The number of the nodes in the list is in the range [0, 104].
  • 105 <= Node.val <= 105
  • pos is 1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

3. 문제 풀이

Step1. 문제 이해하기

문제를 읽어보겠습니다.

문제

주어진 단방향 연결 리스트의 head가 있을 때, 사이클이 시작되는 노드를 반환하세요.

만약 사이클이 없다면 null을 반환하세요.

연결 리스트에서 사이클이란, next 포인터를 계속 따라가면 다시 방문할 수 있는 노드가 존재하는 경우를 말합니다.

내부적으로 pos는 연결 리스트의 tail(마지막 노드)이 연결된 노드의 인덱스를 나타내는데 사용됩니다(0부터 시작하는 인덱스).

만약 사이클이 없으면 pos는 -1로 설정됩니다.

참고로, pos는 함수의 파라미터로 주어지지 않습니다.

연결 리스트를 수정하지 않고 문제를 해결해야 합니다.

즉, 주어진 연결 리스트에서 사이클의 시작되는 노드를 반환하는 문제입니다.

사이클이 시작 된다는 것은 연결 리스트를 순회할 때 같은 노드가 계속해서 반복적으로 나온다는 것을 의미하기도 합니다. 저는 이 의미를 생각하자마자 Hash Table, Set을 생각했습니다. 거기다 시작노드이니 가장 먼저 반복되는 노드가 시작 노드가 될것이니까요! 우선, 입출력 조건을 통해 제가 바로 떠올린 방법이 적절한 지 살펴보도록 하겠습니다.

  • Input:
    • 연결 리스트의 노드 개수는 0이상 10410^4개 이하입니다.
      • O(n2)O(n^2)보다 효율적인 시간복잡도로 구성해야 합니다.
      • 노드가 아예 없을수도 있습니다.
    • 노드 값이 −105-10^5이상 10510^5이하입니다. 즉 노드 값이 int형에 충분히 들어갑니다. 하지만 이것이 시간 복잡도에 영향을 주지는 않습니다.
  • Output:
    • 사이클이 시작되는 노드를 반환합니다.

Step2. 문제 분석하기

Step1에서 제가 바로 찾은 방법인 Hash Table방법이 시간 복잡도 상으로도 충분히 여유가 있을것으로 보입니다.

해당 방법은 연결 리스트의 노드를 순회하면서 Hash Table에 노드값을 추가하게 됩니다. 만약, 순회 중에 hash table에 노드가 있다면 이것은 사이클의 시작노드를 의미하게 됩니다. 따라서, 총 노드 개수만큼인 o(n)o(n)의 시간 복잡도가 걸립니다.

하지만, 이 문제의 마지막 Follow up에는 다음과 같은 말이 나와있습니다

Follow up: Can you solve it using O(1) (i.e. constant) memory?

즉, 자료 구조 hash table을 사용하면 공간복잡도가 O(n)O(n)이 나옵니다. 하지만 해당 문제는 공간 복잡도를 상수로 풀 수 있냐고 물어보았습니다.

따라서, 제가 처음에 생각한 방법도 해결이 가능하지만 다른 방법을 생각해 볼 필요가 있습니다!

무엇이 있을까요?

제가 떠오른 방법은 투 포인터 방법입니다. 한 칸씩 이동하는 포인터와 두 칸씩 이동하는 포인터를 지정합니다. 포인터가 계속 이동하다 보면 만나는 구간이 있습니다. 이것이 사이클의 유무를 판별할 수 있습니다.

하지만, 그렇다고 만나는 지점이 사이클의 시작 부분은 아니게 됩니다!

예를 들어 살펴볼까요?

첫 번째 예시가 있습니다.

  • head = [3, 2, 0, -4]
  • 사이클의 시작 노드 : 2
  • 연결된 노드: 4

두 개의 포인트를 지정하고 계속해서 순회를 진행해보겠습니다.

위 그림처럼 -4 노드에서 마주하게 됩니다. 하지만 이것은 사이클의 시작 노드가 아닙니다. 따라서 이 지점에서 다시 두 포인터들을 한 칸씩 이동하다보면 같은 지점을 향하게 되는데 이것이 사이클의 시작 노드가 됩니다.

이 방법을 기반으로 사이클의 시작 노드를 알 수 있습니다.

코드 설계로 넘어가도록 하겠습니다.

Step3. 코드 설계

Hash Table Approach:

  1. 목적:
    • 각 노드를 순회하면서 이미 방문한 노드를 기록하여 첫 번째로 반복되는 노드(사이클의 시작 노드)를 반환합니다.
  2. 설계 과정:
    • node_set이라는 빈 집합(Set)을 생성합니다.
    • 현재 노드를 탐색하며, 집합에 포함되어 있는지 확인합니다:
      • 포함되어 있다면 해당 노드는 사이클의 시작점이므로 반환합니다.
      • 포함되어 있지 않다면 현재 노드를 집합에 추가합니다.
    • 연결 리스트의 끝까지 순회했는데도 반복되는 노드가 없다면 사이클이 없는 것이므로 None을 반환합니다.
  3. 특징:
    • 시간 복잡도: O(n)O(n), 노드를 한 번씩 순회.
    • 공간 복잡도: O(n)O(n), 최악의 경우 모든 노드를 집합에 저장.

Two Pointer Approach:

  1. 목적:
    • 두 포인터를 사용하여 사이클 유무를 판별하고, 사이클의 시작 노드를 반환합니다.
  2. 설계 과정:
    • 느린 포인터(slow)와 빠른 포인터(fast)를 초기화하여 head에서 시작합니다.
    • 두 포인터가 이동하며 slow는 한 번에 한 칸, fast는 한 번에 두 칸 이동합니다.
    • 두 포인터가 만날 때까지 반복합니다:
      • 만약 fast나 fast.next가 None이라면 사이클이 없으므로 None을 반환합니다.
    • 두 포인터가 만나면, slow를 head로 다시 초기화합니다.
    • 이후 두 포인터를 한 번에 한 칸씩 이동하며 다시 만나는 지점을 찾습니다:
      • 두 포인터가 만나는 지점이 사이클의 시작 노드입니다.
    • 만약 두 포인터가 다시 만나면 해당 노드를 반환합니다.
  3. 특징:
    • 시간 복잡도: O(n)O(n), 포인터가 리스트를 두 번 순회.
    • 공간 복잡도: O(1)O(1), 추가 메모리 사용 없음.

Step4. 코드 구현

Hash Table

# Definition for singly-linked list.
class ListNode(object):
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution(object):
    # 1. Hash Table
    def detectCycle(self, head):
        # https://leetcode.com/problems/linked-list-cycle-ii/submissions/1471492958
        """
        :type head: ListNode
        :rtype: ListNode
        """
        node_set = set()

        while head:
            if head in node_set:
                return head
            node_set.add(head)
            head = head.next
        return None
  • 코드 설명:
  • node_set은 각 노드를 방문하면서 저장하며, 중복된 노드를 처음 발견하면 사이클의 시작점으로 반환합니다.
  • 사이클이 없으면 while 루프를 끝까지 돌고 None을 반환합니다.
  • 시간 복잡도: O(n)O(n), 모든 노드를 한 번만 탐색.
  • 공간 복잡도: O(n)O(n), 집합에 최대 n개의 노드를 저장.
  • 결과: https://leetcode.com/problems/linked-list-cycle-ii/submissions/1471492958

Two Pointer

# Definition for singly-linked list.
class ListNode(object):
    def __init__(self, x):
        self.val = x
        self.next = None

class Solution(object):
# 2. Two Pointer
    def detectCycle(self, head):
        # https://leetcode.com/problems/linked-list-cycle-ii/submissions/1471492811
        """
        :type head: ListNode
        :rtype: ListNode
        """
        s, f = head, head

        while f and f.next:
            s = s.next
            f = f.next.next

            if s == f:
                s = head
                break
        else:
            return None
        while s!= f:
            s = s.next
            f = f.next
        return s
  • 코드 설명:
    • 두 포인터를 사용하여 사이클 유무를 확인한 후, 사이클의 시작점을 찾습니다.
    • 두 포인터가 처음 만난 후, 한 번 더 이동하면서 사이클 시작 지점을 탐색합니다.
  • 시간 복잡도: O(n)O(n), 모든 노드를 두 번 탐색.
  • 공간 복잡도: O(1)O(1), 추가 메모리 사용 없음.
  • 결과: https://leetcode.com/problems/linked-list-cycle-ii/submissions/1471492811

4. 마무리

이번 문제에서는 연결 리스트의 사이클을 탐지하고, 사이클이 시작되는 노드를 반환해야 했습니다. 두 가지 접근 방식을 통해 문제를 해결할 수 있었습니다:

  1. Hash Table 방식:
    • 직관적이고 간단하게 사이클을 탐지할 수 있습니다.
    • 각 노드를 탐색하면서 방문 여부를 Hash Table에 기록하고, 이미 방문한 노드를 발견하면 그 노드를 반환하는 방식입니다.
    • 장점: 구현이 간단하며, 사이클 탐지 및 시작 노드 반환을 빠르게 해결할 수 있습니다.
    • 단점: O(n)의 추가 메모리가 필요하여 공간 효율성이 떨어집니다.
  2. Two Pointer 방식:
    • 공간 복잡도 O(1)로 문제를 해결하는 효율적인 방법입니다.
    • 느린 포인터와 빠른 포인터를 사용해 사이클 유무를 탐지하고, 사이클의 시작 노드를 찾아 반환합니다.
    • 장점: 추가 메모리가 필요하지 않아 공간 효율적입니다.
    • 단점: 구현이 Hash Table 방식보다 다소 복잡할 수 있습니다.

이번 문제를 통해 연결 리스트의 사이클을 탐지하는 기본적인 방법과 효율성을 고려한 개선 방식을 학습했습니다. Two Pointer 방식은 다른 연결 리스트 문제에서도 자주 활용되므로 익숙해지는 것이 좋겠습니다.

전체 코드는 다음 링크에서 확인할 수 있습니다.

읽어주셔서 감사합니다!
업로드중..

profile
말하는 감자
할 수 있다
이전 포스트

[LeetCode] 24. Swap Nodes in Pairs

다음 포스트

[LeetCode] 23. Merge k Sorted Lists

0개의 댓글