[LeetCode] 743. Network Delay Time

말하는 감자·2024년 11월 25일

Graph Shortest Path dijkstra heap leetcode priority queue python 그래프 다익스트라 리트코드 우선 순위 큐 최단 경로 코딩테스트 코딩테스트 준비 파이썬 힙

LeetCode

목록 보기

15/32

오늘 문제는 가중치가 존재하는 상황에서 최단 경로를 구하는 문제입니다. 한 번 살펴볼까요?

1. 오늘의 학습 키워드

Graph
Shortest Path
Heap
Dijkstra

2. 문제: 743. Network Delay Time

단계: Medium
주제: Depth-First Search, Breadth-First Search, Graph, Heap (Priority Queue), Shortest Path
출처: https://leetcode.com/problems/network-delay-time/description/

Description

You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.

We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.

Example 1:

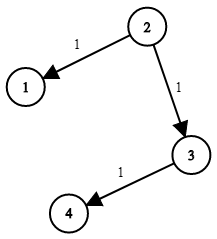
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2

Example 2:

Input: times = [[1,2,1]], n = 2, k = 1
Output: 1

Example 3:

Input: times = [[1,2,1]], n = 2, k = 2
Output: -1

Constraints:

1 <= k <= n <= 100
1 <= times.length <= 6000
times[i].length == 3
1 <= ui, vi <= n
ui != vi
0 <= wi <= 100
All the pairs (ui, vi) are unique. (i.e., no multiple edges.)

3. 문제 풀이

주어진 네트워크에는 n개의 노드가 있으며, 이는 1부터 n까지 레이블이 주어져 있습니다. 또한 $times[i] = (u_i, v_i, w_i)$ 리스트가 주어집니다. 이 리스트에서 $u_i$ 노드는 소스 노드, $v_i$ 는 타겟 노드, $w_i$ 는 $u_i$ 노드에서 신호를 보내서 $v_i$ 노드에 도달하는데 걸리는 시간을 의미합니다.

k 노드에서 신호를 보낼 때, 모든 노드에 신호가 도달하기 위한 최소 비용을 반환하시오. 하나의 노드라도 도달하지 못한다면 -1을 반환하시오. (한 노드에서 연결된 여러 개의 edge에 신호를 동시에 전달할 수 있습니다.)

문제가 길지만, 핵심만 보면 되게 직관적으로 표현이 된 문제입니다. 그럼 더 자세히 보겠습니다.

Step1. 문제 이해하기

Input:
- times 리스트가 입력으로 주어집니다. 이것의 길이는 1이상 6000이하 입니다.
- times[i]의 길이는 3이므로 무조건 source node, target node, and weight는 주어집니다.
- times 리스트의 길이가 6000, times[i]의 길이는 3이므로, 에지 개수도 1이상 6000이하 인 것을 알 수 있습니다.
- 소스 노드와 타겟 노드는 같지 않습니다. 따라서 자기 자신을 향하는 에지는 존재하지 않습니다.
- 소스 노드 $u_i$ , 타겟 노드 $v_i$ 는 1이상 n이하입니다. 즉, 문제에서 제시한대로 레이블이 1부터 n까지 주어진 그래프라 볼 수 있습니다.
- 1 ≤ k ≤ n ≤ 100 입니다. 노드는 최대 100개로 구성될 수 있습니다.
Output:
- 모든 노드에 신호가 도달하기 위한 최소 비용을 반환합니다. 하나의 노드라도 도달하지 못한다면 -1을 반환합니다.

Step2. 문제 분석하기

주어진 문제는 가중치가 있는 방향 그래프에서 단일 시작점으로부터 모든 노드에 신호가 도달하는 최소 시간을 계산하는 문제입니다. 이를 통해 특정 시작점에서 다른 노드로의 최단 경로를 찾는 알고리즘이 필요합니다.

그래프 형태:
- 그래프는 가중치가 있는 방향 그래프입니다.
- 입력은 (u, v, w) 형태로 제공되며, 이는 노드 u에서 노드 v로 가는 가중치 w의 간선이 존재함을 의미합니다.
문제의 요구사항:
- 시작 노드 k에서 출발하여 모든 노드로 신호를 전달할 수 있어야 합니다.
- 모든 노드에 도달한 후, 가장 긴 시간을 반환합니다.
- 만약 신호가 전달되지 못한 노드가 있다면 1을 반환합니다.
알고리즘 선택:
- 주어진 그래프는 가중치가 있으므로 다익스트라 알고리즘을 사용해 최단 경로를 계산할 수 있습니다.
- 다익스트라 알고리즘은 우선순위 큐(힙)를 사용하여 효율적으로 구현할 수 있으며, 시작 노드에서 다른 모든 노드로의 최단 경로를 계산하는 데 적합합니다.
복잡도 분석:
- 그래프 구성: O(E) (간선의 개수만큼 작업)
- 다익스트라 알고리즘: O(E log E) (우선순위 큐에 간선을 삽입하고 삭제하는 작업)
- 전체 복잡도: $O(E \log E + E)$ , 여기서 $E$ 는 간선의 개수, $V$ 는 노드의 개수입니다.

Step3. 코드 설계

그래프 초기화:
- 입력 데이터를 기반으로 defaultdict를 사용해 인접 리스트 형태로 그래프를 생성합니다.
- 예를 들어, (2, 3, 1)은 노드 2에서 노드 3으로 가는 가중치가 1임을 나타냅니다.
다익스트라 알고리즘 구현:
- 최소 힙(heapq)을 사용하여 노드 방문 순서를 결정합니다.
- 시작 노드 k의 가중치를 0으로 설정하고 큐에 추가합니다.
- 힙에서 노드를 하나씩 꺼내며, 해당 노드의 인접 노드를 업데이트합니다.
- 방문한 노드의 최소 비용만 저장하여 중복 방문을 방지합니다.
결과 반환:
- 모든 노드가 costs에 포함되어 있다면, costs.values()에서 최대 값을 반환합니다.
- 포함되지 않은 노드가 있다면, 1을 반환합니다.

Step4. 코드 구현

from heapq import heappush, heappop
from collections import defaultdict
class Solution(object):
    def networkDelayTime(self, times, n, k):
        # https://leetcode.com/problems/network-delay-time/submissions/1462136700
        """
        :type times: List[List[int]]
        :type n: int
        :type k: int
        :rtype: int
        """
        
        graph = defaultdict(list)
        
        for time in times:
            graph[time[0]].append((time[2], time[1]))
            
        pq = []
        heappush(pq, (0, k))
        costs = {}
        
        while pq:
            
            cur_cost, cur_node = heappop(pq)
            if cur_node not in costs:
                costs[cur_node] = cur_cost
                for cost, next_node in graph[cur_node]:
                    next_cost = cur_cost + cost
                    heappush(pq,(next_cost, next_node))
        
        for i in range(1, n + 1):
            if i not in costs:
                return - 1
            
        return max(costs.values())

코드 설명:

그래프 초기화:
- graph는 인접 리스트 형태로 생성되며, 각 노드의 간선과 가중치 정보를 저장합니다.
다익스트라 알고리즘:
- 최소 힙 pq를 사용해 가중치가 가장 작은 노드를 우선적으로 처리합니다.
- 방문하지 않은 노드만 처리하며, 최소 비용만 기록합니다.
- 현재 노드에서 인접 노드로의 이동 비용을 계산하고, 큐에 삽입합니다.
결과 계산:
- costs 딕셔너리에 n개의 노드가 모두 포함되어 있다면, 모든 노드에 신호가 도달한 것입니다.
- 이 경우, 최대 비용을 반환합니다.
- 모든 노드에 도달하지 못했다면, 1을 반환합니다.

시간 복잡도:

그래프 생성: O(E)
- 입력 데이터에서 간선 정보를 읽고 그래프를 생성하는 데 필요한 시간입니다.
다익스트라 알고리즘: O(E log E)
- 힙에 간선을 삽입하고 삭제하는 작업의 복잡도입니다.
최댓값 계산: O(n)
- 마지막으로 max(costs.values())를 호출하여 모든 노드의 도달 시간을 순회하며 최댓값을 찾습니다.
- costs는 최대 n개의 노드에 대해 도달 시간을 저장하고 있으므로 이 연산의 시간 복잡도는 $O(n)$ 입니다.
최종 복잡도: $O(E \log E)$