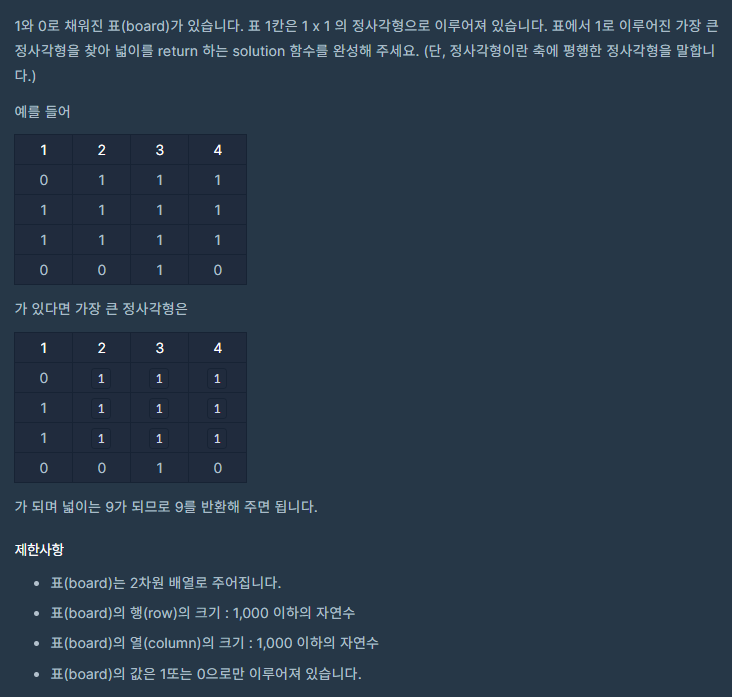
문제
들어가기 전에,
먼저 이 문제를 효율성에 맞춰서 풀기 위해서는 Dynamic Promgamming(동적 프로그래밍) 알고리즘을 사용해야한다
동적 프로그래밍 알고리즘 이란,
-
큰 케이스를 작은 케이스로 나눠서 작은 케이스들을 계속해서 검사하는
Top - Down방법과 -
작은 케이스 부터 검사하며, 큰 케이스를 작은 케이스로 부터 얻어 내는
Bottom - Up방법을 사용한다.
이것이 가능한 이유는, 동적 프로그래밍으로서 얻을 수 있는 작은 케이스들은 답이 변하지 않기 때문이다.
답이 변하지 않은 것들을 따로 저장(Memoization) 을 해서, 큰 케이스를 구할때 작은케이스를 다시 구할 필요 없이 빠르게 바로 구할 수 있다는 장점이 있다.
접근법
먼저, 각각의 행(col), 열(row) 을 순회하며 사각형을 이루는 값들을 확인한다.
가장 큰 값을 얻게 되는 경우를 생각해보자.
`[1,1][1,2][1,3][1,4][1,5]`
`[2,1][2,2][2,3][2,4][2,5]`
`[3,1][3,2][3,3][4,3][3,5]`
`[4,1][4,2][4,3][4,4][4,5]`
`[5,1][5,2][5,3][5,4][5,5]`5x5 행렬에서 가장 사각형이 되는 경우는 (5,5) 위치에 있는 행렬 기준에서 생각을 해야한다.
-
(5,5)행렬의 위치에 있는바로 위,왼쪽 옆,왼쪽 대각이 모두1을 갖고 있어아 한다. -
각각의
바로 위,왼쪽 옆,왼쪽 대각이 또한 길이를4로 하는 사각형이여야(5,5)행렬이 길이를5로 하는 사각형이 된다.2.1 각각의
바로 위,왼쪽 옆,왼쪽 대각에 해당하는 위치의바로 위,왼쪽 옆,왼쪽 대각또한, 길이를3으로 하는 사각형이여야 한다. -
2의 과정을 길이를 1로 하는 사각형일 때까지 반복한다.
이를 고려하면, NxM 행렬에서 가장 큰 사각형을 구하는 방법은, 바로 위, 왼쪽 옆, 왼쪽 대각 이 모두 같은 값을 갖을 때, 가장 큰 사각형이 된다. 이 3 개의 과정 이 모두 같지 않으면, 그 위치 에서(여태 확인한 위치까지) 가능 한 사각형의 길이는
3 개의 과정 이 모두 1이고, 현재 위치의 값이 있을때,
3 개의 과정 의 최솟값 + 1 이 된다 (현재 위치까지 고려 하기 때문에)
이를 식으로 나타내면, 아래와 같이 나타난다.
조건) 현재 위치의 값이 있을 때,
현재 위치에서 가능한 길이
= 최솟값 + 1
ㄴ (현재 위치 열 - 1, 현재 위치 행),
ㄴ (현재 위치 열 - 1, 현재 위치 행 - 1),
ㄴ (현재 위치 열, 현재 위치 행 - 1) 첫번째 행과 첫번째 열은 이전에 확인할 행 or 열 이 없기 때문에 첫번째 행과 첫번째 열은 제외하고 찾을 수 있다.
코드
def solution(board):
row_length = len(board)
col_length = len(board[0])
result = 0
for row in range(1, row_length):
for col in range(1, col_length):
if board[row][col] == 1:
if board[row - 1][col] >= 1 and board[row][col - 1] >= 1 and board[row - 1][col - 1] >= 1:
board[row][col] = min(board[row - 1][col], board[row][col - 1], board[row - 1][col - 1]) + 1
return max([x for y in board for x in y]) ** 2보통, 다이나믹 프로그래밍 을 하면, dp 를 만들어서 메모이제이션을 해주는데, 이 때는, board의 값을 검사하며 board에 저장을 해주기 때문에 따로 저장을 해주지 않아도 가능하다.