BoostCamp AI Tech 4기 논문 스터디 3회차

BPR: Bayesian Personalized Ranking from Implicit Feedback (UAI'09)

---

Abstract

• item에 대한 개인화된 순위를 예측하는 것이 item recommendation
• 이 논문은 implicit feedback의 일반화된 시나리오를 조사
  • matrix factorization(MF)나 adaptive k-nearest-neighbor(kNN)과 같은 implicit feedback 기반 item recommendation 존재
  • 이들이 개인화된 순위 예측을 하도록 설계되었지만, 그것에 직접 최적화된 방법은 없음
• 우리는 Bayesian 분석에서 도출된 최대 사후 추정량인 개인화된 순위에 대한 최적화 기준 BPR-OPT를 제안한다.
• 또한 BPR-OPT에 대해 일반적인 학습 알고리즘(LEARNBPR)을 제공한다.
  • 이는 bootstrap smapling 사용 stochastic gradient descent 기반
• 우리의 방식을 MF와 adaptive kNN에 어떻게 적용하는가 보여줄 것.
• 개인화된 순위를 정할 때는 우리의 최적화 방법이 MF와 adaptive kNN를 능가하는 성능을 보여줄 것.
  • 올바른 기준에 대해 최적화 방식이 중요하다는 점을 시사

즉, 우리는 개인화된 순위를 정할 때 필요한 기준을 최적화하는 방식인 BPR-OPT를 제안할 것이고 이것이 기존의 MF와 adaptive kNN에 어떻게 적용될 것인지, 얼만큼 성능을 낼 것인지 보여주겠다!

1. Introduction

• 컨텐츠를 추천하는 것은 많은 정보 시스템에서 중요한 작업
  • Amazon 온라인 쇼핑에서 해당 고객이 원할 것 같은 컨텐츠를 추천해주는 것
  • Youtube 비디오 포털에서 영화를 추천해주는 것
• 추천은 제공자와 손님 모두에게 도움이 되므로 매력적
• 우리는 이러한 추천에 주목을 해 보자. 이것은 아주 활발한 주제
  • item 추천이란 user 맞춤 랭킹을 만들어내는 작업
  • user의 선호는 user가 시스템과 상호작용했던 과거를 보고 배움
  • 무엇을 샀는지, 무엇을 보았는지 등등...
• 요즘 대부분 연구는 explicit feedback 기반이지만, 현실에선 implicit 상황이 대부분
  • user는 그의 취향을 explicit하게 잘 드러내지 않음
• implicit feedback은 자연스럽게 추적되므로 모으기 쉽고, 이미 대부분의 정보 시스템에서 이용가능
  • 클릭 모니터링, view 시간, 구매 등등...
  • 웹 서버가 log file에 모든 page access 기록 중
• 이 논문에서는 개인화된 순위를 위한 학습 모델의 일반적인 방법을 제시할 것.

contributions

1. 최적의 개인화된 순위를 위한 maximum posterior estimator로부터 파생된 일반적인 최적화 기준 BPR-OPT를 제안한다. ROC curve 아래 영역의 극대화를 위한 BPR-OPT 유추를 보여줄 것이다.

2. BPR-OPT의 최적화(maximizing으로 표현됨)를 위해 일반적인 학습 알고리즘 LEARNBRP을 제안할 것이다. 이것은 bootstrap sampling 사용 stochastic gradient descent 기반이다. 우리의 알고리즘이 BPR-OPT에 대한 일반적인 gradient descent 최적화 기술보다 뛰어나다는 것을 보여주겠다.

3. LEARNBRP을 two state-of-the-art 추천(MF, adaptive kNN)에 어떻게 적용하는지 보여주겠다.

4. 실험을 통해 다른 학습 방식보다 BRP을 이용한 학습 모델이 개인화된 순위 작업에 대해서는 뛰어나다는 것을 경험적으로 보여주겠다.

2. Related Work

• 가장 많이 사용되는 모델은 kNN collaborative filtering
• 이 kNN의 유사도 matrix는 전통적으로 heuristics(피어슨 상관관계 등)로 계산
• 요즘 연구는 유사도 matrix가 model parameter로서 학습의 대상이 됨
• 최근 MF가 implicit, explicit feedback 양쪽에서 널리 사용된다.
  • 초기 작업에서는 Singular Value Decomposition(SVD)가 feature matrices 학습을 위해 제안됨
  • SVD를 통해 학습된 MF 모델은 overfitting에 매우 취약하다는 단점 존재하여, 이후 정규화된 학습 방법이 제안됨
    • Hu와 그 외, Pan과 그 외 논문은 case 가중치를 사용한 정규화된 최소 제곱 최적화(WR-MF) 제안
      • case 가중치를 통해 부정적인 예시의 효과를 줄일 수 있음
    • Hofmann은 probabilistic latent semantic model 제안
    • Schmidt-Thieme는 문제를 multi-class problem으로 변환하여 binary classifiers로 해결
• 위의 연구들은 개인화된 순위 dataset으로 평가되지만, 어느것 하나 순위를 위해 직접 model parameter를 최적화하지는 않음. 순위가 일차적인 목적은 아니라는 것. 그저 어떤 item이 user에게 선택되는가 되지 않는가 예측에 대해서만 최적화
• 우리는 item 쌍 기반 개인화된 순위에 대한 최적화 기준을 끌어낸다.
  • item 쌍은 3에서 나올 $item1 >_u item2$와 같은 것을 의미
• 일반적인 학습 방식에 대비해 우리의 방식이 MF, kNN에서 어떻게 최적화하는지 보여줄 것이다.
• 더 논의할 것?
  • 우리의 접근 방식과 WR-MF의 접근 방식의 관계에 대해 (5.1에서 다룸)
  • maximum margin matrix factorization에 대해 (5.2에서 다룸)
  • 우리의 최적화 기준과 AUC 최적화의 관계(3에서 다룸)

이 논문에서는 model parameter의 offline 학습에 중점을 둔다. 학습 방식을 online으로 확장하는 것은 MF에 대한 순위 예측 관련 작업에서 연구되었기 때문에 동일하게 BPR에도 적용할 수 있다.

non-collaborative 모델로 rating을 학습하는 것과 관련된 연구도 존재한다. 한 가지 방향은 순열(permutations)에 대한 분포를 모델링 하는 것. (Burges와 그외) gradient descent를 사용해 neural network 모델을 최적화한다. 어쨌든 이 방식들은 개인화되지 않은 하나의 순위만 학습한다. 반면 우리의 모델은 개인화된 순위를 학습하는 collaborative 모델이고, 따라서 우리의 BPR 모델은 개인화되지 않은 순위의 이론적인 상한선보다 나은 성능을 경험적으로 보여준다.

관련된 연구로 수많은 모델과 방법이 존재하지만, 순위 자체를 목적으로 parameter를 최적화하는 경우는 없음. 하지만 BPR 모델은 개인화된 순위 자체를 위한 모델이고 이것이 개인화되지 않은(모든 user에게 일괄적인) 순위 예측 성능보다 좋다는 걸 증명하겠다.

3. Personalized Ranking

• item의 순위화된 list를 user에게 제공하는 것이 개인화된 순위 업무이자 item 추천
  • 온라인 쇼핑몰의 개인화된 추천 등
• implicit feedback에서 흥미로운 것은 긍정적인 관찰만 가능하다는 것
  • user-item의 관찰되지 않은 쌍은 부정적인 feedback일 수도, 단순 결측치일 수도 있음
  • 싫어해서 안 산 건가? 몰라서 안 산 건가? (지난 논문과 비슷한 맥락)
• 그럼 어떻게 user의 implicit 행동에서 순위를 추론하는 것일까?

3.1 Formalization

• $U$: 모든 user의 집합
• $I$: 모든 item의 집합
• $S$: implicit feedback
  • $S \subseteq U \times I$
  • 온라인 쇼핑몰의 구매, 비디오 포털의 재생, 웹사이트의 클릭 등
• $>_u$: 모든 item에 대한 개인화된 전체 순위(부등호로 표현)
  • $>_u \subset I^2$ 두 item 쌍에 대한 순위 비교라서 $I^2$
  • 만약 $item1$이 $item2$보다 순위가 높다면 $item1 >_u item2$로 표현
• $>_u$가 만족해야 할 특성 세 가지
  • totality: $I$에 속하는 모든 item $i$와 $j$에 대해 $i != j$이면 $i >_u j$ or($\vee$) $j >_u i$
  • antisymmetry: $I$에 속하는 모든 item $i$와 $j$에 대해 $i >_u j$ and($\wedge$) $j >_u i$이면 $i = j$
  • transitivity: $I$에 속하는 모든 item $i$와 $j$와 $k$에 대해 $i >_u j$ and $j >_u k$이면 $i >_u k$

편의를 위해 아래와 같은 정의도 함

• $I^+_u := {i \in I: (u,i) \in S}$
  해당 user $u$에 대해 implicit feedback이 나타나는 모든 쌍 $(u,i)$의 item $i$를 $I^+_u$라 함
  이 user가 관심을 표현한 item들의 집합
• $U^+_i := {u \in U: (u,i) \in S}$
  해당 item $i$에 대해 implicit feedback이 나타나는 모든 쌍 $(u,i)$의 user $u$를 $U^+_i$라 함
  이 item에 관심을 표현한 user들의 집합

(참고) $A := B$는 B를 A라고 부른다는 의미

3.2 Analysis of the problem setting

앞서 언급했듯이 implicit feedback system에서는 positive classes만 관측된다는 것이 문제이다. 빈 데이터는 negative feedback일지, 단순 결측치일지 구분할 수 없다. 그냥 다 무시하는 것이 일반적인 해법이겠지만 그렇게 했을 때 일반적인 기계학습 모델은 여기서 학습할 수 있는 것이 아무것도 없다는 게 문제이다.

보통의 item recommenders는 user의 item에 대한 개인화된 점수를 $\hat{x}_{ui}$로 표현한다. 이 점수에 따라 item의 rank가 sorting된다. 일반적인 기계학습은 training data를 만드는데, $(u,i) \in S$ 쌍에 positive class label을 붙이고, 그 외 나머지 조합에는 negative class label을 붙여서 만든다. 즉, implicit feedback이 나타났으면 positive, 나타나지 않았으면 negative로 분류한다는 의미이다. ($Figure\ \ 1$)

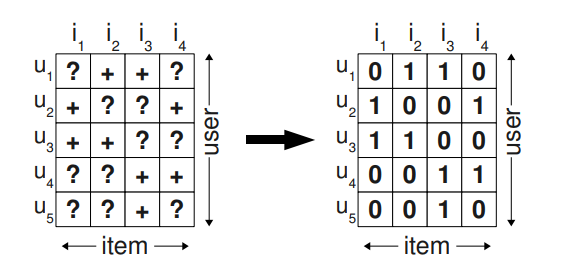
이는 위 그림처럼 $S$에 값이 있으면 1로 아니면 0으로 예측하겠다는 말이다. 문제인 것은 나중에 모델이 순위를 매겨야 할 모든 요소(지금은 값이 차 있지 않지만 나중에 채워야 할 요소)가 학습 중에 negative feedback으로 작용한다는 것이다. 이는 training data에 정확히 맞는, 충분한 표현력을 가진 모델이면 학습한 것에 따라 빈 데이터 부분을 오직 0으로만 예측할 것이기 때문에 모델이 순위를 전혀 매길 수 없게 되는 문제로 이어진다.

item 개별적인 점수 $\hat{x}_{ui}$ + implicit feedback이 발견되지 않으면 0(negative)으로?
» 모델이 점수 예측 및 순위 작업을 할 수 없게 됨

그러면 item 쌍을 training data로 사용하여 item 쌍의 순위를 최적화하는 접근을 사용해보자. implicit feedback이 존재하는 user $u$와 item $i$ 쌍 $(u,i) \in S$가 있을 때, user는 보지 않은 다른 item보다 본 적 있는 $i$를 선호한다고만 가정하자. 여기서 본 적 있다는 말은 implicit feedback이 존재한다는 의미이다. 만약 두 item 모두 user가 본 것이라면, 거기서는 둘의 어떤 선호 차이도 알 수 없는 것이다. 이를 공식으로 표현하기 위해 아래와 같은 trainig data $D_S$를 만든다.

• $D_S := {\{(u,i,j)|i \in I^+_u \wedge j \in I \backslash I^+_u}\}$
  • user $u$가 $i$는 본 적 있고, $j$는 본 적 없는 세 쌍 $(u,i,j)$를 trainig data로.
  • $i$를 $j$보다 선호한다고 볼 수 있고, negative case도 고려된다. 본 적 있는 $i$보다 본 적 없는 $j$를 더 싫어할 수 있기 때문에.

Advantages

1. positive와 negative를 모두 포함(하나는 본 거라서 positive, 다른 하나는 보지 않은 거라서 negative)한 쌍 데이터라는 것. 만약 둘 다 안 본 item 쌍이라면 그건 미래에 채워야 함. 이는 training data $D_S$와 test data가 분리되었다는 관점.

위 보통의 item recommenders는 training data의 결측치를 0으로 학습해서 test data에서도 올바른 예측을 할 수 없었지만, 여기서는 두 결측치의 관계를 채워야 할 것으로 남겨두게 되었으니 training data와 test data가 별개로 작동한다는 의미!

2. training data는 오직 순위를 위해 만들어진다. 전체 순위 $>_u$의 부분집합인 $D_s$를 training data로 사용하기 때문이다.

위에서 말했듯이 대부분의 연구는 개별화된 점수화로 item의 추천 순위를 매기는 것은 가능하긴 했어도 순위 예측을 목적으로 하는 연구는 없었음. 이것이 장점은 순위 예측 그 자체를 목적으로 한다는 것.

4. Baysian Personalized Ranking (BPR)

이제 개인화된 순위 업무를 해결하는 일반적인 방법을 끌어내보자.

• Baysian analysis: prior probability 사전확률 $p(\theta)$, likelihood function 가능도 함수 $p(i >_u j|\theta)$ 사용
• BPR-OPT: baysian analysis기반 개인화된 순위를 위한 일반적인 최적화 기준

AUC(ROC curve의 밑 넓이)와의 관계를 보여주고, BPR-OPT에 관해 모델을 학습시킬 때 LEARNBPR을 제안한다. 마지막으로 BPR-OPT와 LEARNBPR이 어떻게 MF와 kNN에 적용될 수 있는지 보여준다. 이는 기존의 학습 방법보다 더 나은 순위를 만들어낼 것이다.

4.1 BPR Optimization Criterion

Baysian analysis에서 likelihood function $p(i >_u j|\theta)$을 먼저 다루자.

올바른 개인화된 순위를 찾는 Baysian fomulation은 $\theta$가 parameter vector로 사용되는 posterior probability(사후 확률)를 최대화 하는 것이다. 아래 식은 Bayes' theorem에서 유도된다.

(참고) Bayes' theorem $P(H|E)$가 사후확률

이제 사후확률 최대화를 위해 $p(>_u|\theta)$를 키워야 한다. 여기서 $>_u$를 알고 싶지만 숨겨져 있고(최종 목표임), 모든 user들은 독립적으로 작용하고, 어떤 쌍 $(i,j)$는 다른 모든 쌍에 독립적으로 작용한다는 점에서 $p(>_u|\theta)$는 개별 density의 product로, 모든 유저의 결합으로 쓸 수 있다.

독립 조건에 의해 모든 user에 대한 $p(>_u|\theta)$는 확률 각각의 곱으로 표현되고, $D_S$에 $(u,i,j)$쌍이 있으면 b는 True로 $\delta$가 1, 없으면 $\delta$가 0으로 작용하여 해당하지 않는 항은 지워 버린다.

그 후 totality와 antisymmetry 성질(다른 두 item의 순위는 반드시 정해진다는 의미)에 의해 아래와 같이 간소화된다. 어떤 쌍 $(i,j)$는 다른 모든 쌍에 독립적으로 작용하므로 모든 순위 확률은 개별 item 쌍의 확률 곱으로 표현할 수 있는 것이다.

하지만 이것이 일반적으로 개별화된 순위 전체를 보장하지 않는 것이, totality, antisymmetry, transitivity가 충족되어야 하기 때문이다. 즉, $i_1 >_u j_1$이고 $j_1 >_u k_1$ 이면 $i_1 >_u k_1$이 되어야 하는데, 위 식은 그저 두 item 쌍이 가지는 선호 관계만 독립적으로 표현된 것이다.
그래서 아래와 같이 정의한다. ($\sigma$는 sigmoid 함수)

user $u$와 item $i$와 item $j$의 특별한 관계를 의미하는 model parameter vector $\theta$에 대한 real-valued function $\hat{x}_{uij}(\theta)$가 있다. 이는 다른 말로는 MF나 kNN의 기본적인 model class에 대한 $u, i, j$의 관계를 의미한다고 할 수 있다. 이로써 전체 순위 $>_u$를 통계적으로 정의할 수 있게 된다.

$u$가 $i$를 $j$보다 선호(implicit feedback이 i에서만 관찰)한다는 것에, $u, i, j$에 MF와 kNN에서 사용하는 model class 의미를 부여하여 관계를 형성($\theta$로 표현)하고, 그걸 sigmoid로 변형(확률은 1보다 작아야 함)한 것으로 정의하고자 하는 것 같다. MF나 kNN에는 개별적인 item 요소들이 서로 관계를 맺고 있기 때문에 그 성질만 취하는 듯? 결국 user가 본 $i$와 보지 않은 $j$를 이어주는 역할을 함

이제 Baysian analysis에서 prior probability $p(\theta)$ 다루자.

$p(\theta)$는 일반적인 prior density로, 평균이 0, 분산이 $\Sigma_\theta$인 정규분포를 따른다고 하자.

여기서 모르는 hyperparameter를 줄이기 위해 $\Sigma_\theta = \lambda_\theta I$로 두면, 이제 maximum posterior estimator를 정의할 수 있고, 이는 개인화된 순위의 일반적인 최적화 기준 BPR-OPT를 유도할 수 있다.

여기서 $\lambda_\theta$는 이 모델의 regularization parameter
잘 보면 $\ln{\sigma}$가 사용됨

$\ln$ 성질에 의해 $\prod$가 $\sum$으로 변형되는 것 주의
근데 $\lambda_\theta ||\theta||^2$ 변형은 잘 모르겠음

4.1.1 Analogies to AUC optimization

시간 없어서 여기부턴 캡쳐함 나중에 latex로 바꿈

일단 AUC에 대해서 정의

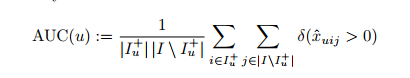
각각의 user에 대한 AUC는 위와 같이 정의. implicit feedback이 나타나지 않은 아이템인 j에 대해서 u가 i에 feedback을 나타냈고, j가 i와 관련을 맺고 있다면 true니까 델타는 1, 그렇지 않다면(즉, j는 i와 관계 없다면) 델타는 0 반환, 결국 (u,i,j)쌍이 의미를 가진다면 그들의 개수를 더하는 꼴이 됨. 그들을 공간으로 나눠 준 것이 ROC curve의 밑 면적 AUC(u)

그리고 AUC의 평균을 아래와 같이 정의

모든 유저에 대해 AUC 값을 더해주고, 모든 유저의 크기로 나눠주면 그것이 AUC의 평균일 것.

AUC(u)를 이전에 정의했던 $D_S$를 사용해 나타내면

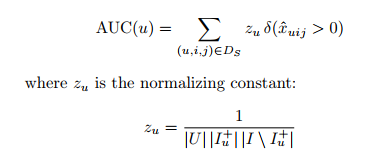
user에 대한 sigma도 포함된 $D_S$이므로 $z_u$에서 user 공간으로 나눠주는 작업도 포함
$z_u$는 normalizing constatnt.
$\delta$는 AUC에서 미분불가능한 손실함수로 사용하는데, 이는 Heaviside function(헤비사이드 계단함수)와 같음

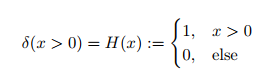
대신, 우리는 미분 가능한 함수 $\sigma(x)$ 사용할 것. AUC에 대해 최적화할 때 미분 불가능한 헤비사이드 함수를 대체하는 것이 일반적. 그것과 비슷하게 생긴 $\sigma(x)$ 와 같은 것을 사용하곤 하는데, 여기서는 $\ln{\sigma(x)}$를 사용하겠다. 그리고 이것은 MLE에서 파생된 것이다.

4.2 BPR Learning Algorithm

위에서 개인화된 순위를 위한 최적화 기준(BPR-OPT)을 도출했다. 이것은 미분가능($\ln{\sigma(x)}$를 사용했으니)하므로 gradient descent 방식을 쓰는 것이 극대화에 대해 명확한 선택일 것이다. 하지만 일반적인 gradient descent를 사용하지는 않고, bootstrap sampling에 기반을 둔 stochastic gradient descent 방식인 LEARNBPR을 사용할 것.

gradient descent를 사용할 것이니, $\theta$로 편미분하면 아래와 같음

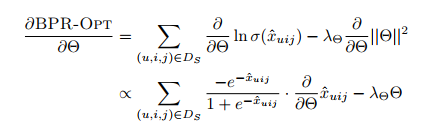
여기서 full gradient descent 방식을 쓴다고 하면, 각 step마다 모든 training data에 걸쳐 gradient가 계산되고 learning rate $\alpha$로 parameter가 업데이트 될 것.

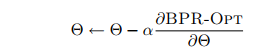
1. 이건 'correct' 방향으로 하강하지만, 수렴이 다소 느림. 우리처럼 implicit feedback 전체와 item 전체 만큼 가지고 있고, $D_S$에서 세 번 학습하는 경우에는 부적절함.
2. 그리고 training pairs에서 skewness(비뚤어짐)이 있다면 full gradient descent 방식에서 잘못된 수렴을 하게 될 수 있음. 수많은 유저 u에 대해 i는 모든 j와 비교되어야 하는데, 결국 i에 지배됨(implicit feedback을 나타낸 item i는 implicit feedback이 나타나지 않은 모든 item j에 대해 굉장히 적음. parameter $\theta$는 $u,i,j$의 관계를 의미하는데, i가 매우 적으니 i의 변화에 민감할 수밖에 없다는 의미) 결국 i를 고려하여 적은 learning rate를 설정할 수밖에 없다는 단점.
3. 그리고 gradients가 매우 다르기 때문에 regularization이 어려움

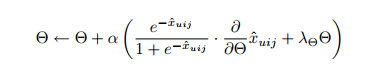
그래서 stochastic gradient descent를 사용할 것
이것은 skew problem에 적합한 방식이지만 training 쌍의 순회(traverse) 순서가 중요.
일반적인 순회 순서는 item별로 또는 user별로로 진행되지만 이는 같은 user-item 쌍에 대해 너무 많은 연속적인 업데이트를 거치게 되어 수렴 성능이 좋지 않음. (같은 user u와 i에 대해 너무나 많은 j가 존재)
이를 해결하기 위해 무작위로 3배를 선택하는 sgd 방식을 사용.
1. 그러면 연속적인 update 단계에서 똑같은 user-item 쌍을 고르는 횟수가 적어짐.
2. example 수가 너무 많고, full cycle의 일부만으로도 수렴이 가능한 경우에 효과적
관찰된 positive feedback S의 수에 따라 선형적으로 Single steps 수를 선택할 것.

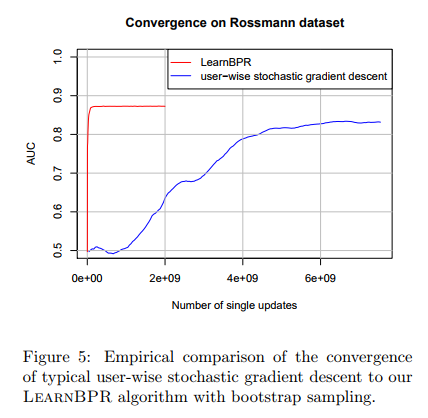
이를 보면 LEARNBPR이 user에 따라 sgd를 실행한 결과보다 훨씬 빠르게 수렴하고, AUC 값도 크다는 것을 경험적으로 알 수 있음

여기까지가 중요한 개념 설명, 이후는 적용 방법론과 이론적인 해법에 대한 이야기
앞 내용은 개념 설명이라 논문의 내용을 거의 그대로 옮겨왔지만 뒤는 방법론적인 내용이라 이해를 바탕으로 내용을 구성하여 생략된 부분이 있을 수 있음

4.3 Learning models with BPR

여기서는 두 가지 state-of-the-art model에 대해 BPR 방식으로 어떻게 학습시킬 수 있는지 다룬다. 두 모델은 Collaborative Filtering 방식인 Matrix Factorization과 Adaptive k-Nearest-Neighbor을 고른다. 이 둘은 user의 item에 대한 숨겨진 선호를 모델링 하려고 한다. 이들의 예측은 user $u$와 item $l$에 대한 실제 값 $\hat{x}_{ul}$이다.

우리의 optimization은 $(u,i,j)$에 대한 것이므로 일단 $\hat{x}_{uij}$를 분해해야 한다. 아래처럼 분해가 가능하다.

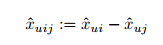
이제 두 모델을 적용하여 $\hat{x}_{ul}$를 예측한다. 다른 연구들과 동일한 CF 모델을 사용하더라도 최적화 기준은 다르다는 것을 유념해야 한다. 우리는 $\hat{x}_{ui}$ 하나를 하나의 점수로 회귀하려는 게 아니라 $\hat{x}_{ui} - \hat{x}_{uj}$ 두 개의 예측의 차를 분류하려는 것이다. 결국 목적은 순위 작업의 최적화이기 때문에 더 좋은 순위를 낼 것이다.

4.3.1 Matrix Factorization

첫 번째 CF 방식은 MF이다. user$u$의 item $i$에 대한 선호값 $\hat{x}_{ui}$ 예측은 실제 user-item matrix $X: U \times I$의 추정으로 볼 수 있음. MF를 통해 $X$는 $W$와 $H$의 product로 근사된다.

• $W = |U| \times k$
• $H = |I| \times k$
• $\hat{X} = WH^t$

W 행렬의 row는 개별 user $u$에 대한 feature vector $w_u$이고, 비슷하게 H 행렬의 row는 개별 item $i$에 대한 feature vector $h_i$이다. 위 세 가지 식에 따라 $\hat{X}$를 계산하면 아래와 같은 공식이 된다. 여기서 k는 추정의 dimensionality/rank

여기서 model parameter는 $\theta = (W,H)$이고, 관측되지 않은 user의 취향 및 user에게 관측되지 않은 item의 속성 등을 모델링하는 latent variables라고 할 수 있다.

Matrix Factorization에서 BPR 방법의 적용

최소 제곱법으로 $\hat{X}$의 $X$로의 근사는 Singular value decomposition(SVD)으로 달성된다. 하지만 머신 러닝 업무의 경우 SVD는 overfitting 때문에 다른 여러 MF 방식이 제안된다.

여기서 BPR 방법이 적용된다. 순위를 매기는 일은 BPR-OPT 기준에 대해 최적화하는 방식으로 가능하다. 또한 이는 이전에 제안한 LEARNBPR로 가능하다.

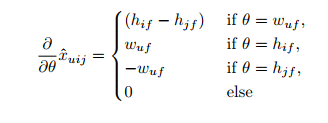
BPR Learning에 gradient descent를 사용하는 것이 옳다는 것은 4.2장에서 이미 언급하였다. 따라서 model parameter $\theta$에 대해 편미분을 하여 gradient를 구해야 하는데, 그것은 위와 같다. 우리는 $\hat{x}_{ui}$ 하나를 하나의 점수로 회귀하려는 게 아니기 때문에 parameter가 user와 item에 대한 관계를 담고 있다.

아래는 위 case에 대한 설명이다.

• parameter가 user $u$에 대한 featur vector $w_{uf}$인 경우
• parameter가 item $i$에 대한 featur vector $h_{if}$인 경우
• parameter가 item $i$에 대한 featur vector $h_{jf}$인 경우
• 그 외

여기서 regularization constants도 존재한다.

• $\lambda_W$: user feature $W$에 대한 regularization constants
• $\lambda_{H+}$: item feature $H$에 대한 regularization constants ($h_{if}$ 긍정적 업데이트)
• $\lambda_{H-}$: item feature $H$에 대한 regularization constants ($h_{if}$ 부정적 업데이트)

4.3.2 Adaptive k-Nearest-Neighbor

두 번째 CF 방식은 Adaptive kNN이다. 이것도 user $u$의 item $i$에 대한 선호값 $\hat{x}_{ui}$ 예측을 하는 것이 목표이다.

• CF에서 가장 인기있는 방식(item-based-좋은 성능 / user-based)
• 모든 다른 item과 item $i$의 유사성에 기반하여 예측
  • user $u$가 item $i$를 선호할까? ($\hat{x}_{ui}$?) $I^+_u$의 item들과 $i$의 유사성을 계산하자.
  • $I^+_u$에서 k개의 item만 고려되면 k-Nearest-Neighbor인 것
    
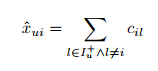
• $C : I \times I$ 이는 item 유사도 매트릭스로, $c_{il}$은 $i$와 $j$의 유사도를 의미한다.

kNN에서 model parameter $\theta$는 $C$이기 때문에 이것이 결정되면, 위의 연산이 가능해진다. 그럼 $C$는 어떻게 결정할까?

가장 일반적인 방법은 cosine vector 유사성 heuristic을 사용하는 것이다. 이로써 C를 계산하는 것이 가능해진다.

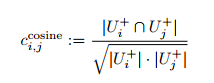
다만 이보다 더 나은 방식은 직접 계산하기보다 C 자체를 학습의 대상으로 두는 것이다. 즉, parameter로 C를 사용하여 직접 학습하는 것이다. 물론 item이 매우 많을 경우 HH^t로 분해한 것을 학습하는 방식도 있긴 하지만 이 논문에서는 C를 parameter로 두는 방식을 사용한다.

Adaptive k-Nearest-Neighbor에서 BPR 방법의 적용

이제 BPR 방법이 사용된다. BPR을 적용하여 model parameter C에 대해 BPR 최적화 기준과 LEARNBPR 알고리즘을 사용하여 kNN을 최적화할 것이다. MF의 경우와 마찬가지로 parameter $\theta$에 대해 편미분하여 gradient를 구해야 한다. 그러면 다음과 같다.

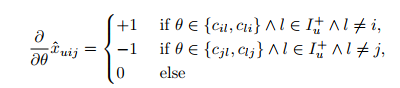
위 parameter case를 풀어서 설명하면 다음과 같다. 우리는 $\hat{x}_{ui}$ 하나를 하나의 점수로 회귀하려는 게 아니기 때문에 parameter가 user와 item에 대한 관계를 담고 있다.

• parameter가 implicit feedback이 있는 $l$과 서로 다른 $i$에 대해 $c_{il}$이거나 $c_{li}$인 경우
• parameter가 implicit feedback이 있는 $l$과 서로 다른 $j$에 대해 $c_{jl}$이거나 $c_{lj}$인 경우

여기서 regularization constants도 존재한다.

• $\lambda_+$: $c_{il}$을 업데이트할 때의 regularization constants
• $\lambda_-$: $c_{il}$을 업데이트할 때의 regularization constants

4.3을 요약하면, 기존에 사용하던 CF 모델인 MF와 Adaptive kNN에 대해서도 parameter를 설정하고, BPR 방식으로 최적화한다면 우리의 목적인 개인화된 순위를 정하는 데에 사용될 수 있다는 것을 수식적으로 설명한 것이다.

5. Relations to other methods

여기서는 제안된 BPR 방식과, 다른 두 item 예측 모델이 어떤 관계를 가지는지 얘기한다.

5.1 Weighted Regularized Matrix Factorization (WR-MF)

• Pan과 그 외, Hu와 그 외 논문은 MF를 implicit feedback 기반 item 예측에 제안
• 4.3.1에서 $\hat{X} = WH^t$, $W = |U| \times k$, $H = |I| \times k$은 동일하지만 최적화 기준과 학습 방식이 BPR-OPT, LEARNBPR과는 다름
• 여기서는 square-loss를 최소화하는 SVD를 사용하고 아래와 같은 특징이 있음
  • overfitting 방지 regularization 사용
  • positive feedback의 영향을 증가시키기 위한 loss function의 가중치 사용

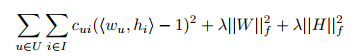
위 식에서 $c_{ui}$는 parameter가 아니다. 아래와 같이 정해진 값

• Hu: positive feedback은 추가 정보를 통한 값, 나머지는 $c_{ui} = 1$
• Pan: positive feedback은 $c_{ui} = 1$, 나머지는 1보다 작은 어떤 상수

또한 BPR과의 차이점이 존재

• BPR처럼 2개 item 쌍이 아닌 단일 item에 대한 최적화
• MLE를 사용 (그러나 item 예측은 회귀가 아닌 분류 문제라서 logistic이 어울림)
• non-positive에도 $c_{ui}$가 일정하다면 $O(iter(|S|k^2 + k^3(|I| + |U|)))$에서 학습

5.2 Maximum Margin Matrix Factorization (MMMF)

• Weimer와 그 외는 ordinal(첫째, 둘째...) 순위에 Maximum Margin Matrix Factorization (MMMF)를 제안
• 이는 explicit feedback을 위해 만들어진 시나리오
• 하지만 관찰되지 않은 item에 0 등급, 관찰된 item에 1 등급을 부여하여 사용 가능

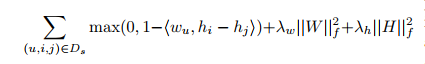
위 최적화 기준은 MF에 적용된 BPR에 상당히 유사하지만 BPR과는 차이가 존재한다.

• Error function이 다르고, BPR의 error function (hinge loss)는 smooth하다.
• BPR은 다른 여러 모델에도 적용이 가능하지만, 이것은 특정 MF에만 가능하다.

또한 학습 방식에도 차이가 있는데, 이는 원래 결측치가 많은 explicit data에 작동하도록 설계되어 implicit 설정에서보다 훨씬 적은 쌍을 가진 것으로 가정한다. 하지만 implicit에 적용할 경우 data를 조밀화(등급 채워 넣기)하고 training 쌍 $D_S$의 수가 $O(|S||I|)$에 있다(bootstrap으로 뽑아옴).

그러니까, 순위 예측을 하는 다른 모델들이 사용하는 방식이 있긴 한데, 이 논문에서 제시한 BPR과는 확실한 차이가 있다는 것을 말함

6. Evaluation

• 두 가지 인기있는 모델 MF와 kNN을 선택하여 BPR과 비교
• MF
  • URP, PLSA 등 다른 모델에 비해 높은 성능을 내는 것으로 알려져 있음
  • SVD-MF, WR-MF, 그리고 BPR-MF가 학습 방법
• kNN
  • 기존 유사도 계산 방법 Cosine-kNN과 BPR-kNN을 비교
• 각 item에 사용자 독립적인 가중치를 부여하는, 가장 인기있는 baseline을 제시
  $\hat{x}^{\mathrm{most-pop}}_{ui} := |U_i^+|$ (item i에 implicit feedback을 나타낸 모든 user의 크기)
• 개인화되지 않은 순위 방식에서 AUC의 이론적인 상한선 제시

6.1 Datasets

• 서로 다른 두 앱의 datasets 활용
• $Rossmann$ online shop
  • 10,000 users, 4000 items에 대한 426,612 건의 구매 기록
  • user가 다음에 사고 싶어하는 개인화된 list를 예측하자
• $Netflix$ DVD rental
  • 1부터 5까지의 explicit한 user 별점, 별점 기록만 제거하여 implicit 활용
  • user가 영화를 평가할 가능성이 있는지 예측하는 문제
  • 평가될 가능성이 가장 높은 영화부터 개인화된 순위 list를 만들자
  • 다만 10,000 users, 5000 item에 대한 565,738 별점 기록에서 하위 sample 제작
  • 각 user는 최소 10개의 item, 각 item은 최소 10명의 user 기록 가지도록

6.2 Evaluation Methodology

• 각 user의 기록에서 user-item 행동 하나를 무작위로 제거하여 $S_{train}$ 생성
• $S_{train}$로 학습하고, AUC를 사용하여 $S_{train}$로 평가

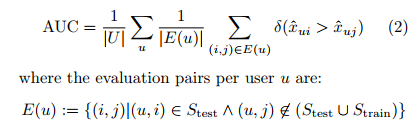
• 높은 AUC 값은 좋은 성능을 의미 (최소 0.5부터 최대 1)
• 10번의 실험을 반복(train, test set을 계속 새롭게 나눔)
  • 이 때, hyperparameter는 첫 실험에서 grid search를 통해 찾은 최적화된 값을 계속 사용

6.3 Results and Discussion

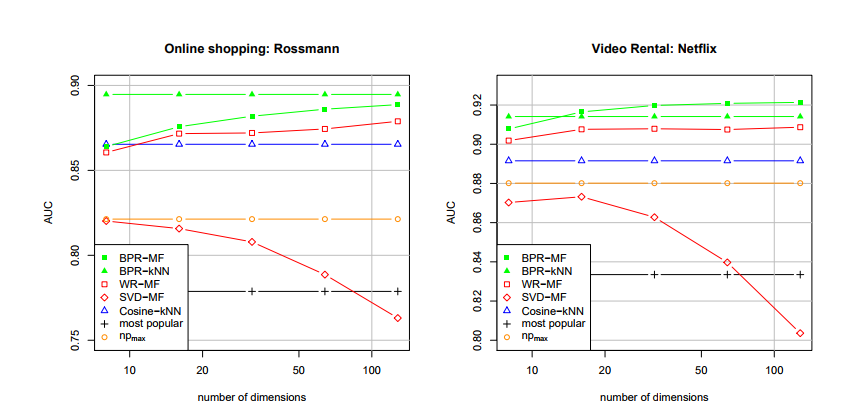
• 두 가지 dataset 모두에서 BPR-MF, BPR-kNN이 다른 모델보다 좋은 성능
• 동일한 모델(MF)을 사용한다고 해도 최적화 방법에 따라 예측 성능 차이가 확연함
  • SVD-MF는 training data에는 가장 잘 맞지만 overfitting을 초래하여 좋지 않음
    실제로 차원이 증가할수록 SVD-MF의 성능은 떨어짐
  • WR-MF는 regularization으로 차원이 증가함에 따라 성능이 꾸준히 상승
  • 8 dimensions에서 BPR-MF는 128 dimensions에서 WR-MF의 최적화 성능과 비등함
  • 따라서 BPR-MF는 확실히 WR-MF를 능가
• 요약
  • 올바른 기준에 따라 model parameter를 최적화하는 것은 중요하다.
  • implicit feedback으로부터 개인화된 순위를 예측하는 것에 대해 BPR-OPT 기준에 따라 LEARNBPR로 학습한 경우 다른 모델 및 방법보다 좋은 성능을 낸다.

6.4 Non-personalized ranking

• AUC의 비교를 통해 개인화된 순위 방법과 가장 좋은 개인화되지 않은(non-personalized) 순위 방법을 비교한다.
  • 개인화되지 않은 순위 방법은 모든 user에게 동일한 순위 $>$를 생성
  • 개인화되지 않은 순위 방법의 이론적인 상한선인 $np_{max}$를 계산
  • 가장 단순한 개인화된 방법인 Cosine-kNN이 $np_{max}$를 상회하고 즉, 개인화되지 않은 방법들의 성능을 상회

7. Conclusion

• 개인화된 순위에 대해 일반적인 최적화 기준(BPR-OPT)과 학습 알고리즘을 제안
• BPR-OPT는 Bayesian analysis로부터 파생된 maximum posterior estimator
• BPR-OPT에 관한 일반적인 학습 알고리즘으로 LEARNBPR 제안
  • 이는 bootstrap sampling 사용 stochastic gradient descent 기반
• BPR-OPT가 MF와 adaptive kNN에 어떻게 적용되는지도 보여 줌
  • 개인화된 순위 작업에서 BPR 기준으로 학습한 모델은 타 기준을 사용할 때보다 좋은 성능

결론적으로, 예측의 질은 모델뿐 아니라 최적화 기준에도 크게 영향을 받는다는 결과를 도출하게 되었다. 따라서 이론적으로, 경험적으로 BPR 최적화 방식은 중요한 개인화된 순위 작업에 올바른 선택이라고 할 수 있다.