네이버 부스트캠프 AI Tech 4기 선형대수학 스터디 1회차

선형대수학 이상구 저 Chapter1

---

1. 벡터(Vectors)

• 크기와 방향을 모두 가지는 것
• 3차원 공간의 벡터 이해 $\rightarrow$ $n$차원 공간으로 확장
• 내적과 직선 및 평면의 방정식 이해

1.1 공학과 수학에서의 벡터: $n$-공간

• 스칼라(scalar): 크기만으로 완전히 표현
• 벡터(vector): 크기와 방향이 있어야 완전히 표현
  • 시작점 $A$로부터 끝점 $B$까지 벡터 $\mathrm{x} = \overrightarrow{AB}$
  • 시작점과 끝점이 같으면 크기가 0인 영벡터
  • 크기는 같지만 방향이 완전히 반대인 벡터는 음벡터 $-\mathrm{x}$

정의 [벡터의 덧셈과 스칼라배]

• 두 벡터의 합 $\mathrm{x} + \mathrm{y}$는 $\mathrm{x},\ \mathrm{y}$에 의해 결정되는 평행사변형의 대각선으로 표시되는 벡터
• $k\mathrm{x}$는 길이에 $|k|$배 하여 결정되는 벡터, $k > 0$이면 같은 방향, $k < 0$이면 반대 방향, 0이면 영벡터

• 벡터는 크기와 방향이 같으면, 시작점 및 끝점에 관계없이 항상 동일한 벡터
• 따라서 벡터의 원점을 시작점으로 고정하였을 때, 점의 좌표를 나타낼 수 있음
  • 이에 따라 영벡터는 원점을 나타내는 것

정의

• 평면 벡터(vector in plane)는 두 실수의 순서조로 나타낼 수 있음
• $\mathrm{x} = (x_1,\ x_2) =\begin{vmatrix} x_1\\ x_2\end{vmatrix}$
• 두 실수 $x_1,\ x_2$는 평면 벡터 $\mathrm{x}$의 성분(component)
• 동일한 두 성분 값을 가지는 서로 다른 두 벡터는 상등 $\mathrm{x} = \mathrm{y}$

• 만약 시작점이 원점이 아닌 평면 벡터를 다루는 경우
  • $P(x_1,\ x_2)$가 시작점, $Q(y_1,\ y_2)$가 끝점이면
  • $\overrightarrow{PQ} = \overrightarrow{OQ'} = (y_1 - x_1,\ y_2 - x_2)$

정의

• $\mathrm{x} = \begin{vmatrix} x_1\\ x_2\end{vmatrix}$와 $\mathrm{y} = \begin{vmatrix} y_1\\ y_2\end{vmatrix}$와 $k$에 대해 아래와 같음
  • $\mathrm{x} + \mathrm{y} = \begin{vmatrix} x_1 + y_1\\ x_2 +y_2\end{vmatrix}$, $k\mathrm{x} = \begin{vmatrix} kx_1\\ kx_2\end{vmatrix}$
  • 성분은 같은 성분끼리 연산, 실수는 성분 각각에 그대로 실수 연산

• 이제 3차원 벡터로 확장이 가능

정의

• 공간 벡터(vector in space)는 세 실수의 순서조로 나타낼 수 있음
• $\mathrm{x} = (x_1,\ x_2,\ x_3)= \begin{vmatrix} x_1\\ x_2\\ x_3\end{vmatrix}_{3 \times 1}$
• 세 실수 $x_1,\ x_2,\ x_3$는 공간 벡터 $\mathrm{x}$의 성분(component)
• 동일한 세 성분 값을 가지는 서로 다른 두 벡터는 상등 $\mathrm{x} = \mathrm{y}$

• 만약 시작점이 원점이 아닌 공간 벡터를 다루는 경우
  • $P(x_1,\ x_2,\ x_3)$가 시작점, $Q(y_1,\ y_2,\ y_3)$가 끝점이면
  • $\overrightarrow{PQ} = \overrightarrow{OQ'} = (y_1 - x_1,\ y_2 - x_2,\ y_3 - x_3)$

정의

• $\mathrm{x} = \begin{vmatrix} x_1\\ x_2\\ x_3\end{vmatrix}$와 $\mathrm{y} = \begin{vmatrix} y_1\\ y_2\\ y_3\end{vmatrix}$와 $k$에 대해 아래와 같음
  • $\mathrm{x} + \mathrm{y} = \begin{vmatrix} x_1 + y_1\\ x_2 +y_2\\ x_3 + y_3\end{vmatrix}$, $k\mathrm{x} = \begin{vmatrix} kx_1\\ kx_2\\ kx_3\end{vmatrix}$
  • 성분은 같은 성분끼리 연산, 실수는 성분 각각에 그대로 실수 연산

• 이제 $n$차원 벡터로 확장이 가능
• 모든 $n$차원 전체의 집합은 $n$-공간($n$차원 공간) $\mathbb{R}^n$
  • 5차원이면, $\mathbb{R}^5$

정의

• $n$차원 벡터($n$-dimensional vector)는 $n$개 실수의 순서조로 나타낼 수 있음
• $\mathrm{x} = (x_1,\ x_2,\ ...,\ x_n) = \begin{vmatrix} x_1\\ x_2\\ \vdots\\x_n\end{vmatrix}_{n \times 1}$
• 세 실수 $x_1,\ x_2,\ x_3$는 공간 벡터 $\mathrm{x}$의 성분(component)
• 동일한 $n$개 성분 값을 가지는 서로 다른 두 벡터는 상등 $\mathrm{x} = \mathrm{y}$

정의

• $\mathrm{x} = \begin{vmatrix} x_1\\ x_2\\ \vdots\\x_n\end{vmatrix}$와 $\mathrm{y} = \begin{vmatrix} y_1\\ y_2\\ \vdots\\y_n\end{vmatrix}$와 $k$에 대해 아래와 같음
  • $\mathrm{x} + \mathrm{y} = \begin{vmatrix} x_1 + y_1\\ x_2 +y_2\\ x_3 + y_3\\\vdots\\x_n + y_n\end{vmatrix}$, $k\mathrm{x} = \begin{vmatrix} kx_1\\ kx_2\\ \vdots\\kx_n\end{vmatrix}$
  • 성분은 같은 성분끼리 연산, 실수는 성분 각각에 그대로 실수 연산

• 벡터를 정의했으니, 벡터의 결합을 정의하는 것이 가능

정의

• $\mathrm{v}_1,\ \mathrm{v}_2,\ ...,\ \mathrm{v}_k$는 $\mathbb{R}^n$의 벡터, $c_1,\ c_2,\ ...,\ c_k$는 실수
• $\mathrm{x} = c_1\mathrm{v}_1 + c_2\mathrm{v}_2 + \dots + c_k\mathrm{v}_k$를 $\mathrm{v}_1,\ \mathrm{v}_2,\ ...,\ \mathrm{v}_k$의 일차결합(linear combination)이라 함

• 벡터의 성질에 대한 정리
  (1) $\mathrm{x} + \mathrm{y} = \mathrm{y} + \mathrm{x}$
  (2) $(\mathrm{x} + \mathrm{y}) + z = \mathrm{x} + (\mathrm{y} + \mathrm{z})$
  (3) $\mathrm{x} + 0 = \mathrm{x} = 0 + \mathrm{x}$
  (4) $\mathrm{x} + (-\mathrm{x}) = 0 = (-\mathrm{x}) + \mathrm{x}$
  (5) $k(\mathrm{x} + \mathrm{y}) = k\mathrm{x} + k\mathrm{y}$
  (6) $(h + k)\mathrm{x} = h\mathrm{x} + k\mathrm{x}$
  (7) $(hk)\mathrm{x} = h(k\mathrm{x})$
  (8) $1\mathrm{x} = \mathrm{x}$
  (9) $0\mathrm{x} = 0$
  (10) $k\mathrm{0} = \mathrm{0}$
  (11) $(-1)\mathrm{x} = -\mathrm{x}$
  

1.2 내적과 직교

정의

• $\mathbb{R}^n$의 벡터 $\mathrm{x} = (x_1,\ x_2,\ ...,\ x_n)$에 대해
  $||\mathrm{x}|| = \sqrt{x_1^2 + x_2^2 + \dots + x_n^2}$
  를 $\mathrm{x}$의 노름(norm, length, magnitude)이라 함
• 이는 원점으로부터 $P(x_1,\ x_2,\ ...,\ x_n)$에 이르는 거리로 정의
• $||\mathrm{x} - \mathrm{y}||$는 $\mathrm{x},\ \mathrm{y}$가 표현하는 두 점 사이의 거리

정의

• $\mathbb{R}^n$의 벡터 $\mathrm{x} = (x_1,\ x_2,\ ...,\ x_n),\ \mathrm{y} = (y_1,\ y_2,\ ...,\ y_n)$에 대해
  $x_1y_1 + x_2y_2 + \dots + x_ny_n$
  를 $\mathrm{x},\ \mathrm{y}$의 내적(Eucilidean inner product, dot product)이라 함
• 내적은 $\mathrm{x}\cdot \mathrm{y}$으로 나타냄
• $\mathrm{x}\cdot \mathrm{y} = x_1y_1 + x_2y_2 + \dots + x_ny_n$
• $\mathrm{x}\cdot \mathrm{x} = ||\mathrm{x}||^2$

• $\mathbb{R}^n$ 벡터 $\mathrm{x},\ \mathrm{y},\ \mathrm{z}$와 스칼라 $k$에 대한 정리
  (1) $\mathrm{x}\cdot \mathrm{x} \ge 0,\ \ \mathrm{x}\cdot \mathrm{x} = 0 \Leftrightarrow \mathrm{x} = 0$
  (2) $\mathrm{x}\cdot \mathrm{y} = \mathrm{y} \cdot \mathrm{x}$
  (3) $(\mathrm{x} + \mathrm{y}) \cdot \mathrm{z} = \mathrm{x} \cdot \mathrm{z} + \mathrm{y} \cdot \mathrm{z}$
  (4) $(k\mathrm{x}) \cdot \mathrm{y} = \mathrm{x} \cdot (k\mathrm{y}) = k(\mathrm{x} \cdot \mathrm{y})$
  (5) 코시 슈바르츠 부등식 $|\mathrm{x}\cdot \mathrm{y}| \le ||\mathrm{x}||\ ||\mathrm{y}||$ (등호는 $\mathrm{x},\ \mathrm{y}$ 중 하나가 다른 것의 실수배일 때만)
  

정의

• $\mathrm{x}\cdot \mathrm{y} = ||\mathrm{x}||\ ||\mathrm{y}||\cos{\theta},\ 0 \le \theta \le \pi$인 $\theta$를 $\mathrm{x},\ \mathrm{y}$가 이루는 각(angle, 사잇각)이라 함
• $\mathrm{x}\cdot \mathrm{y} = 0$이면, $\mathrm{x},\ \mathrm{y}$는 서로 직교
  • 직교 판단은 두 벡터의 내적이 0이 되는가?
• $\mathrm{x} = k\mathrm{y}$이면, $\mathrm{x},\ \mathrm{y}$는 평행

정의

• $||\mathrm{x}|| = 1$인 벡터를 단위벡터(unit vector)라 함
• $\mathrm{x},\ \mathrm{y}$가 직교한다면, 이 벡터들을 직교(orthogonal)벡터라 함
• $\mathrm{x},\ \mathrm{y}$가 직교하면서 각각 단위벡터이면, 정규직교(orthonormal)벡터라 함

• 삼각부등식 정리
  $||\mathrm{x} + \mathrm{y}|| \le ||\mathrm{x}|| + ||\mathrm{y}||$
  등호는 $\mathrm{x},\ \mathrm{y}$ 중 하나가 다른 것의 실수($\ge 0$)배일 때만

정의

• 0벡터가 아닌 임의의 벡터 $\mathrm{x}$에 대해
  $\mathrm{u} = {1 \over ||\mathrm{x}||}\mathrm{x}$
  는 단위벡터이고, $\mathbb{R}^n$의 단위벡터 중 $n$개의 벡터
  $\mathrm{e}_1 = (1,0,0,\dots,0),\ \mathrm{e}_2 = (0,1,0,\dots,0),\ \dots,\ \mathrm{e}_n = (0,0,0,\dots,1)$
  을 기본단위벡터(standard unit vector, 표준단위벡터)라 함

• 이로써 $\mathrm{x} = x_1\mathrm{e}_1 + x_2\mathrm{e}_2 + \dots + x_n\mathrm{e}_n$로 나타내는 게 가능
• $\mathbb{R}^2$, $\mathbb{R}^3$에서는 $\mathrm{e}_1,\ \mathrm{e}_2,\ \mathrm{e}_3$ 대신 $i,\ j,\ k$를 사용

1.3 직선과 평면의 벡터방정식

직선의 방정식: 기울기(방향벡터)와 한 점

• 한 점 $P_0(x_0,\ y_0,\ z_0)$를 지나고 영벡터가 아닌 벡터 $\mathrm{v} = a\mathrm{i} + b\mathrm{j} + c\mathrm{k} = (a,\ b,\ c)$에 평행한 직선

• 이 직선이 나타내는 것은 점 $P(x,\ y,\ z)$의 집합

• 벡터방정식 ($\overrightarrow{OP} = \mathrm{p},\ \overrightarrow{OP}_0 = \mathrm{p}_0$)

  $(x,\ y,\ z) = \mathrm{p} = \mathrm{p}_0 + t\mathrm{v} = (x_0,\ y_0,\ z_0) + t(a,\ b,\ c)$

• 매개방정식 (매개변수인 $t$로 표현)

  $x = x_0 + ta,\ y = y_0 + tb,\ z = z_0 + tc$

• 대칭방정식

  ${x - x_0 \over a} = {y - y_0 \over b} = {z - z_0 \over c}\ (= t),\ \ (a,\ b,\ c \ \neq 0)$

• 벡터와 지나는 한 점이 있다면 직선의 방정식이 확정

평면의 방정식: 법선벡터와 한 점

• 한 점 $P_0(x_0,\ y_0,\ z_0)$를 지나고 영벡터가 아닌 벡터 $\mathrm{n} = (a,\ b,\ c)$에 수직인 벡터들이 이루는 평면
• 이 평면이 나타내는 것은 아래 식을 만족하는 점 $P(x,\ y,\ z)$의 집합 ($\overrightarrow{OP} = \mathrm{p},\ \overrightarrow{OP}_0 = \mathrm{p}_0$)
  $\mathrm{n} \cdot \overrightarrow{P_0P} = (a,\ b,\ c) \cdot (x - x_0,\ y - y_0,\ z - z_0) = 0$
• 이를 평면의 point-normal 방정식이라고 하고, 아래와 같이 간소화 가능
  $ax + by + cz = d\ \ \ \ \ (d = ax_0 + by_0 + cz_0)$
• 벡터방정식(평면과, 그 위의 서로 상수배가 아닌 두 벡터가 존재)
  $\mathrm{x} = \mathrm{x}_0 + t_1\mathrm{v}_1 + t_2\mathrm{v}_2,\ \ (-\infin < t_1,\ t_2 < \infin)$
• 매개방정식
  $\mathrm{x} = \mathrm{x}_0 + t_1\mathrm{v}_1 + t_2\mathrm{v}_2$
  $(x,\ y,\ z) = (x_0,\ y_0,\ z_0) + t_1(a_1,\ b_1,\ c_1) + t_2(a_2,\ b_2,\ c_2)$
• 한 점과 벡터가 주어지면 해당 벡터에 수직이면서 점을 지나는 평면이 결정
• 한 점과 두 벡터가 주어지면 평면이 결정

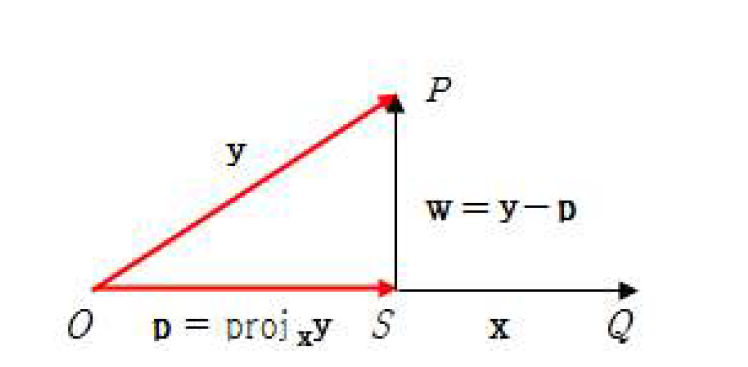
정사영

• 두 벡터 $\mathrm{x} = \overrightarrow{OQ},\ \mathrm{y} = \overrightarrow{OP}$
• 점 P에서 직선 OQ에 내린 수선의 발을 S라 하면, $\mathrm{p} = \overrightarrow{OS}$를 $\mathrm{x}$ 위로의 $\mathrm{y}$의 정사영($\mathbf{proj_xy}$)
• $\mathrm{w} = \overrightarrow{SP} = \mathrm{y} - \mathrm{p}$를 $\mathrm{x}$에 수직인 $\mathrm{y}$의 벡터성분(vector component)이라 함
  $\mathbf{proj_xy} = t\mathrm{x},\ \ \ t = {\mathrm{y} \cdot \mathrm{x} \over \mathrm{x} \cdot \mathrm{x}} = {\mathrm{y} \cdot \mathrm{x} \over ||x||^2}$

점과 평면 사이의 거리

• 점 $P_0(x_0,\ y_0,\ z_0)$와 평면 $\pi: ax + by + cz + d = 0$
• 사이의 거리
  $D = {|ax_0 + by_0 +cz_0 + d| \over \sqrt{a^2 + b^2 + c^2}}$