빅오표기법이란?

빅오 표기법은 일반적으로 시간과 공간이라는 두축을 따라서 데이터 구조나 알고리즘의 상대적 성능을 평가하는 방법이다.

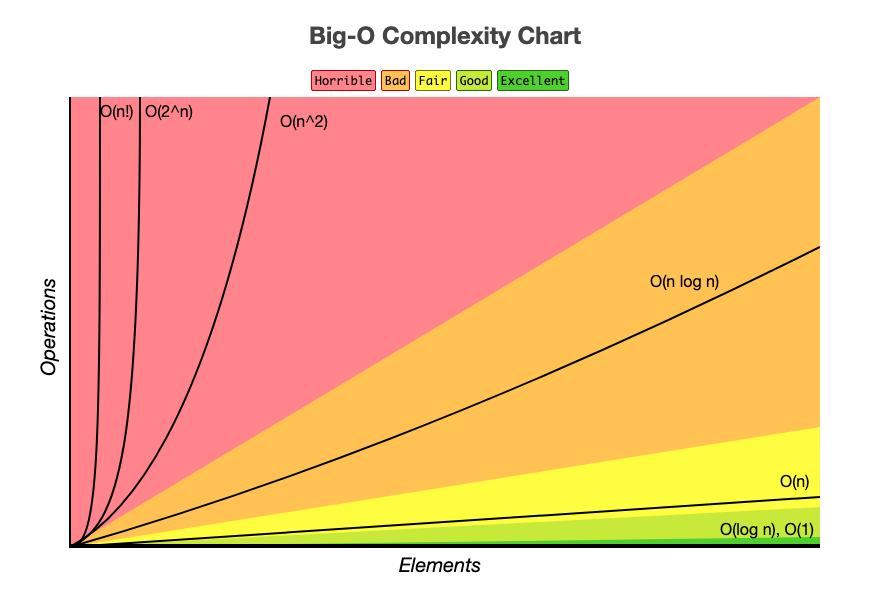
O(n)와 같이 표현해서 빅요표기법이라고 부른다!
예를 들어 Array에 존재하는 enumerated() 메서드 공식문서를 확인해보자.

이 메서드는 배열의 Index와 element를 튜플의 형태로 반환 시켜주는 메서드다.
https://developer.apple.com/documentation/swift/array/enumerated()

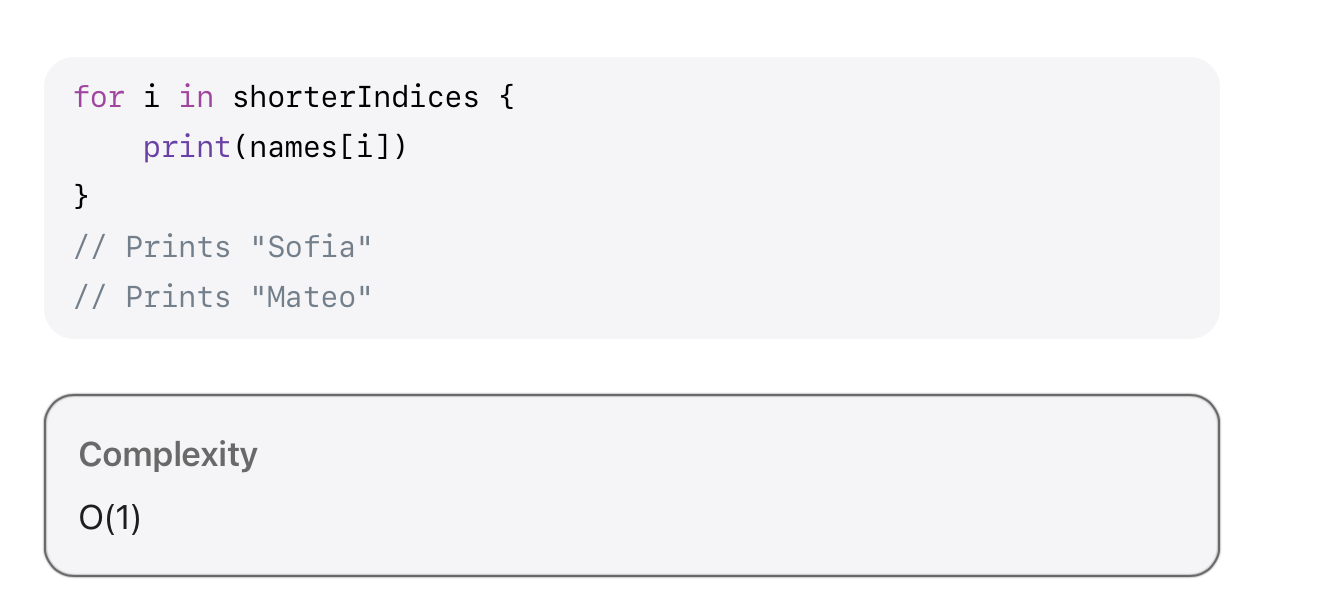
이렇게 복잡도가 적혀져 있다.
우리는 이 표기법을 확인해서 좀 더 효율적인 코드를 짤수 있다.

알고리즘에서 빅오를 결정하는 방법은 성능의 최악의 경우를 표시하는것이다. 라고 한다.

개인적으로는 이 문장이 무슨말인지 이해가 잘안간다.
그래서 우선 빅오표기법에는 어떤 종류가 있는지 확인해보겠다.

O(1) Constant Time 상수시간

func constantTime(n: Int) -> Int {
	let result = n + n
    return result
}

이와 같이 반복문이 존재하지 않고, 단순한 계산에 의해 리턴을 하는 로직을 Constant Time 상수시간이라고 부른다.
이는 굉장히 따른 작업을 한다는것이다!

O(n) 선형시간 Linear time

func linerTime(a: [Int]) -> Int {
	for i in 0..< a.count {
    	if a[i] == 0 {
        return 0
    }
    return 1
}
//어떠한 배열이 input으로 전달되면 배열 길이 만큼 요소를 검증한다.

이 경우 알고리즘 성능이 인풋값의 크기에 따라 달라진다.
배열의 길이가 1이라면 O(1) 100이면 O(100).
당연하게도 이렇게 되는경우 더이상 상수가 아니게 된다.

처리하는 데이터량이 처리하는 시간과 비례하는 경우 이것을 선형시간이라고 부른다.

만약 배열의 첫번째 요소에 0이 있는경우 물론 O(1)이다.
즉, 최적의 경우가 O(1) 이라는 말인데 위에서 이야기한대로 성능의 최악의 경우를 표시하는것이기에
O(n)이라고 표시하는 것이다.

O(log n) 로그시간Logarithmic

func logarithmic(n: Int) -> {
	var n = n
    var result = 0
    while n>1 {
   	 	n /=2 
    	result += 1
    }
    return result
}
//수를 계속 절반으로 나눠버려 금방 반복문이 끝나버린다.

이진탐색이 대표적인 O(log n) 알고리즘이다.
입력값이 2배로 증가해도 처리시간은 1만큼 증가한다.

O(n^2) Quadratic time 제곱 시간

func quadratic(_ n: Int) -> Int {
    var result = 0
    for i in 0..<n { //O(n)
        for j in i..<n { //O(n)
            result += 1
            print("\(i) \(j)")
        }
    }
    return result
}

이렇게 for문이 중첩되어 있는경우 알고리즘에 제곱시간의 효과를 줄수 있기때문에 정말 느리게 작동할수 있다고 한다.
어떠한 답을 얻기에는 문제가 없을수 있지만, 성능적으로는 좋지 않다.

공간복잡도

일반적으로 빅오 표기법에 대해서 이야기 할때는 시간복잡도에 관한것이다. 하지만 위에서 말했듯 공간 복잡도 또한 고려를 해야한다.

공간 복잡도의 경우 선언된 변수의 수와 그에 따흔 상대적 비용을 고려한다.
간단한 변수 선언의 경우 O(1)
반면에 배열이나 크기에 따라 동적으로 변하는 데이터 구조는 O(n)이 된다.

시간과 공간 교환

시간을 택할것인지 공간을 택할것인지에 대한 고민에서 시작해서 상황에 따라 적절한 코드를 작성할수 있다.

예를 들어 두개의 배열이 주어질때 공통요소가 있는지 확인하는 코드를 작성한다고 가정해보자.
일반적으로는 공통 요소가 나올때 만금 반복하게 for문을 중첩하여 이렇게 작성할수 있다.

func findCommonArray(_ A: [Int], _ B: [Int]) -> Bool {
    for i in 0..<A.count {
        for j in 0..<B.count {
            if A[i] == B[j] {
                return true
            }
        }
    }
    return false
}

이 경우 선언된 변수가 얼마 있지 않아서 공간적인 면에서 아주 효율적이지만 시간적인 면에서는 O(n^2)로 아주 비효율적이다.

반면에 시간보다 공간을 고려해야겠다고 생각한다면,
해시맵이라는 것을 구현하면 된다고 한다.

Hash Map?

해시 테이블을 기반으로 구현되는 데이터 구조이다.
Key - Value 값을 저장하고 해쉬 함수를 이용해서 데이터를 빠르게 검색 삽입 삭제할수 있다.
swift에선 Dictionary가 있다!

func arrayToHash(_ a: [Int], _ b: [Int]) -> Bool {
    
    var hashA = [Int: Bool]() //딕셔너리 타입의 선언과 동시에 초기화
    //물론 여기에 반복문이 있긴하지만 위 처럼 중첩은 아니다!
    for i in a {
        hashA[i] = true // 배열 a를 key-value로 설정해준다.
        //이렇게 저장됨 해쉬맵은 순서 보장은 안됨!
        //[2: true, 3: true, 1: true]
    }
    //hashA[3]은 true라는 유일한 value를 갖게 되는것이다.
    for j in b {
        if hashA[j] == true {
            return true
        }
    }
    return false
}

해시테이블의 경우 충돌 문제를 해결하기 위해 공간을 많이 쓴다고 한다.

하지만 코드를 보다싶이 이렇게 공간을 조금 더 차지하는 대신에 시간면에서는 유리한 결과를 얻을수 있게 됐다.
위의 경우는 시간으로써 빅오표기법의 결과는 O(n)된다.