정의와 성질
우선 트리에서 사용되는 몇가지 기본 용어를 정리해보자.
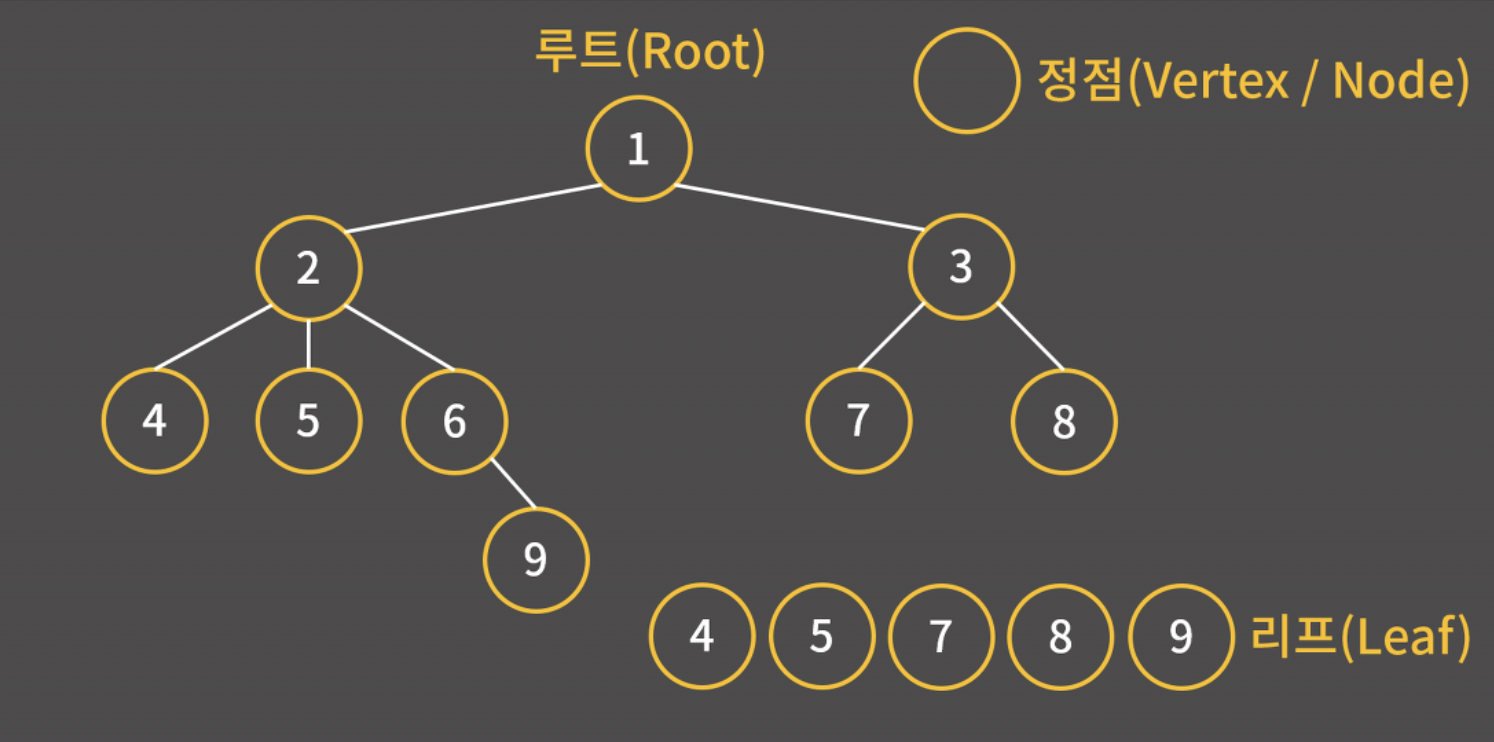
- 정점 (vertex, node): 트리의 각 원소
- 루트 (root): 트리의 제일 꼭대기에 위치한 정점
- 리프 (leaf): 트리의 제일 끝에 위치하여 자식이 없는 정점
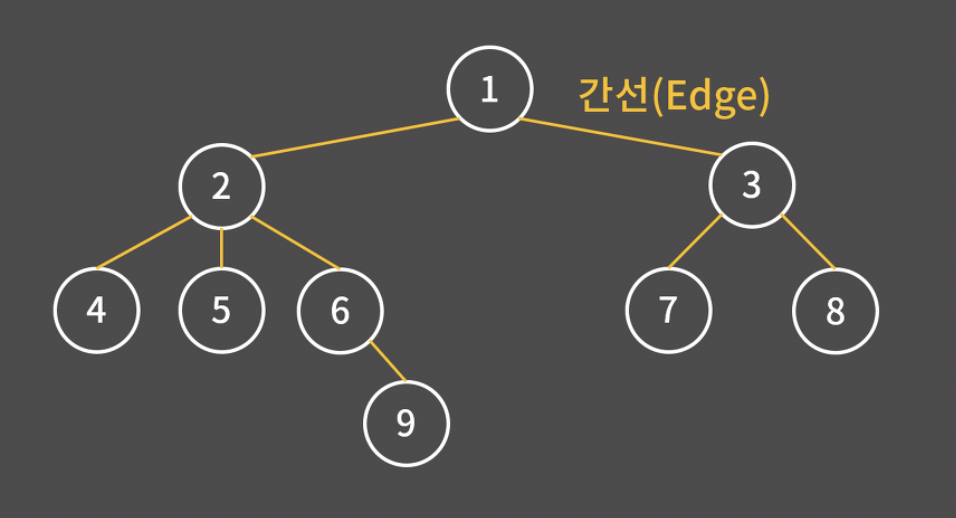
- 간선(edge): 정점을 연결하는 선
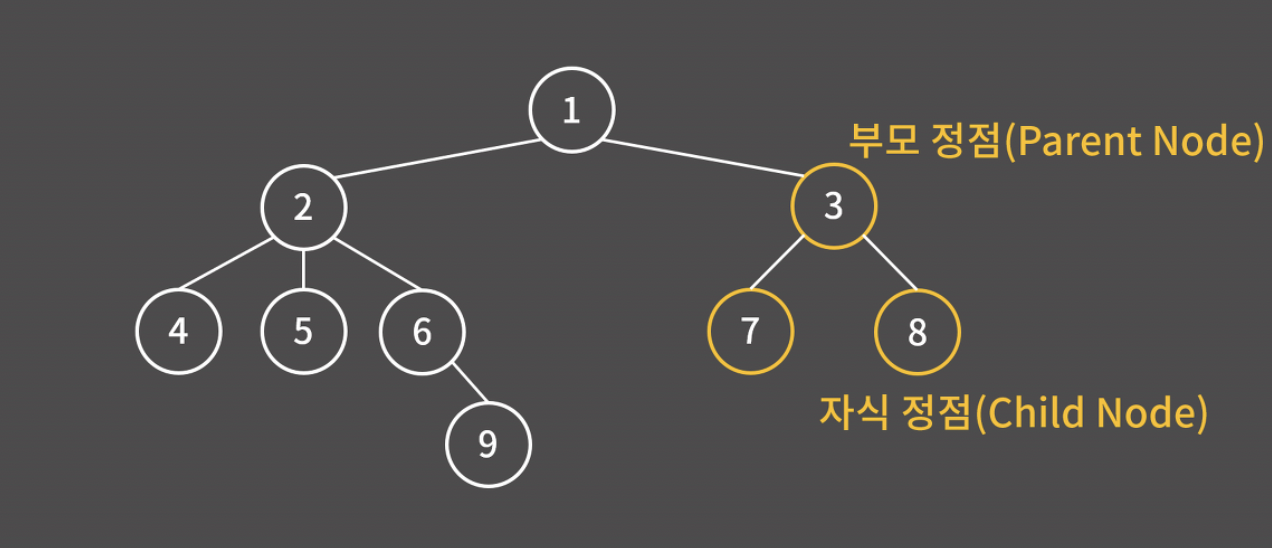
- 간선으로 연결된 위-아래의 관계를 부모-자식 관계라고 부른다. 예를 들어, 3번은 7, 8번의 부모 정점이고, 7, 8번은 3번의 자식 정점이다.
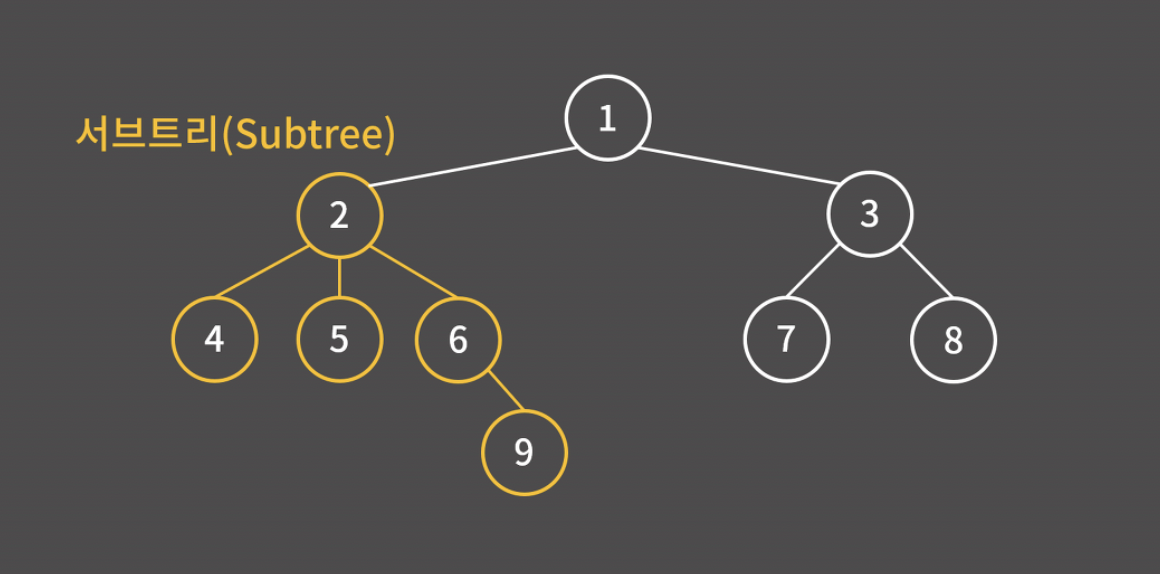
- 서브 트리(subtree): 어떤 한 정점에 대해 그 밑에 있는 정점과 간선만을 모은 트리 (주황색으로 표시한 트리는 2번 정점에 대한 서브 트리)
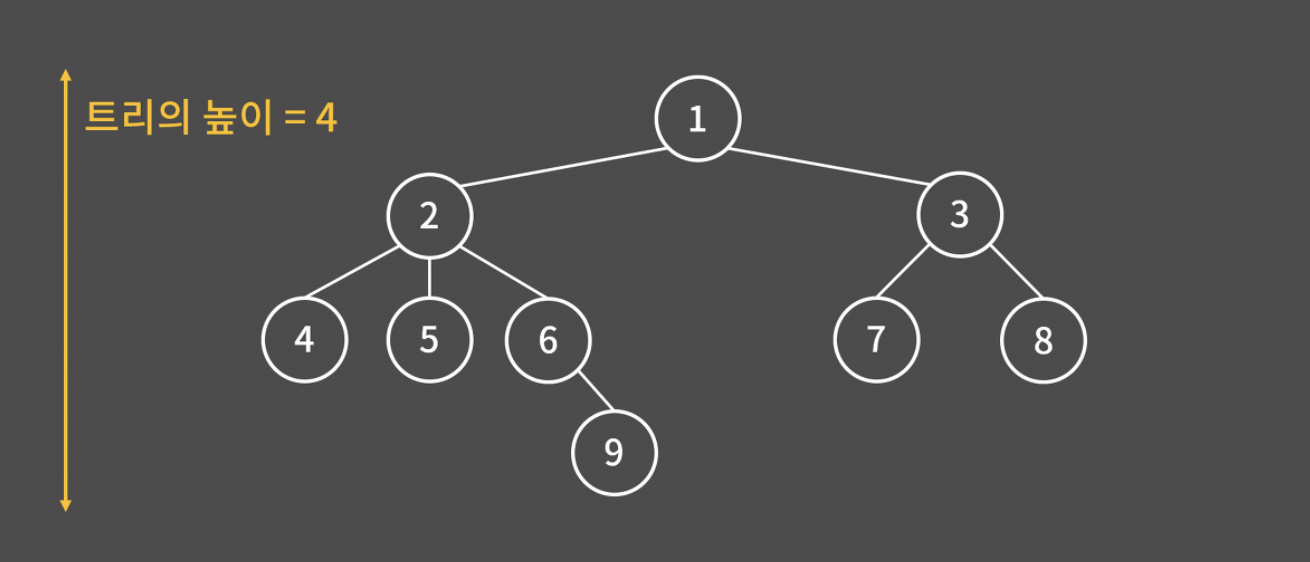
- 트리의 높이: 트리가 위아래로 뻗어있는 정도 (노드가 1개만 있을 때 높이를 1로 두느냐 0으로 두느냐에 따라서 높이가 달라짐.)
이진 트리 (Binary Tree)
이진 트리는 각 노드의 자식이 2개 이하인 트리를 말한다. 자식이 2개 이하이기 때문에 자식을 왼쪽과 오른쪽으로 구분할 수 있다.
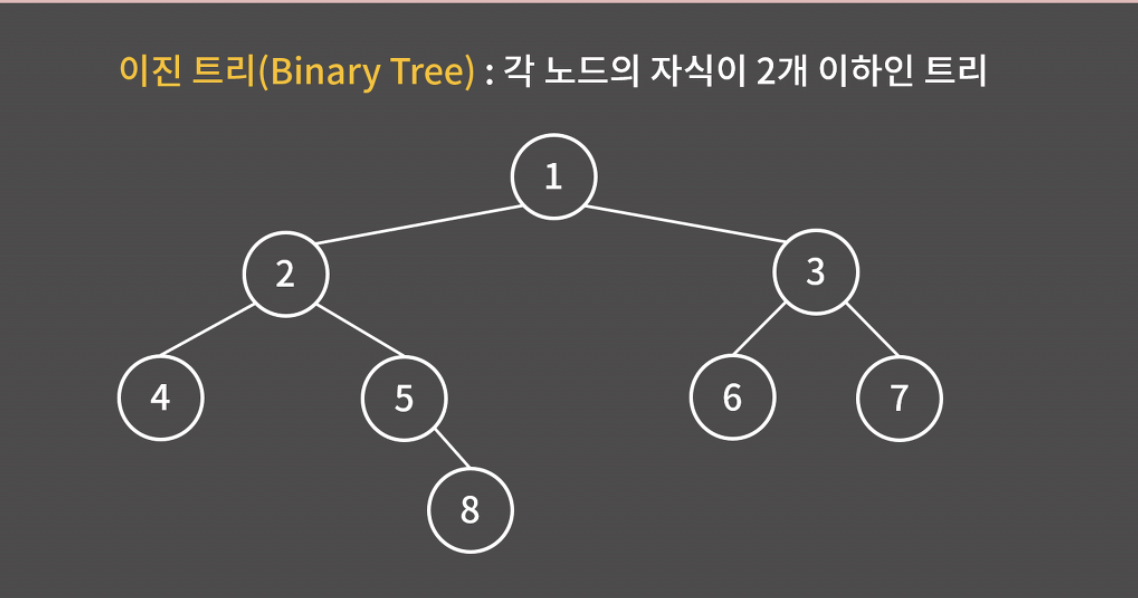
이진 검색 트리 (Binary Search Tree)
이진 검색 트리는 왼쪽 서브트리의 모든 값은 부모의 값보다 작고, 오른쪽 서브트리의 모든 값은 부모의 값보다 큰 이진 트리를 의미한다.
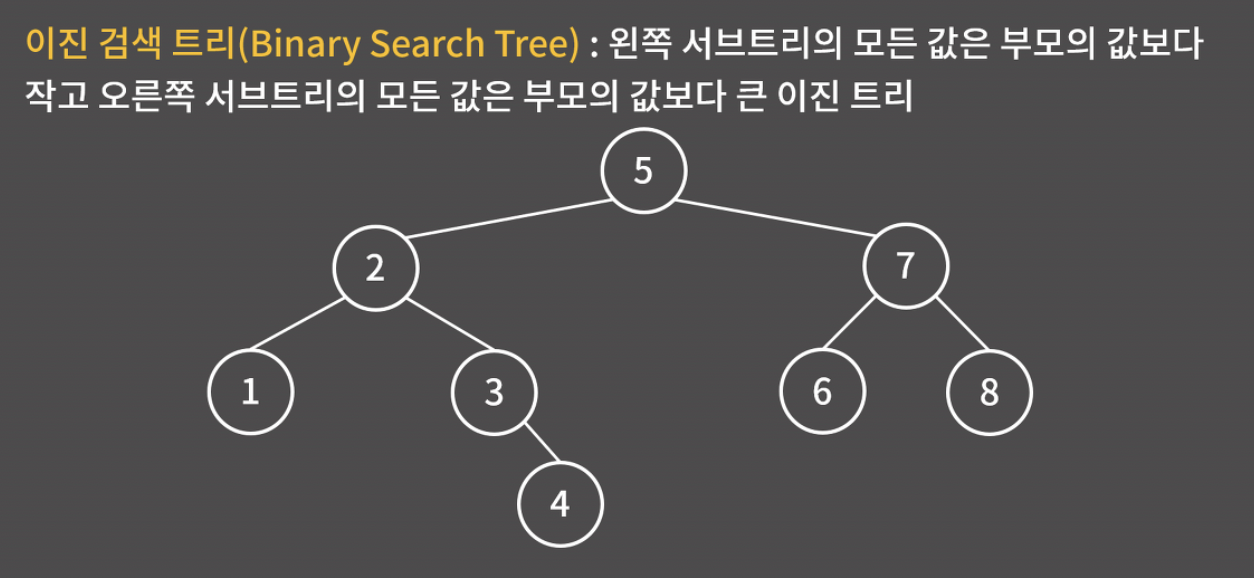
예를 들어, 루트 노드인 5번을 기준으로 왼쪽 서브트리의 모든 값 (1, 2, 3, 4)은 5보다 작고, 오른쪽 서브트리의 모든 값 (6, 7, 8)은 5보다 크다는 걸 확인할 수 있다.
🤷♀️ "그냥 배열이나 리스트에 데이터를 저장하면 되지, 왜 이진 검색 트리를 사용해야 하는가?" 에 대한 의문이 들 수 있다.
그런데, 이진 검색 트리를 사용하면 아래 연산들을 모두 O(logN)의 시간복잡도로 처리할 수 있다!
- 삽입 (insert)
- 삭제 (erase)
- 검색 및 접근 (find)
- 수정 (update)
배열에 있는 임의의 원소에 대한 검색/수정 연산은 O(1)이지만, 삽입/삭제 연산은 O(N)이 걸린다. 따라서 삽입/삭제 작업이 빈번하다면 이진 검색 트리를 활용할 수 있다.
그런데, 해시는 (비록 충돌로 인해 성능이 안 좋아질 수 있지만) 기본적으로 저 4개의 연산이 모두 O(1)이니까, 그냥 "해시가 이진 검색 트리의 상위 호환 아닌가?" 라는 생각이 들 수도 있다.
하지만, 그렇지 않다! 해시에는 없는, 이진 검색 트리의 강력한 또 다른 특성은 '원소가 크기 순으로 정렬된다'는 것이다!
예를 들어 해시에 1, 3, 5, 7, 9를 넣었는데, 여기서 '5보다 큰 최초의 원소가 무엇인지' 알고 싶다고 하자. 해시에서는 이 연산을 효율적으로 수행할 수 있는 방법이 아예 없다. 해시라는 구조 자체가 원소를 크기 순으로 저장하는 자료구조가 아니기 때문이다. 반면에, 이진 검색 트리에서는 5보다 큰 최초의 원소가 무엇인지를 O(logN)에 알아낼 수 있다.
따라서, 삽입/삭제/검색/수정 작업이 빈번하면서 동시에 원소의 대소와 관련된 성질이 필요할 때는 이진 검색 트리를 사용해야 한다.
기능
실제로 이진 검색 트리에서 삽입, 검색, 삭제를 어떻게 수행할 수 있는지 알아보자.
insert
45, 25, 35를 차례대로 삽입한다고 해보자.
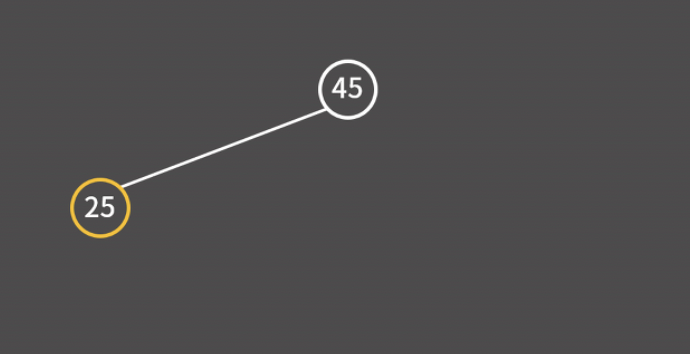
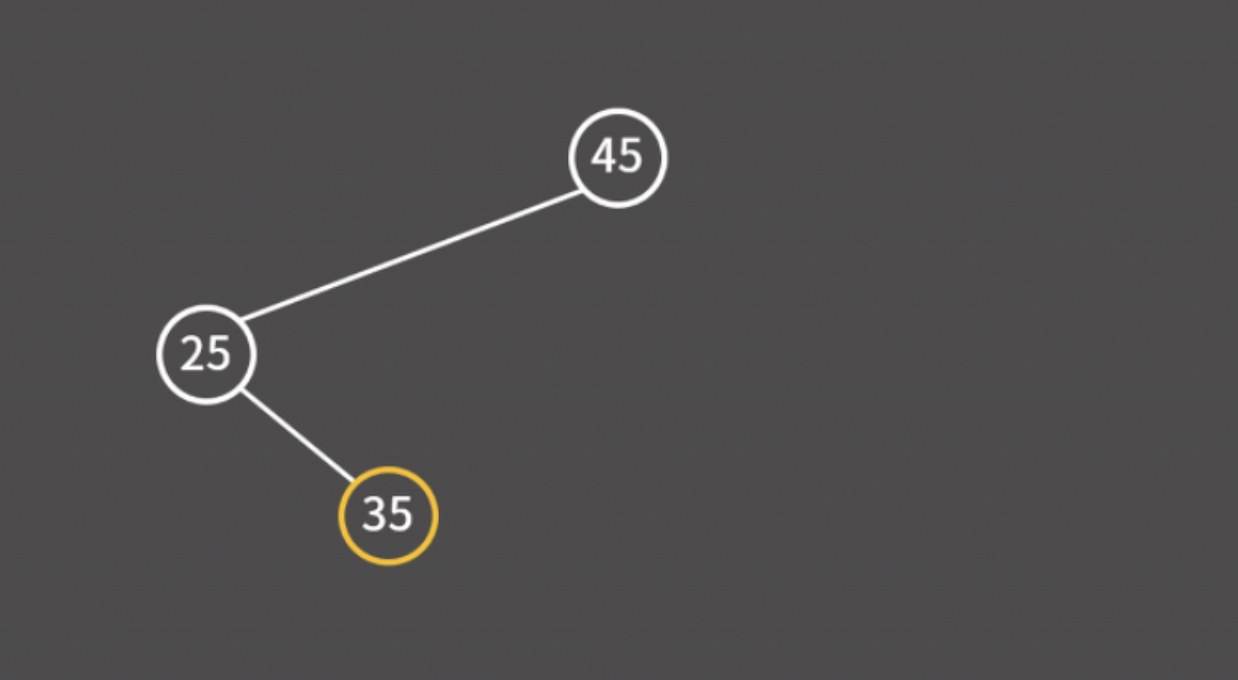
이처럼 현재 보고 있는 값과의 대소 비교를 통해 트리에서의 빈 공간을 찾을 때까지 왼쪽이나 오른쪽으로 이동하면 된다.
find
다음으로 원하는 데이터를 찾아보자. 검색도 삽입과 비슷하게 루트 노드에서 출발하여 대소 비교를 통해 좌우로 움직이면 된다.
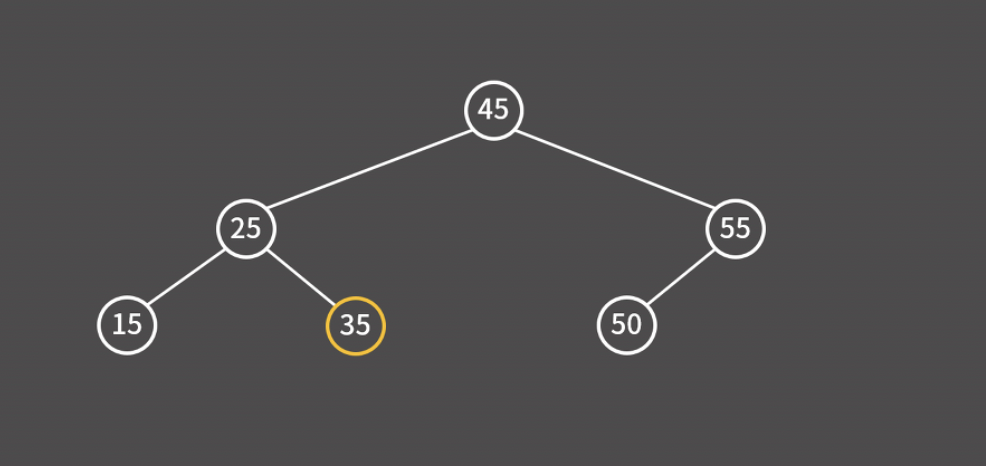
예를 들어 아래 트리 구조에서 35를 찾는다고 가정하자. 루트 노드인 45보다 작기 때문에 왼쪽으로 이동한다.
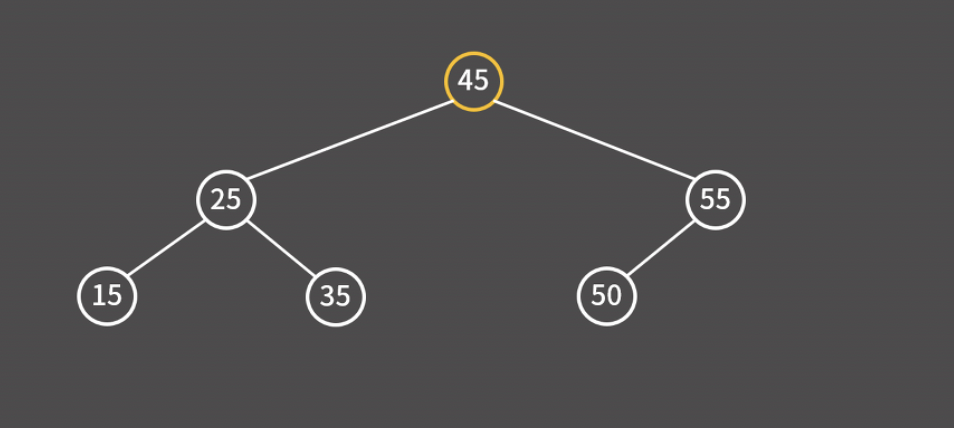
25보다 크기 때문에 오른쪽으로 이동한다.
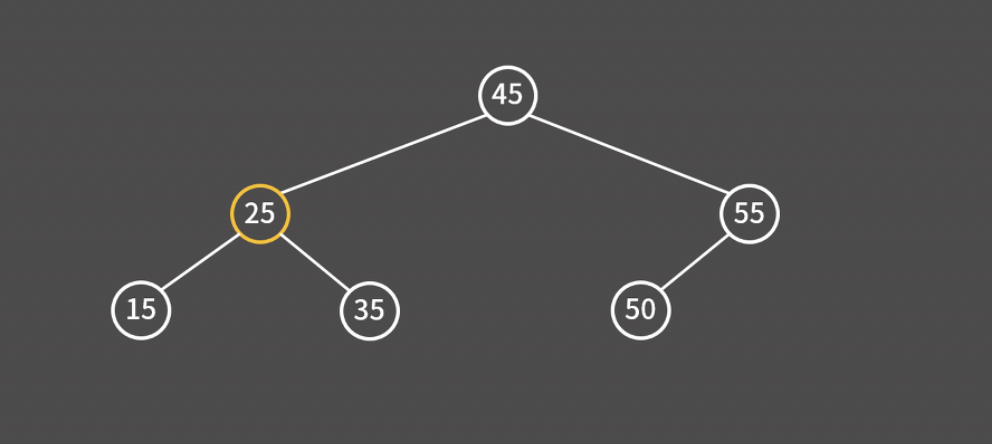
35를 찾았기 때문에 검색 과정을 종료한다.
erase
사실 이진 검색 트리에서 가장 어려운 연산은 정점의 제거이다. 아래 그림처럼 그냥 정점을 없애버리면 트리 구조가 깨지기 때문에 다른 방법을 고민해야 한다.
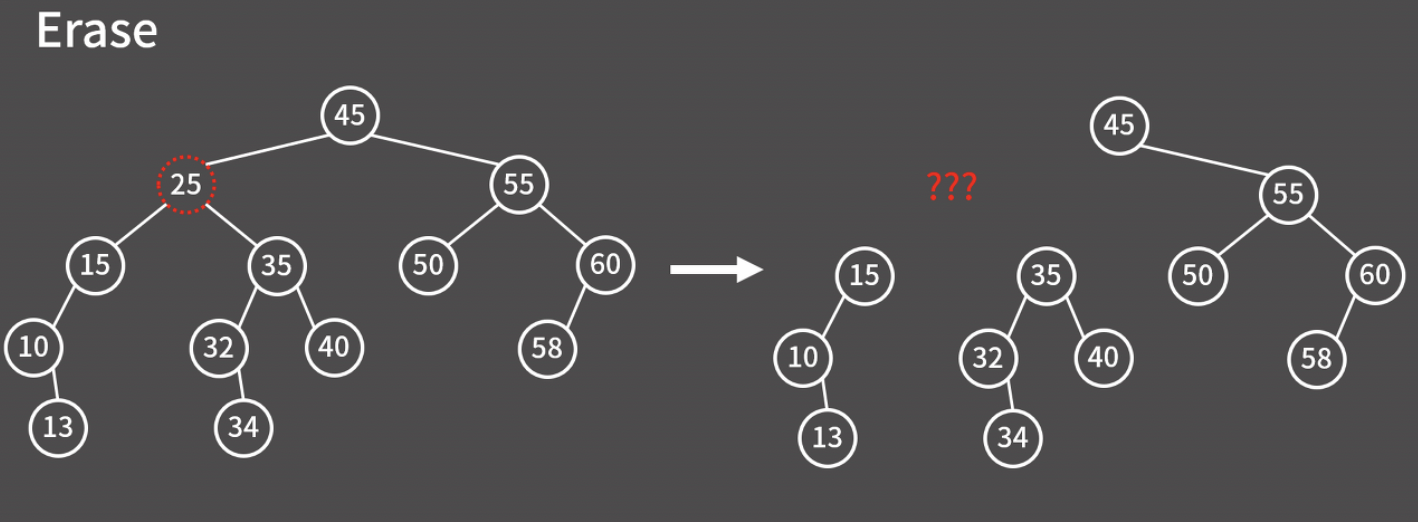
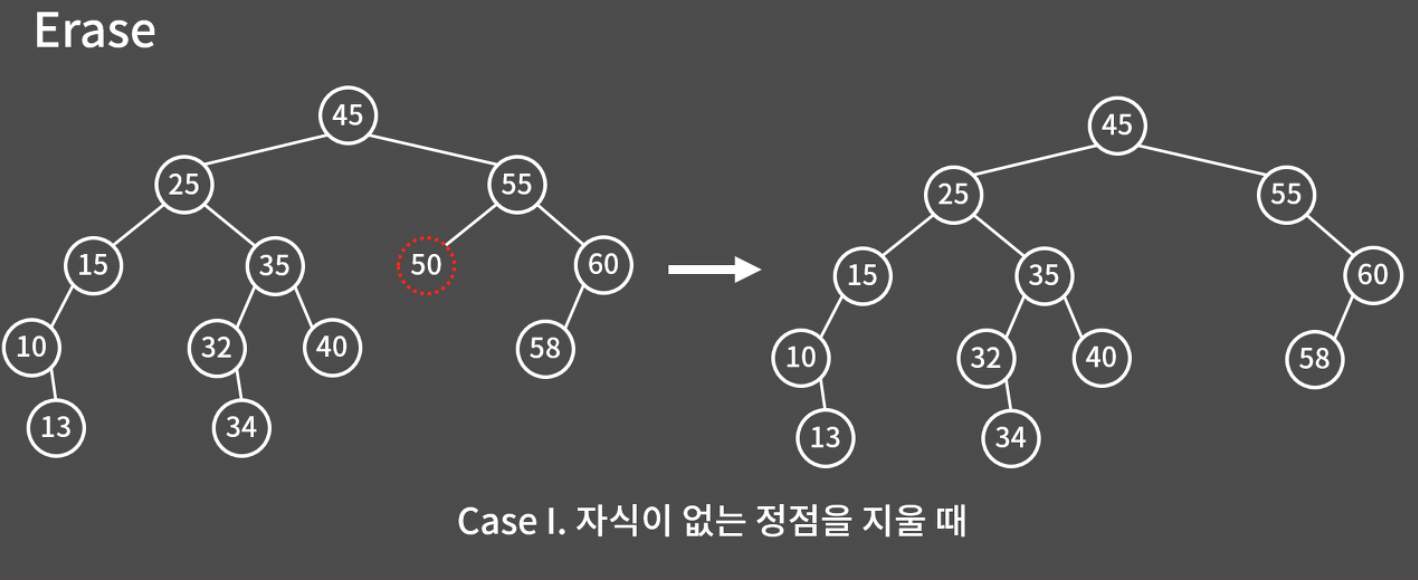
Case1. 자식이 없는 정점
이 경우에는 다행히도 정점을 그냥 삭제해도 트리 구조가 깨지지 않는다.
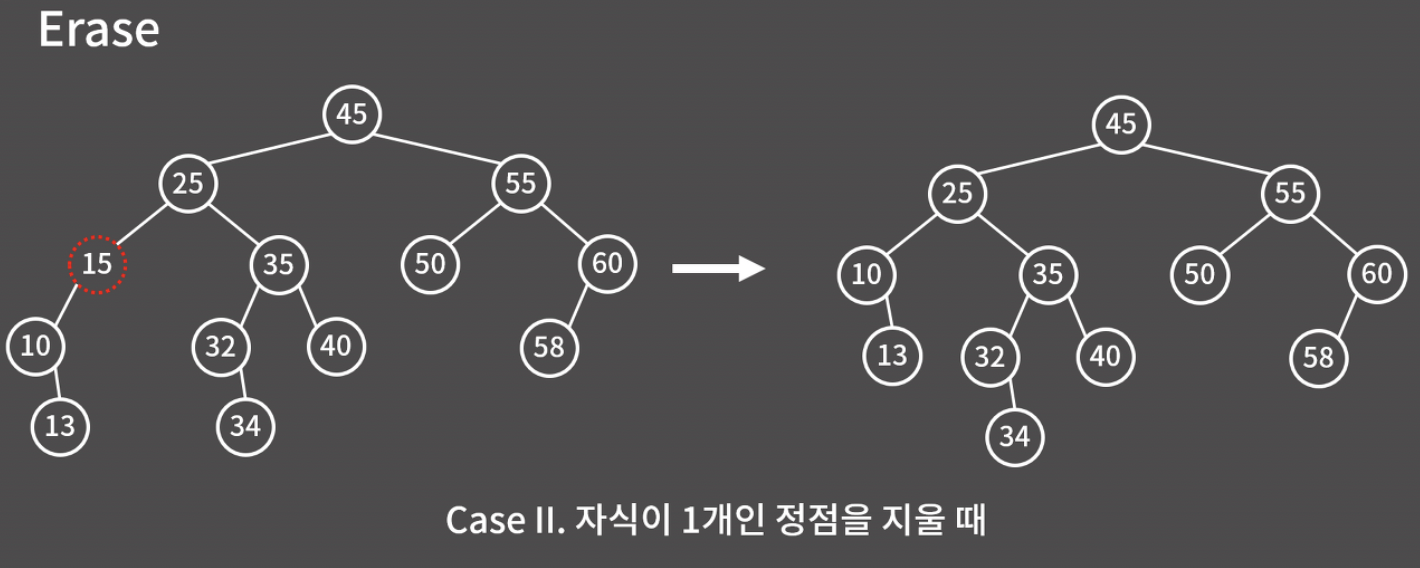
Case2. 자식이 1개인 정점
자식 노드가 1개인 정점은, 그냥 그 자식을 현재 지워진 노드의 자리로 올리면 된다.
아래 그림에서 15를 지울 때 10을 올려서, "왼쪽 서브트리의 모든 값은 부모의 값보다 작고, 오른쪽 서브트리의 모든 값은 부모의 값보다 큰" 이진 검색 트리의 조건을 잘 만족시키도록 했다.
Case3. 자식이 2개인 정점
이 경우가 가장 골치가 아픈데, 이전 방식과 비슷하게 25의 자식인 15와 35를 모두 45에 달아버리면 45의 자식이 3개가 되므로 이렇게 할 수는 없다.
비효율적인 방법으로는 그냥 25 밑에 있는 10, 13, 15, 32, 34, 35, 40을 모두 지웠다가 다시 삽입하는 방법도 있는데, 최대한 연산을 줄일 수 있는 방법을 다시 생각해보자!
가장 좋은 방법은 트리 구조를 보존할 수 있도록, 어떤 적절한 정점을 25가 있던 위치로 옮기는 것인데, 25 밑에 있는 정점들 중에서 어떤 것을 올려야 할까?
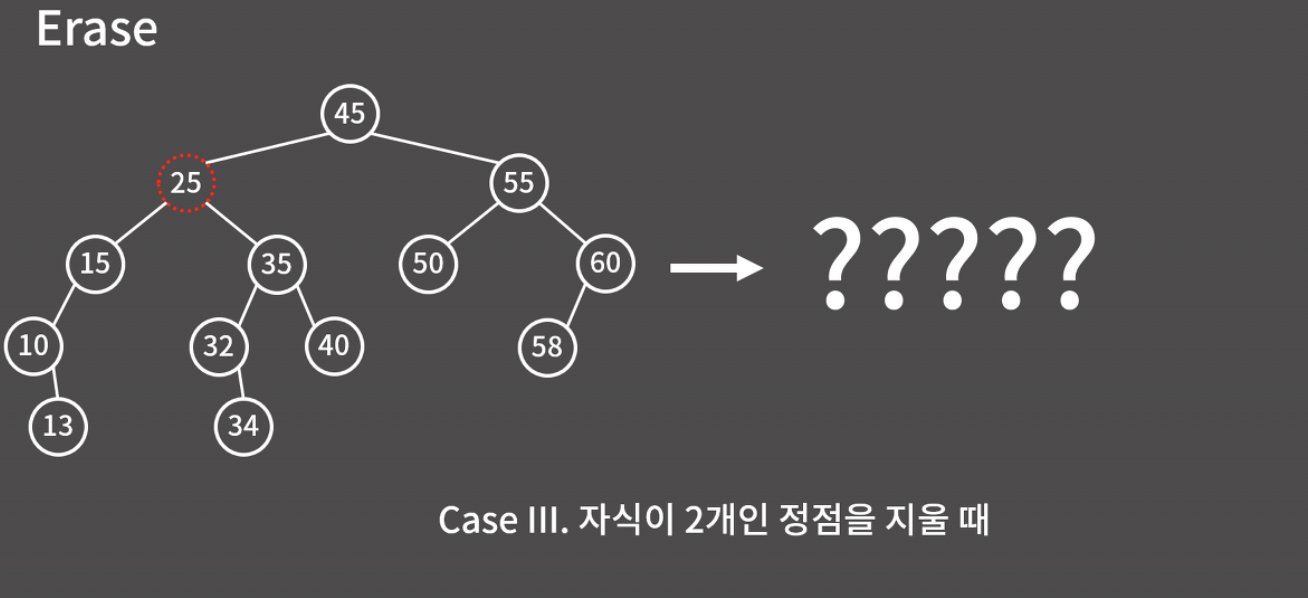
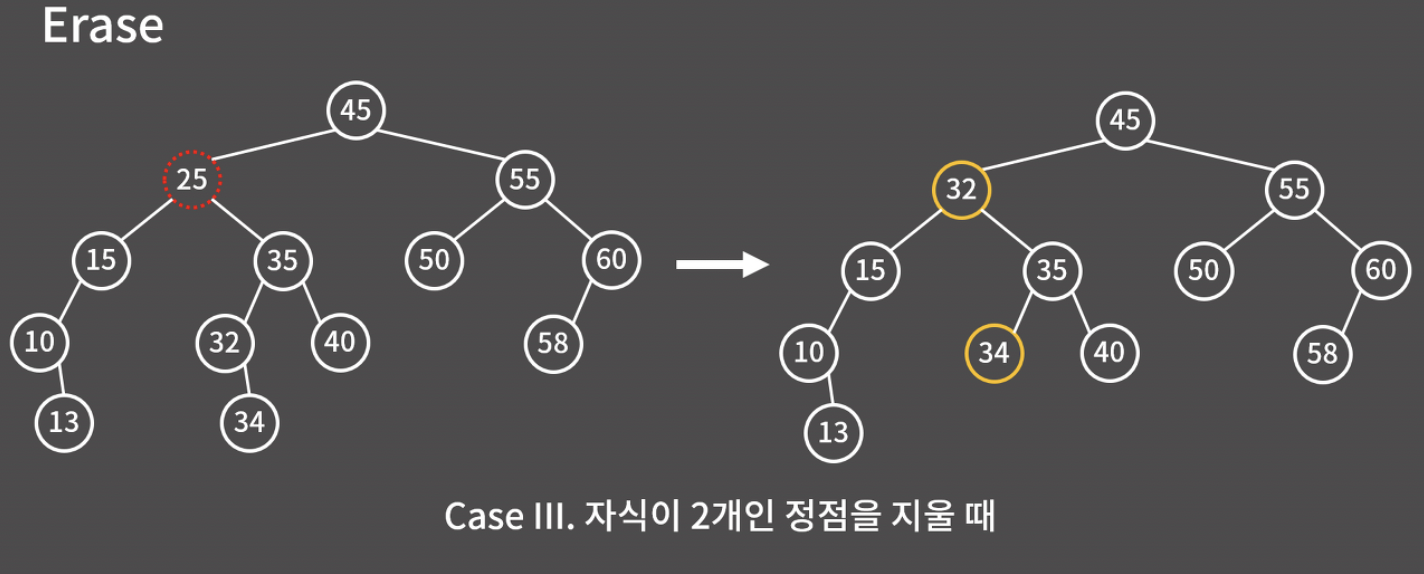
바로 '25의 오른쪽에 있는 서브트리 중에서 값이 가장 작은 노드'를 25의 자리로 올리면 된다. 아래 그림에서 32는 '25보다 크면서 가장 작은 원소'이다.
실제 구현할 때는 지우고 싶은 원소의 오른쪽 서브트리에서 계속 왼쪽으로 이동하면 된다. 그러면 '리프 노드가 현재 지우려는 원소의 값보다 크면서 가장 작은 노드'가 될 것이다.
비슷한 느낌으로 '25보다 작으면서 가장 큰' 15를 25의 자리로 올려도 된다.
그런데, 앞서 32를 지우고 25로 옮기는 게 문제 없었던 이유는 32의 자식이 하나여서 그랬다. 아래 그림처럼 32의 자식이 2개라면 어떻게 될까?
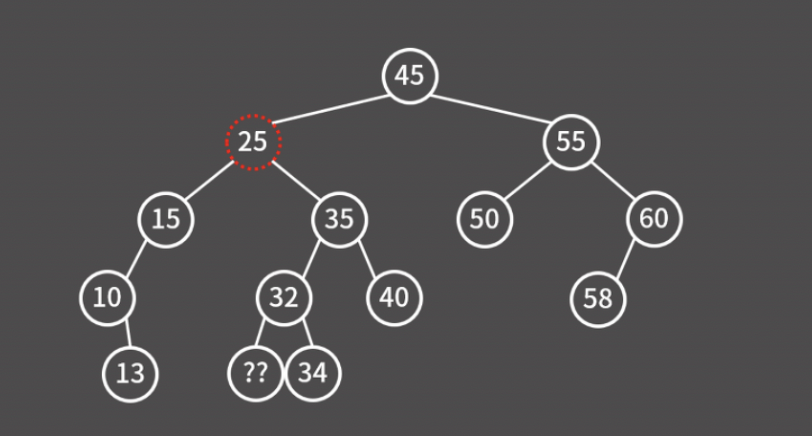
다행히 그런 일은 일어날 수가 없다. 만약 32의 왼쪽 자식 노드가 있었다면, 해당 노드야말로 25보다 크면서 가장 작은 값을 가지는 노드이기 때문이다.
마찬가지로 15의 오른쪽 자식 노드가 있었다면, 해당 노드야말로 25보다 작으면서 가장 큰 값을 가지는 노드였을 것이다.
시간복잡도
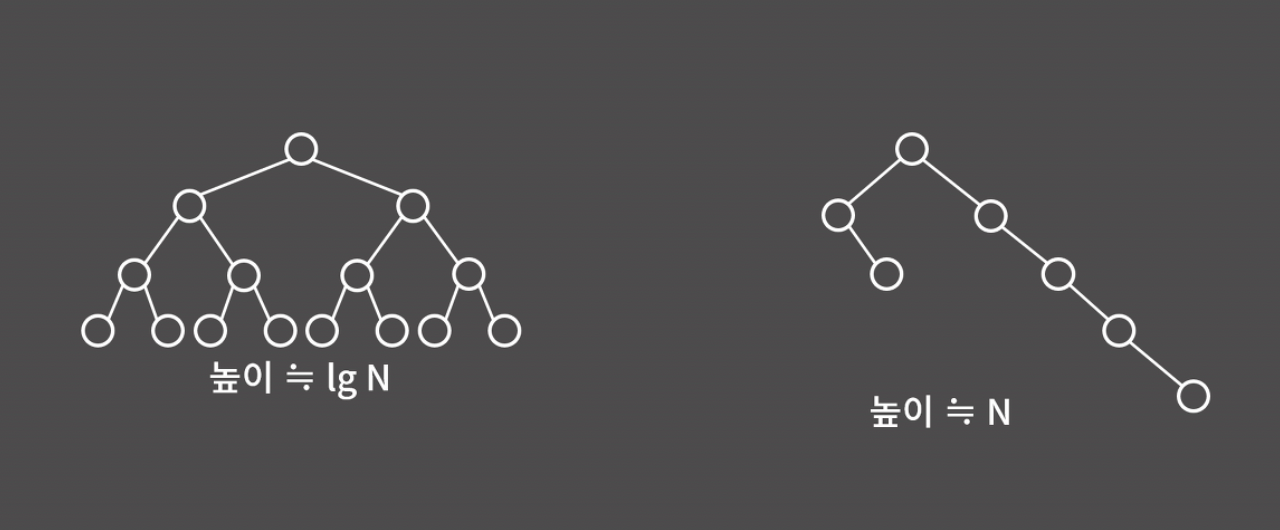
위의 세 과정은 모두 '트리의 높이가 얼마인지'에 따라 시간복잡도가 달라진다.
만약 왼쪽 그림처럼 트리의 각 정점이 대부분 2개의 자식을 가지고 있다면, 높이가 하나 내려갈 때마다 자식의 수가 1, 2, 4, 8, ... 이렇게 2배씩 증가하므로, 정점이 N개일 때 트리의 높이는 대략 logN이 된다. 이 경우 시간복잡도가 O(logN)이 된다.
반면, 오른쪽 그림처럼 트리가 편향되어있다면, 높이가 N에 가깝기 때문에 시간복잡도는 O(N)이 된다.
우리는 각 연산을 O(logN)에 수행하려고 이진 검색 트리를 쓰는 건데, 오른쪽 그림처럼 트리가 편향되어 있으면 사실상 연결 리스트에서 삽입, 삭제, 검색 연산을 하는 것과 별반 다를 게 없어진다.
트리가 편향되는 대표적인 예시는 1, 2, 3, 4, ... 이렇게 크기 순으로 주어진 원소를 삽입하는 것이며, 이런 상황은 매우 자주 발생할 수 있다.
자가 균형 트리 (Self-Balancing Tree)
따라서, 이진 검색 트리가 편향되면 이를 해결해줄 필요가 있다. 이러한 트리를 자가 균형 트리 (Self-Balancing Tree)라고 부르며, 대표적으로 AVL 트리, Red-Black 트리가 있다.
둘 중에서 AVL 트리는 구현이 조금 쉬운 편인데 성능 자체는 레드-블랙 트리가 더 좋아서, STL에 있는 이진 검색 트리는 레드-블랙 트리를 기반으로 구현되어 있다.
직관적으로 원리를 설명하자면, 아래 그림처럼 트리의 불균형이 발생했을 때 트리를 꺾어버린다고 이해할 수 있다.
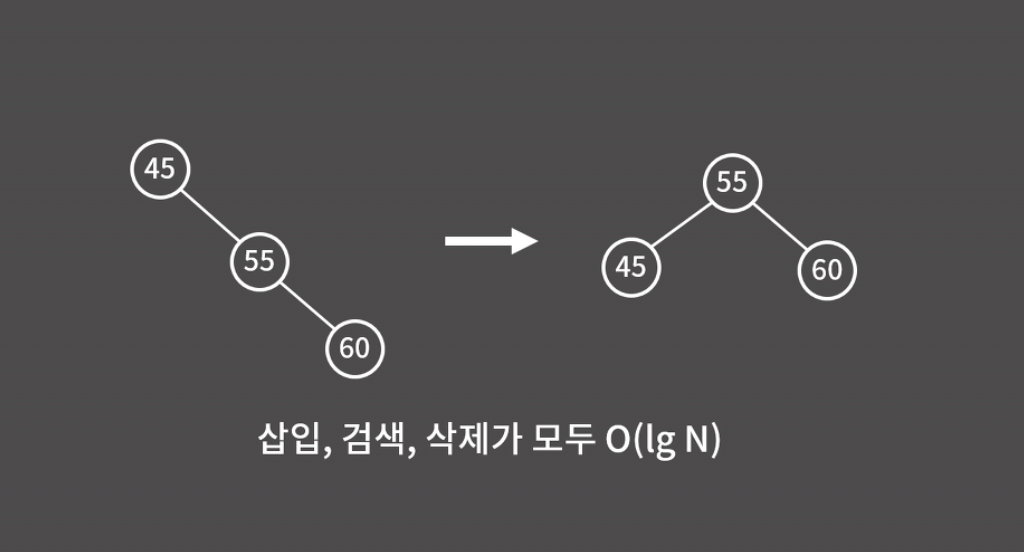
이렇게 트리의 편향성을 해소해주는 자가 균형 트리를 사용할 때, 비로소 이진 검색 트리에서 삽입, 검색, 삭제 연산 모두 O(logN)에 수행할 수 있다.
STL
이진 검색 트리는 이미 STL에 구현이 잘 되어 있고, 특히 트리의 편향 문제로 인해 직접 구현하는 게 거의 불가능에 가깝기 때문에 앞으로 이진 검색 트리가 필요할 때는 STL을 애용하면 된다.
STL에 구현된 해시는 이름이 unordered_set, unordered_multiset, unordered_map이었고, 이진 검색 트리는 이름이 set, multiset, map이다.
set
#include <iostream>
#include <set>
using namespace std;
void set_example() {
// 삽입
set<int> s;
s.insert(-10);
s.insert(100);
s.insert(15); // -10 15 100
s.insert(-10); // -10 15 100 (중복 허용 x)
// 삭제
cout << s.erase(100) << "\n"; // -10 15, 1 (삭제된 원소 개수 반환)
cout << s.erase(20) << "\n"; // -10 15, 0
// 검색
if(s.find(15) != s.end()) cout << "15 in s\n";
else cout << "15 not in s\n";
cout << s.size() << "\n"; // 2
cout << s.count(50) << "\n"; // 0
for(auto e: s) cout << e << " ";
cout << "\n";
s.insert(-40); // -40 -10 15
// -40(<-it1), -10, 15
set<int>::iterator it1 = s.begin();
// -40, -10(<-it1), 15
it1++;
auto it2 = prev(it1); // -40(<-it2), -10, 15
it2 = next(it1); // -40, -10, 15(<-it2)
advance(it2, -2); // -40(<-it2), -10, 15
auto it3 = s.lower_bound(-20); // -40, -10(<-it3), 15
auto it4 = s.find(15); // -40, -10, 15(<-it4)
cout << *it1 << "\n"; // -10
cout << *it2 << "\n"; // -40
cout << *it3 << "\n"; // -10
cout << *it4 << "\n"; // 15
}- unordered_set과 다른 점은 원소가 크기 순으로 저장되어 있다는 것
- 더 중요한 차이점은 "-40보다 크면서 가장 작은 원소가 무엇인가?"라는 문제를 풀기 위해서 unordered_set에서는 그냥 모든 원소를 다 살펴볼 수밖에 없었다. 반면, set에서는 원소가 정렬되어 있으므로 O(logN)에 찾을 수 있다.
- prev, next, advance 멤버 함수를 이용하여 좌우로 이동 가능
- begin(): 첫번째 원소의 iterator
- end(): 마지막 원소 한칸 뒤의 iterator
- size(), begin(), end(): 시간 복잡도 O(1)
- lower_bound(): 특정 원소가 삽입되어도 오름차순 순서가 유지되는 가장 왼쪽 위치
- upper_bound(): 특정 원소가 삽입되어도 오름차순 순서가 유지되는 가장 오른쪽 위치
- equal_range(): lower_bound(), upper_bound()의 쌍을 반환
- insert, erase, find, lower_bound, next, prev: 시간복잡도 O(logN)
- advance: 한칸 움직이는 게 O(logN)이므로, 여러 칸 움직이면 그에 비례하여 시간복잡도 증가
multiset
#include <iostream>
#include <set>
using namespace std;
void multiset_example() {
multiset<int> ms;
// -10 15 100
ms.insert(-10);
ms.insert(100);
ms.insert(15);
// -10 -10 15 15 100
ms.insert(-10);
ms.insert(15);
cout << ms.size() << "\n"; // 5
for(auto e: ms) cout << e << " ";
cout << "\n";
cout << ms.erase(15); // -10 -10 100, 2 (일치하는 모든 원소 삭제)
ms.erase(ms.find(-10)); // -10 100 (일치하는 한개의 원소만 삭제)
ms.insert(100); // -10 100 100
cout << ms.count(100); // 2
auto it1 = ms.begin(); // {-10(<-it1), 100, 100}
auto it2 = ms.upper_bound(100); // {-10, 100, 100} (<-it2)
auto it3 = ms.find(100); // {-10, 100(<-it3), 100}
cout << *it1 << "\n"; // -10
cout << (it2 == ms.end())<< "\n"; // true
cout << *it3 << "\n"; // 100
}- unordered_multiset과 마찬가지로 원소의 중복 허용
- erase 함수는 일치하는 모든 원소를 삭제한다는 것에 유의
- set의 find 함수는 발견된 원소의 반복자 또는 s.end()를 반환하면 되지만, multiset에서는 같은 원소가 여러 개 있을 수 있다. 이때 multiset의 find 함수는 그 중에서 아무 위치나 반환한다고 한다. (주로 첫번째 위치를 반환하는 경우가 많음.)
- 반복자가 end()를 가리키고 있는데, 이 위치의 값을 참조하려고 하면 런타임 에러가 발생한다.
- unordered_multiset과 마찬가지로 count 함수는 O(logN)이 아닌, O(원소의 개수)만큼 시간이 걸린다는 것에 유의
map
#include <iostream>
#include <map>
using namespace std;
void map_example() {
// ("bkd", 1000), ("gogo", 165), ("hi", 123) - key 기준 정렬
map<string, int> m;
m["hi"] = 123;
m["bkd"] = 1000;
m["gogo"] = 165;
cout << m.size(); // 3
// 중복 허용 x
m["hi"] = -7; // ("bkd", 1000), ("gogo", 165), ("hi", -7)
if(m.find("hi") != m.end()) cout << "hi in m\n";
else cout << "hi not in m\n";
m.erase("bkd"); // ("gogo", 165), ("hi", -7)
for(auto e: m)
cout << e.first << " " << e.second << "\n";
auto it1 = m.find("gogo");
cout << it1->first << " " << it1->second << "\n"; // gogo, 165
}- key로 value를 찾는 인터페이스가 잘 되어있는 STL
- 반복자가 가리키는 대상은 pair<string, int>이므로 it->first, it->second 이런 식으로 key, value를 가져올 수 있다.
💡 바킹독의 문제풀이 팁
문제를 풀다가 뭔가 set, map 느낌의 성질이 필요하면서 특히 lower_bound, prev, next 이런 함수를 사용해야만 풀리는 문제라면, 반드시 set, map STL을 사용해야 한다.
반면에, 그냥 key로 value를 빠르게 찾거나, 원소의 삽입/삭제/검색 연산만 빠르게 처리를 해줘야 할 때는 STL unordered_set, unordered_map을 사용해도 상관 없다.
그리고 실제로 속도를 비교해보면 평균적으로 set, map 보다 unordered_set, unordered_map 이 더 빠르다. 그럼에도 불구하고 set, map을 추천하는 이유는, unordered_set, unordered_map은 평균적으로는 빠를지언정 충돌이 얼마나 빈번하게 발생하는지에 따라 연산 속도가 저하될 수 있기 때문이다. 그래서 항상 빠르게 동작한다는 보장을 할 수 없는 치명적인 단점을 갖고 있다. 흔한 일은 아니겠지만 출제자가 의도적으로 충돌을 유발하는 데이터를 넣어둔다거나 하면, 각 연산이 O(1)이 아니라 O(N)이 되어 꼼짝없이 시간초과가 발생할 것이다.
반면 set, map은 평균적으로는 조금 느릴지언정 항상 O(logN)을 보장하는 자가 균형 트리이므로, 데이터가 어떻게 들어오든지 상관 없이 실행 시간을 예측할 수 있다.
그래서 unordered_set, unordered_map 보다는 set, map 사용을 조금 더 추천한다.
그리고 또 알아두면 좋은 것은, 이진 검색 트리의 연산은 O(logN)이지만, 같은 로그 시간 연산들에 비해서는 상당히 느리다는 점이다.
이제까지 배운 알고리즘 중에서 시간복잡도에 로그가 붙는 것은 이분탐색, 정렬 알고리즘 등이 있다.
이분탐색은 logN번의 연산 동안 인덱스의 값만 왔다갔다 이동하면 되지만, 이진 검색 트리에서는 새로운 노드를 동적할당으로 생성하거나, 트리의 편향성 해소를 위해 노드를 떼었다가 붙였다가 하는 식으로 다소 무거운 연산을 해야할 일이 많다.
따라서, 이분탐색이나 정렬에서는 N이 100만이라고 할 때, N개의 데이터에 대해서 이분탐색을 N번 하거나, 정렬을 하여 O(NlogN)짜리 연산을 수행한다고 하면, 크게 부담없이 통과되겠다고 짐작할 수 있는 반면에, 이진 검색 트리에서는 N이 100만일 때 N개의 데이터에 대해 N번 연산을 수행한다고 하면 조금 부담이 된다. 보통 시간제한이 1초라고 하면 아슬아슬하다.
따라서, 이진 검색 트리는 O(logN)이지만 조금 느리다는 걸 알아두는 게 좋다.
그리고 이진 검색 트리를 쓰는 문제인 거 같은데, N이 100만과 같이 조금 큰 상황에서 내가 생각한 풀이는 O(NlogN)인 거 같고, 시간 제한은 넉넉하지 않다면, set, map으로 풀었을 때 시간초과 날 가능성이 있다.
이럴 때는 일단 구현해보고 TLE가 난다면 STL unordered_set, unordered_map으로 교체해보고, 그래도 TLE가 난다면 set, map을 사용하지 않고, 이분탐색이나 정렬, 또는 그냥 배열의 인덱스를 갖고 푸는 문제인지 고민해볼 필요가 있다.
연습 문제
7662번. 이중 우선순위 큐
입력
- T : 테스트 케이스의 개수
- k : Q에 적용할 연산의 개수 (최대 100만)
- I n : 정수 n을 Q에 삽입
- 정수 삽입 시 값의 중복 허용
- D 1 : Q에서 최댓값 삭제
- D -1 : Q에서 최솟값 삭제
- 최댓값 또는 최솟값이 여러 개일 경우, 하나만 삭제
- Q가 비어있는데 D 연산을 적용하려고 하면 무시
출력
- 모든 연산을 처리한 뒤 Q에 남아있는 최댓값, 최솟값 출력
- 큐가 비어있으면 EMPTY 출력
이 문제는 우선순위 큐를 모르더라도 풀 수 있다.
원소 삽입, 최댓값 삭제, 최솟값 삭제를 구현해야 하는 문제인데, 그냥 배열로 구현하면 원소가 정렬되어 있지 않으므로 최댓값/최솟값을 찾는데 O(N)의 시간이 걸린다. N이 최대 k까지 커진다고 하면 총 시간 복잡도는 O(k^2)이 될 것이다. k가 최대 10^6이므로 k^2이면 10^12이어서 시간초과가 난다.
해시를 써먹을 방법이 있나 생각해봐도 해시의 특성상 해시 테이블 안에 있는 원소 중에서 최댓값/최솟값을 효율적으로 찾을 수 있는 방법이 없다.
그런데 이진 검색 트리는 딱 이 문제의 상황에 적합하다. 최솟값은 루트에서 시작하여 계속 왼쪽 자식을 타고 갔을 때 만나는 원소이고, 최댓값은 루트에서 시작하여 계속 오른쪽 자식을 타고 갔을 때 만나는 원소이다. 결과적으로 최댓값/최솟값 삭제는 O(logN)이고, 원소 삽입도 대소 비교를 하면서 트리의 좌우로 이동하면 되므로 O(logN)이다. 최종적으로는 O(klogk)의 시간복잡도가 걸린다.
이 문제는 다행히 시간제한이 6초이므로 TLE가 나지 않는다!

set, multiset, map 중에서 무엇을 사용하는 게 적합할지 고민해보자.
key, value 대응 관계가 필요 없으니 map 보다는 set, multiset이고, 원소의 중복이 허용되므로 multiset을 써야 한다.
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <queue>
#include <set>
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
int T, k;
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> T;
while(T--){
cin >> k; // 최대 100만
multiset<int> ms; // 오름차순 정렬, 중복 허용, 삽입/삭제/검색 O(logN)
for(int i = 0; i < k; i++){
char op;
int num;
cin >> op >> num;
if(op == 'I'){
ms.insert(num); // 원소의 중복 허용
}else{
// 최댓값 삭제
if(num == 1){
if(!ms.empty()) ms.erase(prev(ms.end()));
}else{
// 최솟값 삭제
if(!ms.empty()) ms.erase(ms.begin());
}
}
}
// 정답 출력
if(ms.empty()) cout << "EMPTY\n";
else {
cout << *prev(ms.end()) << " " << *ms.begin() << "\n";
}
}
return 0;
}참고로 위의 코드에서 ms.erase(*ms.begin()) 과 같이 코드를 작성하면, 일치하는 모든 원소를 삭제하는 대참사가 일어날 수 있으니 주의하자.
그리고 마지막 원소의 위치는 ms.end()가 아니라, prev(ms.end())라는 점도 주의해야 한다.

