[그리디] 다익스트라 알고리즘

leeeha·2021년 10월 19일
알고리즘
0

알고리즘

목록 보기
4/20
post-thumbnail

참고 영상: https://youtu.be/F-tkqjUiik0

최단 경로 문제

최단 경로 알고리즘은 가장 짧은 경로를 찾는 알고리즘을 의미하며, 다음과 같이 다양한 문제 상황이 주어진다.

  • 한 지점에서 다른 한 지점까지의 최단 경로
  • 한 지점에서 다른 모든 지점까지의 최단 경로
  • 모든 지점에서 다른 모든 지점까지의 최단 경로

각 지점은 그래프에서 노드로 표현하며, 지점 간 연결된 도로는 그래프에서 간선으로 표현한다.

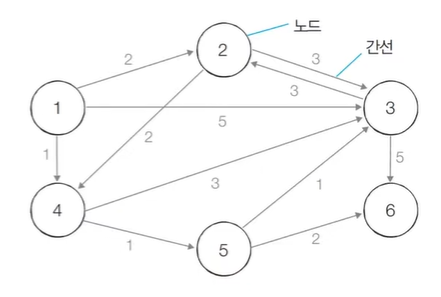
다익스트라 알고리즘 개요

  • 특정 노드에서 출발하여 다른 모든 노드로 가는 최단 경로를 계산한다.
  • 다익스트라 알고리즘은 음의 간선이 없을 때 정상적으로 동작한다.
    • 현실 세계의 도로(간선)는 음의 간선으로 표현되지 않는다.
  • 다익스트라 알고리즘은 매 상황에서 비용이 가장 적은 노드를 선택해 임의의 과정을 반복한다는 점에서 그리디 알고리즘으로 분류된다.

알고리즘의 동작 과정

  1. 출발 노드를 설정한다.
  2. 최단 거리 테이블을 초기화한다.
  3. 방문하지 않은 노드 중에서 최단 거리 테이블에 저장된 거리가 가장 짧은 노드를 선택한다. (그리디)
  4. 해당 노드를 거쳐서 다른 노드로 가는 비용을 계산해 최단 거리 테이블을 갱신한다.
  5. 위 과정에서 3번과 4번을 반복한다.
  • 알고리즘 동작 과정에서 최단 거리 테이블은 각 노드에 대한 현재까지의 최단 거리 정보를 가지고 있다.
  • 처리 과정에서 더 짧은 경로를 찾으면 '이제부터는 이 경로가 가장 짧은 경로야'라고 갱신한다.

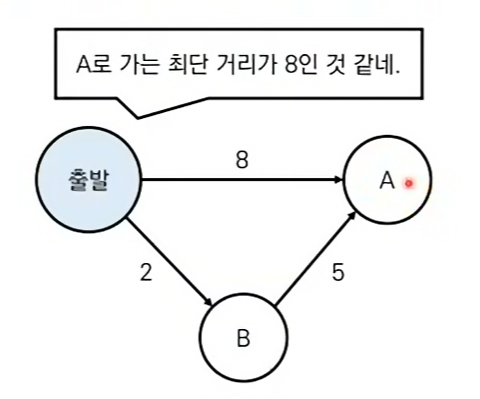
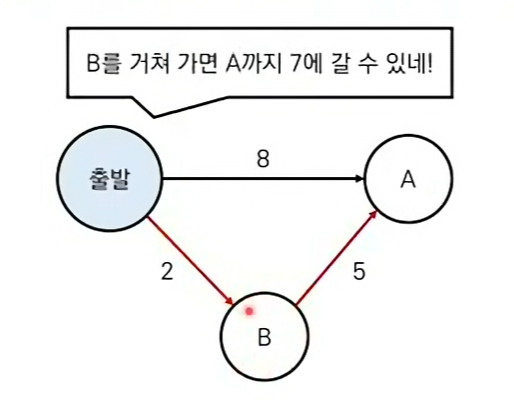
동작 과정 살펴보기

  • 그래프를 준비하고 출발 노드를 설정한다.

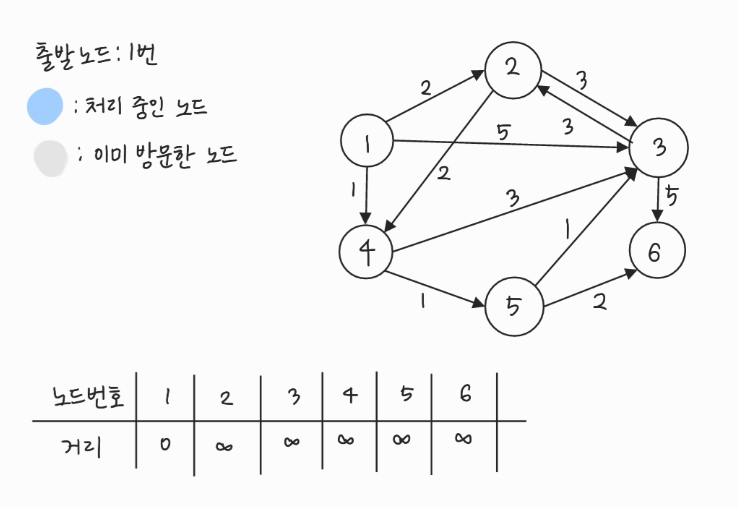
  • 방문하지 않은 노드 중에서 (최단 거리 테이블에 저장된) 거리가 가장 짧은 노드인 1번을 처리한다.
    • 1번에서 이동할 수 있는, 방문하지 않은 인접 노드: 2, 3, 4번
    • 현재 테이블에 저장된 값보다 1번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.
  • 한번 방문 처리가 된 노드는 출발 노드로부터의 최단 거리가 확정되어 테이블에 저장된 값을 변경할 수 없다. 이러한 특성 때문에 그리디 알고리즘으로 최적해를 구할 수 있다.

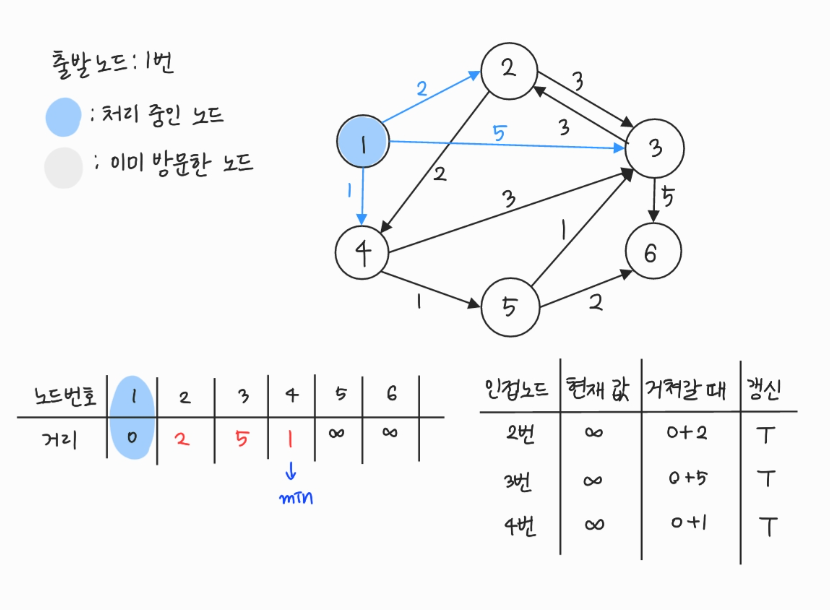
  • 방문하지 않은 노드 중에서 (최단 거리 테이블에 저장된) 거리가 가장 짧은 노드인 4번을 처리한다.
    • 4번에서 이동할 수 있는, 방문하지 않는 인접 노드: 3, 5번
    • 현재 테이블에 저장된 값보다 4번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.

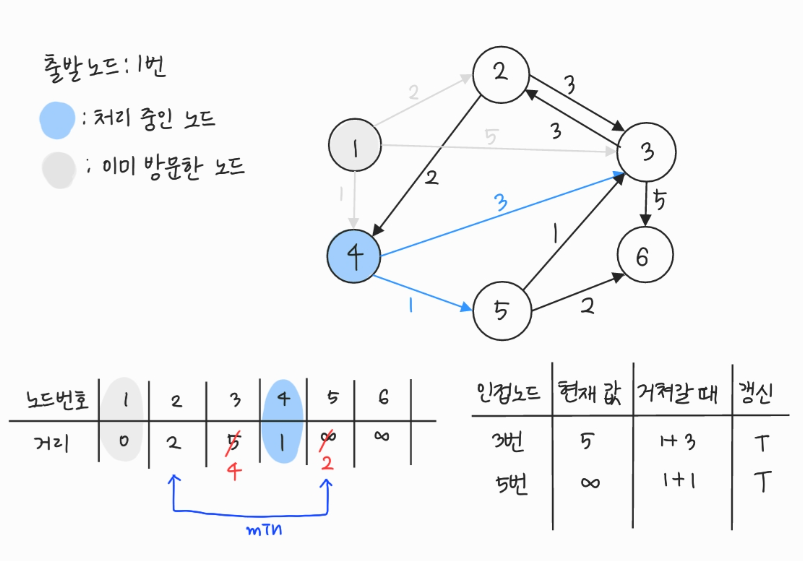
  • 방문하지 않은 노드 중에서 (최단 거리 테이블에 저장된) 거리가 가장 짧은 노드인 2번과 5번 중에 숫자가 더 작은 2번을 처리한다.
    • 2번에서 이동할 수 있는, 방문하지 않은 인접 노드: 3번
    • 4번은 방문한 적이 있기 때문에 출발 노드로부터의 최단 거리가 확정되어 값을 바꿀 수 없다.
    • 현재 테이블에 저장된 값보다 2번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.

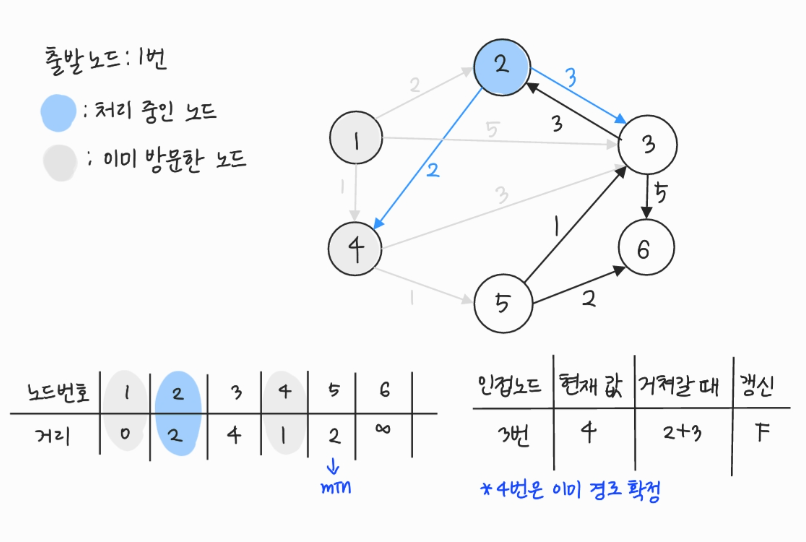
  • 방문하지 않은 노드 중에서 (최단 거리 테이블에 저장된) 거리가 가장 짧은 노드인 5번을 처리한다.
    • 5번에서 이동할 수 있는, 방문하지 않은 인접 노드: 3, 6번
    • 현재 테이블에 저장된 값보다 5번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.

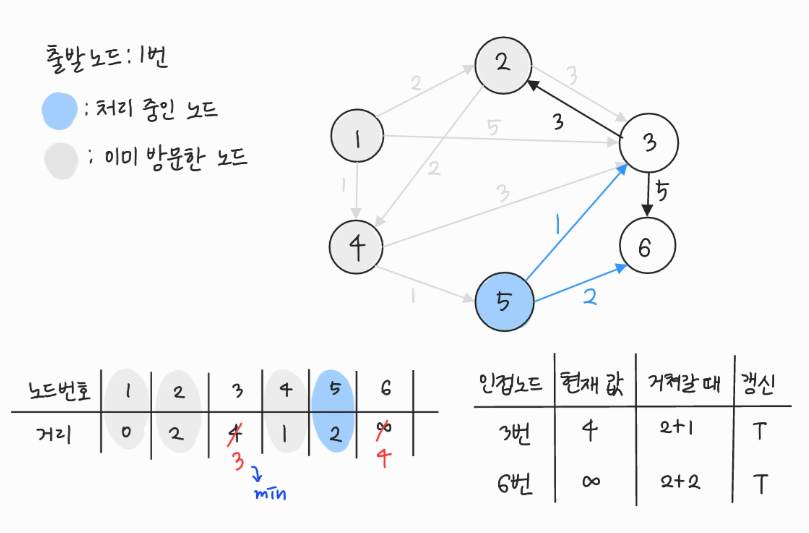
  • 방문하지 않은 노드 중에서 (최단 거리 테이블에 저장된) 거리가 가장 짧은 노드인 3번을 처리한다.
    • 3번에서 이동할 수 있는, 방문하지 않은 인접 노드: 6번
    • 현재 테이블에 저장된 값보다 3번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신한다.

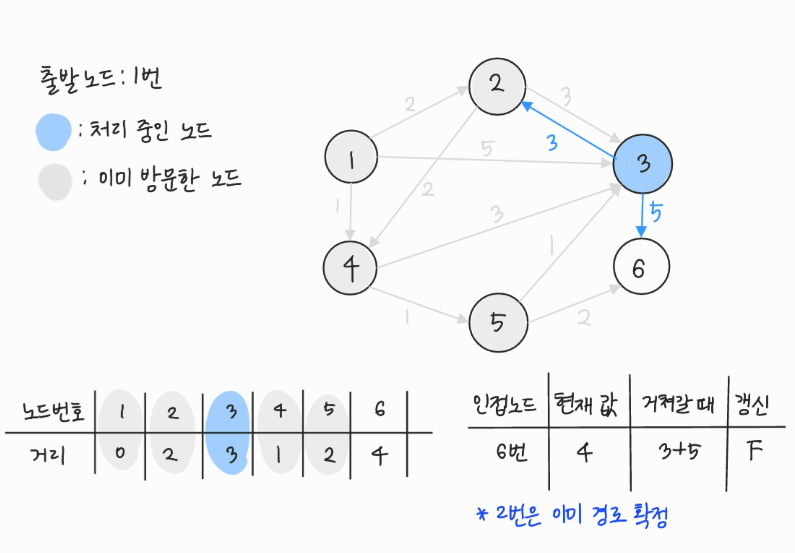
  • 방문하지 않은 노드 중에서 (최단 거리 테이블에 저장된) 거리가 가장 짧은 노드인 6번을 처리한다.
    • 6번은 이동할 수 있는 인접 노드가 존재하지 않는다.

최단경로 알고리즘_211020_021158_4

알고리즘의 특징

  • 그리디 알고리즘: 매 상황에서 방문하지 않은, 가장 비용이 적은 노드를 선택해 임의의 과정을 반복한다.
  • 단계를 거치며 한번 처리된 노드의 최단 거리는 확정되어 더 이상 바뀌지 않는다.
    • 한 단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것으로 이해할 수 있다. (따라서, 그리디 알고리즘으로 최적해를 보장할 수 있다.)
  • 다익스트라 알고리즘을 수행한 뒤, 테이블에 각 노드까지의 최단 거리 정보가 저장된다.
    • 완벽한 형태의 최단 경로를 구하려면 소스코드에 추가적인 기능을 더 넣어야 한다.

구현 방법

방법1: O(V^2)

각 단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해서 1차원 테이블의 모든 원소를 순차 탐색한다.

https://github.com/ndb796/python-for-coding-test/blob/master/9/1.cpp

#include <iostream>
#include <vector>
#define INF 1e9 
#define MAX 20001 
using namespace std;

int n, m, start;
vector<pair<int, int>> graph[MAX]; 
bool visited[MAX]; 
int d[MAX]; // 최단 거리 테이블

void input() {
	cin >> n >> m >> start;

	// 최단 거리 테이블 초기화
	fill_n(d, n + 1, INF);

	// 모든 간선 정보 입력 받기
	for (int i = 0; i < m; i++){
		int a, b, c;
		cin >> a >> b >> c;

		// a번 노드에서 b번 노드로 가는 비용이 c라는 의미
		graph[a].push_back({ b, c });
	}
}

// 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드의 번호 반환
int getSmallestNode() {
	int minVal = INF;
	int num = 0;
    
	for (int i = 1; i <= n; i++){
		if (d[i] < minVal && !visited[i]) {
			minVal = d[i];
			num = i;
		}
	}
    
	return num;
}

// 다익스트라 알고리즘 
void dijkstra() {
	// 출발 노드에 대한 초기화
	d[start] = 0;
	visited[start] = true;

	// 출발 노드에서 인접 노드까지의 거리 
    for(auto edge: graph[start]){
    	int num = edge.first; 
        int dist = edge.second; 
        d[num] = dist; 
    }

	// 출발 노드를 제외한 전체 n-1 개의 노드에 대해 반복
	for (int i = 0; i < n - 1; i++){
		// 방문하지 않은 노드 중에서
        // 최단 거리가 가장 짧은 노드에 대한 방문 처리 
		int now = getSmallestNode();
		visited[now] = true;
		
		// 현재 노드와 연결된 다른 노드 확인
        for(auto edge: graph[now]){
        	int num = edge.first; 
            int dist = edge.second; 
        	int newDist = d[now] + dist; 
            
            // 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if(d[num] > newDist) { 
            	d[num] = newDist; 
            }
        }
	}
}

void printResult() {
	// 출발 노드에서 다른 모든 노드까지 가는 최단 거리 출력
	for (int i = 1; i <= n; i++){
     	// 도달할 수 없는 경우
		if (d[i] == INF) cout << "INF" << '\n';
        // 도달할 수 있는 경우, 최단 거리 출력
		else cout << d[i] << '\n';
	}
}

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	input(); 

	dijkstra();

	printResult(); 

	return 0;
}

노드 개수를 V라고 할 때, 총 O(V)번에 걸쳐서 최단 거리가 가장 짧은 노드를 매번 선형 탐색해야 한다. 따라서 전체 시간복잡도는 O(V^2)이다.

일반적으로 코딩테스트의 최단 경로 문제에서 전체 노드의 개수가 5천개 이하라면 이 코드로 문제를 해결할 수 있다.

하지만, 노드 개수가 1만개를 넘어가는 문제라면 1초에 1억번 이상의 연산이 수행될 수 있기 때문에 시간초과가 날 가능성이 높다. 어떻게 코드를 개선해야 할까?

방법2: O(ElogV)

힙(Heap) 자료구조

참고 자료: https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

우선순위 큐는 우선순위가 가장 높은 데이터부터 먼저 삭제하는 자료구조이다.

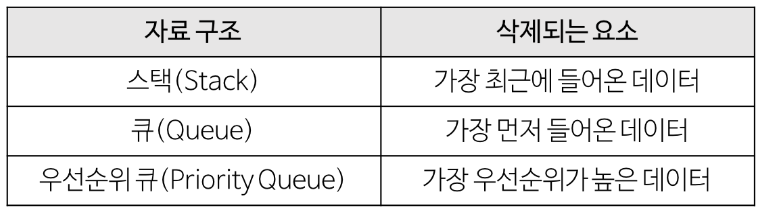
우선순위 큐는 배열, 연결리스트, 힙 등으로 구현이 가능한데, 이 중에서 힙(heap)으로 구현하는 것이 가장 효율적이다.

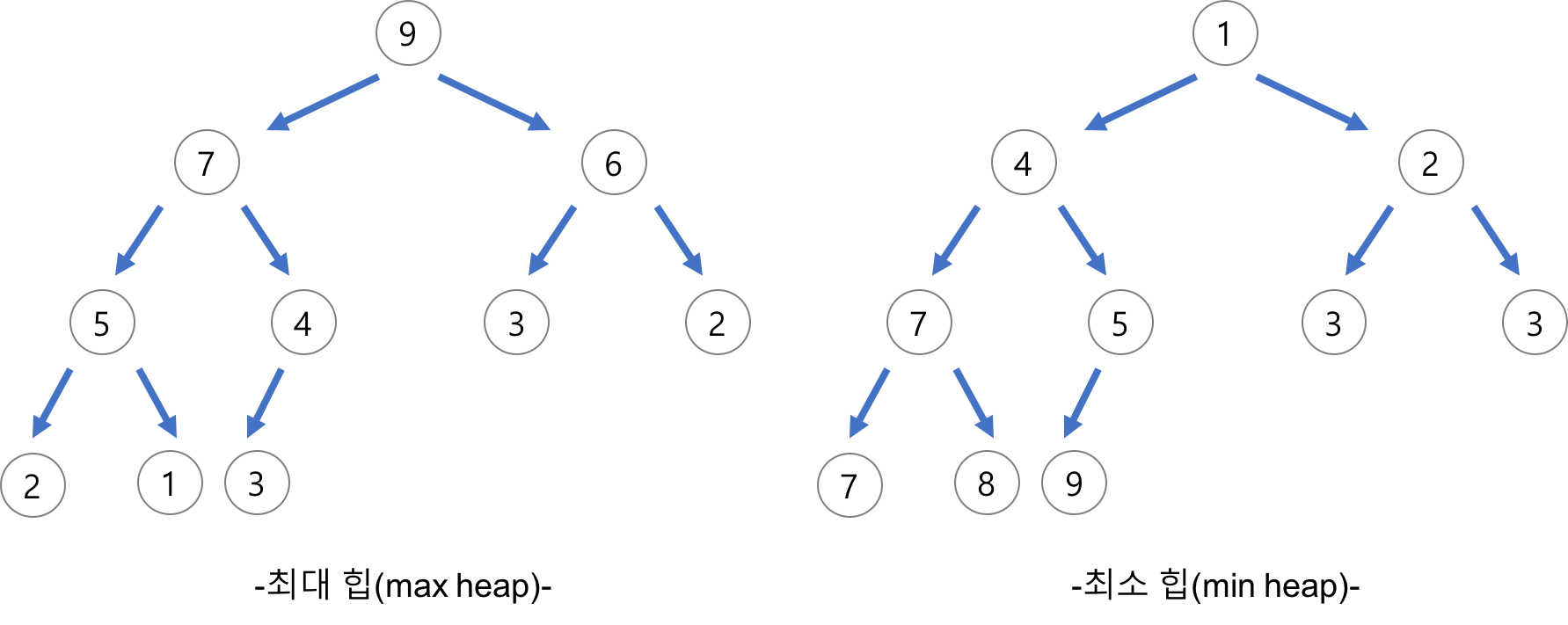
힙은 완전 이진 트리의 일종으로, 우선순위 큐를 구현하는 데 사용된다. 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾을 수 있도록 만들어진 자료구조이다.

힙은 일종의 반정렬 상태 (느슨한 정렬 상태)를 유지한다. 다시 말해, 부모 노드의 키 값이 자식 노드의 키 값보다 항상 작거나 큰 이진 트리를 유지한다. 힙에서는 중복된 값을 허용한다.

  • 최대 힙(max heap): "부모 노드의 key 값 >= 자식 노드의 key 값"을 만족하는 완전 이진 트리
  • 최소 힙(min heap): "부모 노드의 key 값 =< 자식 노드의 key 값"을 만족하는 완전 이진 트리

개선된 구현 방법

  • 단계마다 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하기 위해 최소 힙을 이용한다.
  • 다익스트라 알고리즘이 동작하는 기본 원리는 동일하다.

동작 과정 살펴보기

  • 그래프를 준비하고 출발 노드를 설정하여 우선순위 큐에 삽입한다.

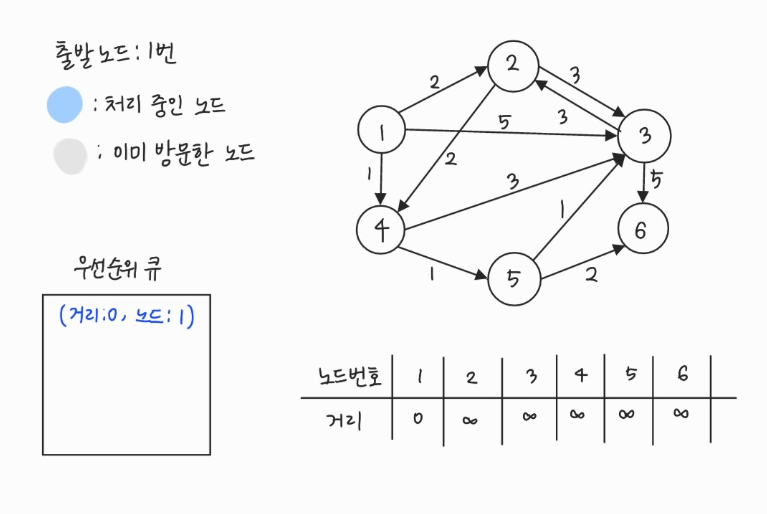
  • 우선순위 큐에서 원소를 꺼낸다. 1번은 아직 방문하지 않았으므로 방문 처리한다.
  • 1번에서 이동할 수 있는, 방문하지 않은 인접 노드: 2, 3, 4번
  • 현재 테이블에 저장된 값보다 1번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신하여 우선순위 큐에 삽입한다.

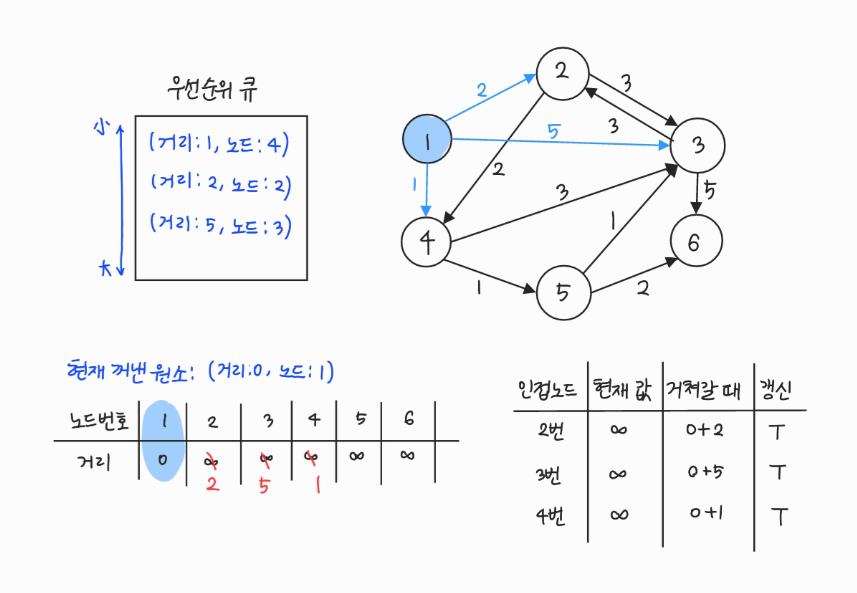
  • 우선순위 큐에서 원소를 꺼낸다. 4번은 아직 방문하지 않았으므로 방문 처리한다.
  • 4번에서 이동할 수 있는, 방문하지 않은 인접 노드: 3, 5번
  • 현재 테이블에 저장된 값보다 4번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신하여 우선순위 큐에 삽입한다.

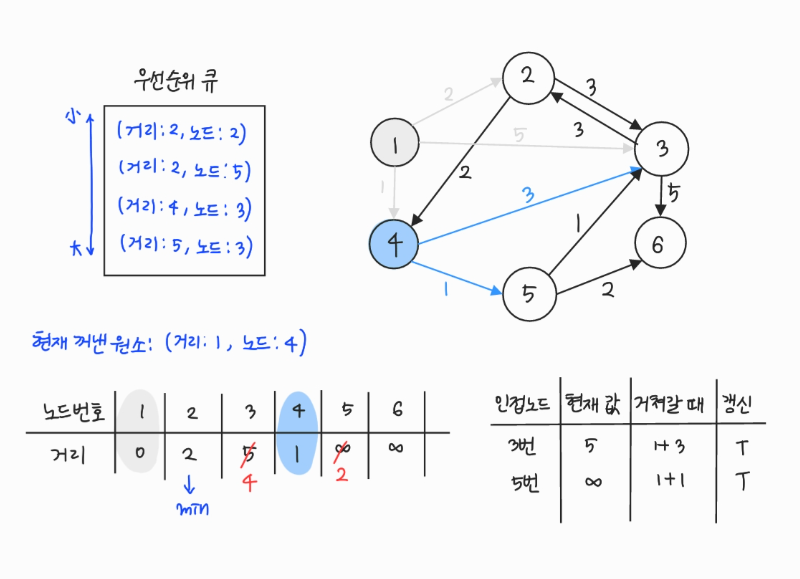
  • 우선순위 큐에서 원소를 꺼낸다. 2번은 아직 방문하지 않았으므로 방문 처리한다.
  • 2번에서 이동할 수 있는, 방문하지 않은 인접 노드: 3번
  • 현재 테이블에 저장된 값보다 2번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신하여 우선순위 큐에 삽입한다.

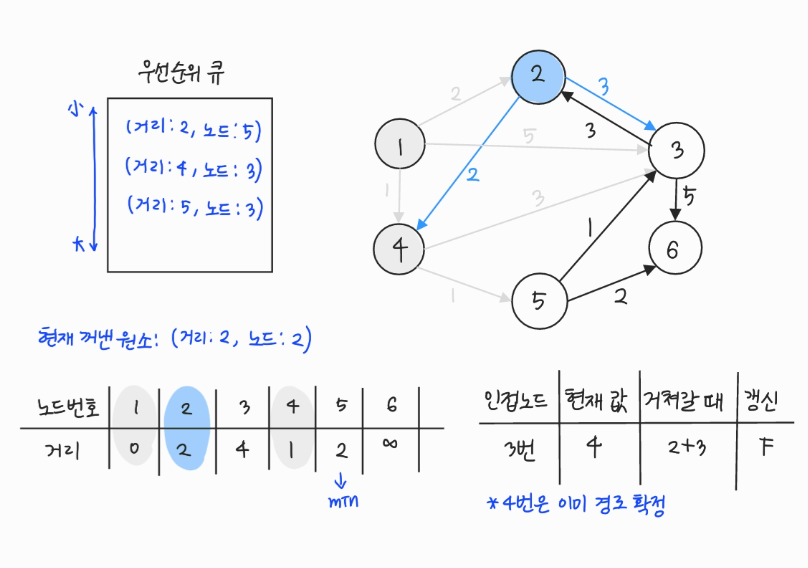
  • 우선순위 큐에서 원소를 꺼낸다. 5번은 아직 방문하지 않았으므로 방문 처리한다.
  • 5번에서 이동할 수 있는, 방문하지 않은 인접 노드: 3, 6번
  • 현재 테이블에 저장된 값보다 5번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신하여 우선순위 큐에 삽입한다.

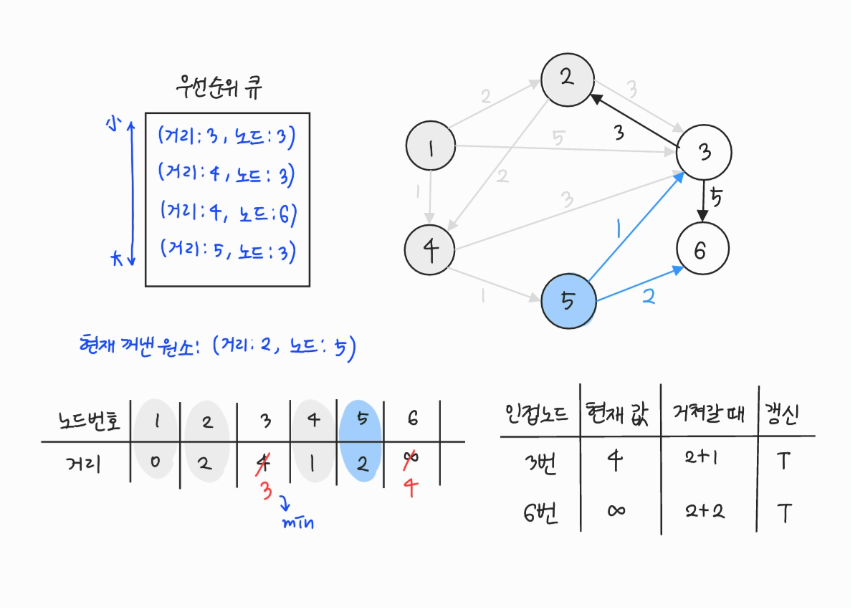
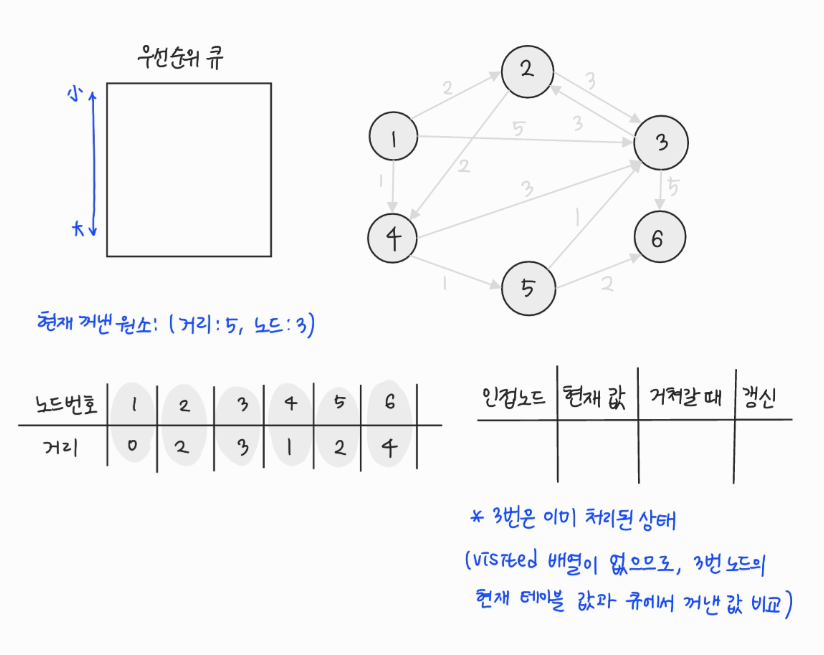
  • 우선순위 큐에서 원소를 꺼낸다. 3번은 아직 방문하지 않았으므로 방문 처리한다.
  • 3번에서 이동할 수 있는, 방문하지 않은 인접 노드: 6번
  • 현재 테이블에 저장된 값보다 3번 노드를 거쳐서 가는 경로가 더 짧으면 값을 갱신하여 우선순위 큐에 삽입한다.

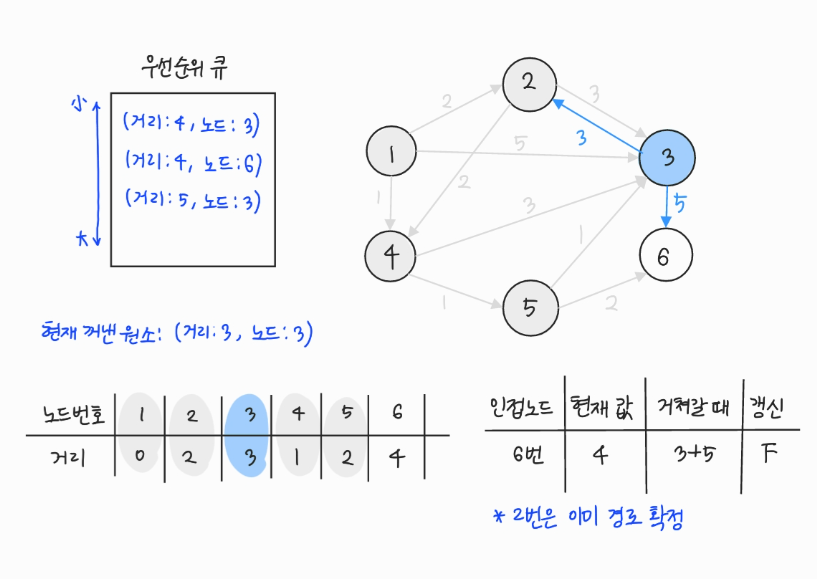
  • 우선순위 큐에서 원소를 꺼낸다. 3번은 이미 방문했으므로 무시한다.
  • 방문 여부를 저장하는 visited 배열이 없으므로, 현재 3번 노드의 최단거리 테이블에 저장된 값과 우선순위 큐에서 꺼낸 거리 값을 비교하여 방문 여부를 파악한다. (최단거리 테이블에 저장된 값이 더 작으면 방문 처리가 된 것으로 간주)

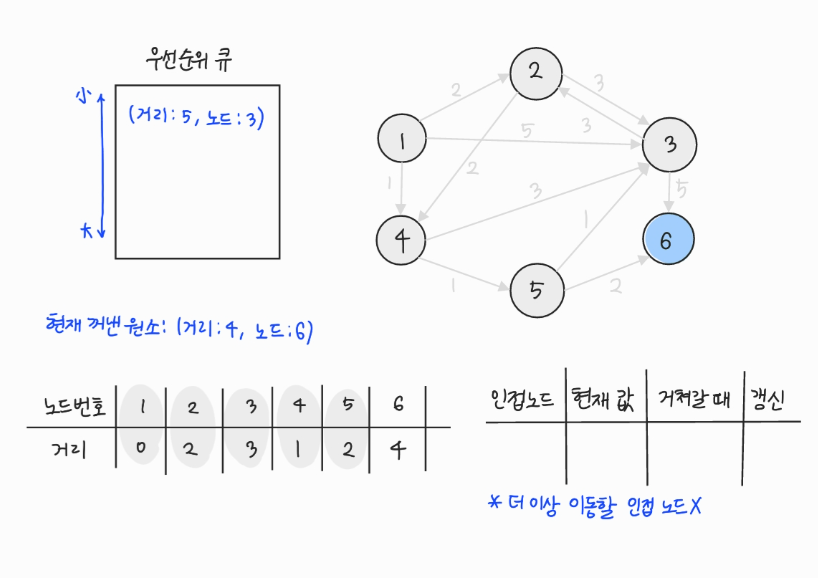
  • 우선순위 큐에서 원소를 꺼낸다. 6번은 이동할 수 있는 인접 노드가 존재하지 않는다.

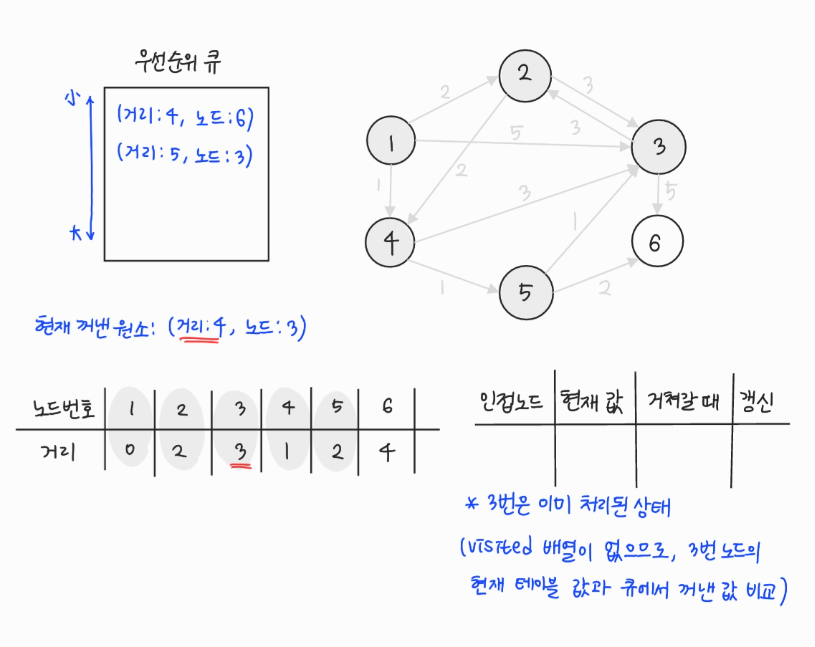
  • 우선순위 큐에서 원소를 꺼낸다. 3번은 이미 방문했으므로 무시한다.

C++ 코드

https://github.com/ndb796/python-for-coding-test/blob/master/9/2.cpp

#include <iostream>
#include <queue>
#include <vector>
#define INF 1e9
#define MAX 20001
using namespace std;

// 노드, 간선, 출발 노드 
int n, m, start;

// 각 노드에 연결되어 있는 노드에 대한 정보를 담는 배열 
vector<pair<int, int>> graph[MAX];

// 최단 거리 테이블 
int d[MAX];

void input() {
	cin >> n >> m >> start;

	// 최단 거리 테이블 초기화
    fill_n(d, n + 1, INF);

    // 모든 간선 정보 입력 받기
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;

        // a번 노드에서 b번 노드로 가는 비용이 c라는 의미
        graph[a].push_back({b, c});
    }
}

void dijkstra() {
    // 기본적으로 최대 힙으로 선언되기 때문에 
    // 거리가 가장 짧은 노드부터 먼저 꺼내는 '최소 힙'으로 구현하려면
    // 원소를 삽입, 삭제할 때 마이너스 부호를 붙여줘야 한다.
    priority_queue<pair<int, int>> pq;

    // 출발 노드에 대한 초기화
    pq.push({ 0, start }); // 거리, 노드 번호 
    d[start] = 0;

    while (!pq.empty()) {
        // 최단 거리가 가장 짧은 노드 꺼내기
        int curDist = -pq.top().first; // 출발 노드에서 현재 노드까지의 거리
        int curNum = pq.top().second; // 현재 노드 번호
        pq.pop();

        // 현재 노드가 이미 처리된 적이 있는 노드라면 무시
        if (curDist > d[curNum]) continue;

        // 현재 노드와 연결된 다른 인접 노드들을 확인
        for(auto edge: graph[curNum]) {
        	int adjNum = edge.first; 
            int cost = edge.second; 
            int newCost = curDist + cost; 
            
            // 현재 노드를 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우 
            if(d[adjNum] > newCost){
            	d[adjNum] = newCost; // 최단거리 테이블 갱신 
                pq.push({-newCost, adjNum}); // 우선순위 큐 삽입
            }
        }
    }   
}

void printResult() {
	// 출발 노드에서 다른 모든 노드까지의 최단 거리 출력 
    for (int i = 1; i <= n; i++) {
        if (d[i] == INF) // 도달할 수 없는 경우
            cout << "INF" << '\n';
        else // 도달할 수 있는 경우 거리 출력
            cout << d[i] << '\n';
    }
}

int main(void) {
	ios::sync_with_stdio(0);
    cin.tie(0);

	input(); 

    dijkstra();

	printResult(); 

    return 0;
}

(A) 우선순위 큐에서 노드를 하나씩 꺼내 검사하는 while문은 노드의 개수 V 이상으로 실행되지 않는다. 힙에서 삭제 연산은 O(logN)의 시간복잡도를 보장하므로, while문에서 걸리는 시간복잡도는 O(logV)이다.

(B) 현재 우선순위 큐에서 꺼낸 노드와 인접한 다른 노드들을 확인하는 for문은, 극단적으로 하나의 노드가 모든 다른 노드와 연결되어 있을 때 간선의 개수 E만큼 수행될 수 있다.

따라서 최종적인 시간복잡도는 O(ElogV)이다.

직관적으로, 전체 과정은 E개의 원소를 우선순위 큐에 넣었다가 모두 빼내는 연산과 매우 유사하다. 따라서 O(ElogE)의 시간복잡도로 판단할 수 있다. 그리고 중복 간선을 허용하지 않을 때 두 노드 사이에는 '오는 간선'과 '가는 간선'만 존재하므로 E < V^2이며, O(ElogE) < O(ElogV^2) < O(2ElogV) < O(ElogV) 과정을 거쳐 결과적으로 시간복잡도를 O(ElogV) 라고 판단할 수 있다.

백준 1753번 (노드 개수: 2만개)

https://www.acmicpc.net/problem/1753

노드 개수가 최대 2만개여서 첫번째 방법으로는 시간 초과가 되기 때문에, 반드시 시간복잡도가 O(ElogV)로 개선된 두번째 방법으로 구현해줘야 한다.

profile
leeeha
꾸준히!
이전 포스트

[그리디] 크루스칼, 프림 알고리즘

다음 포스트

[DP] 플로이드 워셜 알고리즘

0개의 댓글