문제

https://www.acmicpc.net/problem/11663

풀이

시간 초과: O(N^2)

#include <iostream> 
#include <vector> 
#include <string>
#include <algorithm>
#include <cstring> 
#include <queue> 
using namespace std;

vector<int> dots; 
vector<pair<int, int>> lines; 

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	int n, m; 
	cin >> n >> m; // 최대 10만 

	for(int i = 0; i < n; i++){
		int x; 
		cin >> x; 
		dots.push_back(x); 
	}

	for(int i = 0; i < m; i++){
		int a, b; 
		cin >> a >> b; 
		lines.push_back({a, b});
	}
	
	for(auto line: lines){ // 최대 10^5 
		int cnt = 0;
		int a = line.first;
		int b = line.second; 
		
		for(auto x: dots){ // 최대 10^5 
			if(x >= a && x <= b) cnt++; 
		}
		
        // [a, b] 범위에 속하는 점의 개수 출력 
		cout << cnt << endl; 
	}
	
	return 0;
}

O(N^2)으로 풀면 10^10 즉, 최대 100억번의 연산으로 시간 초과가 발생한다.

이분 탐색: O(N * logN)

• 선분의 끝점보다 큰 범위에 있는 점들 중에서 최소 좌표의 인덱스 (상한선)
• 선분의 시작점과 같거나 큰 범위에 있는 점들 중에서 최소 좌표의 인덱스 (하한선)

라고 했을 때, 선분 위에 있는 점의 개수는 상한선 - 하한선로 구할 수 있다.

그리고 C++에서 상한선은 upper_bound 함수로, 하한선은 lower_bound 함수로 구할 수 있다.

• upper_bound(first, last, value): 배열의 [first, last) 범위에서 value 보다 큰 값이 처음 등장하는 위치를 반환한다. 만약 배열의 모든 원소가 value보다 작다면, 마지막 원소 바로 다음 위치를 반환한다.
• lower_bound(first, last, value): 배열의 [first, last) 범위에서 value 이상의 값이 처음 등장하는 위치를 반환한다. 만약 배열의 모든 원소가 value보다 작다면, 마지막 원소 바로 다음 위치를 반환한다.
• 내부적으로 이분 탐색으로 구현되어 있기 때문에, 정렬된 배열에만 적용할 수 있다.

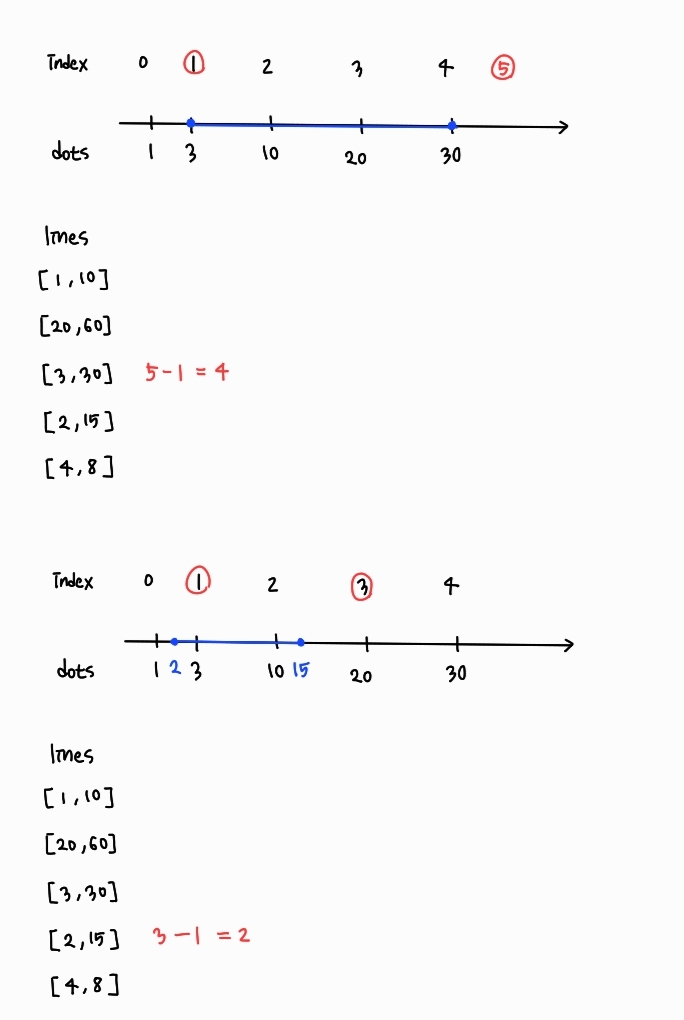
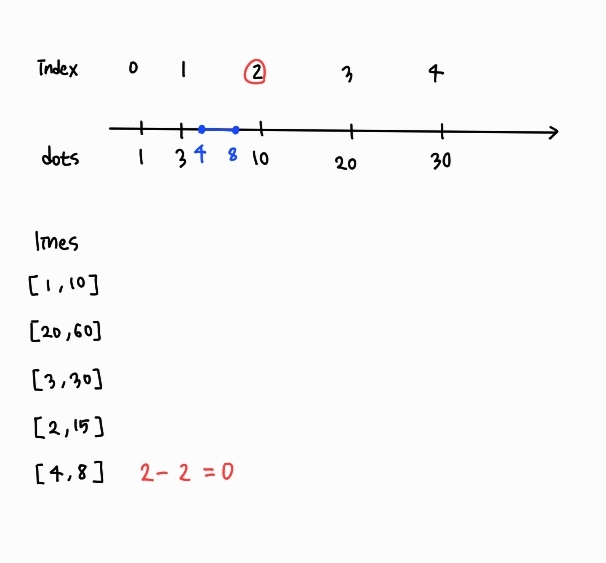
lower_bound, upper_bound 함수

이분 탐색은 정렬된 배열에 대해서만 적용할 수 있기 때문에 dots 배열을 정렬해야 한다는 걸 잊지 말자! 그리고 정답 출력 시 줄바꿈을 위해 endl을 사용하니까 시간 초과가 발생했다...

\n과 endl 모두 출력할 때 개행(줄 띄움)을 위해 사용한다. 둘의 차이는 endl은 출력 버퍼를 비워주는 과정(flush)이 들어가 있어서 \n보다 느리다.
버퍼는 입출력을 프로그램에 바로 전달하지 않고 임시 메모리 공간에 저장한 후 한번에 전송하는 역할을 한다. 버퍼를 즉시 비우고 싶다면 endl을 그렇지 않다면 \n을 사용한다.
하지만 구현체(ex. printf, println, cout 등의 출력 함수)에 따라서 "\n"도 버퍼를 비우도록 처리하는 경우도 있다고 한다.

출력 시간을 단축시키려면 \n을 사용하도록 하자!

#include <iostream> 
#include <vector>
#include <algorithm>
using namespace std;

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	int n, m;
	cin >> n >> m; // 최대 10^5

	vector<int> dots;
	for(int i = 0; i < n; i++){
		int x; 
		cin >> x; // 최대 10억 
		dots.push_back(x); 
	}

	sort(dots.begin(), dots.end()); // 정렬 잊지 말기  

	for(int i = 0; i < m; i++){ 
		int start, end;
		cin >> start >> end; 

		int ans = upper_bound(dots.begin(), dots.end(), end) - 
			lower_bound(dots.begin(), dots.end(), start);

		cout << ans << "\n"; // endl 대신 \n 사용하기 
	}
	
	return 0;
}

upper_bound, lower_bound는 이분 탐색 기반이므로 최악의 경우에도 O(logN)의 시간복잡도를 보장한다. 따라서 위의 풀이는 O(N * logN)의 시간복잡도이며, N은 최대 10^5이어서 시간 초과가 발생하지 않는다.

while문으로 직접 구현

• overIndex: 선분의 끝점인 end보다 큰 범위에 있는 점들 중에서 최소 좌표의 인덱스 (upper_bound)
• underIndex: 선분의 시작점 start와 같거나 큰 범위에 있는 점들 중에서 최소 좌표의 인덱스 (lower_bound)
• 참고: https://blog.joonas.io/153

#include <iostream> 
#include <vector>
#include <algorithm>
using namespace std;

int n, m;
vector<int> dots;

int binarySearch(int start, int end) {
	int low = 0, high = n - 1;
	int overIndex = 0, underIndex = 0;

	// upper_bound 구현 
	while(low <= high){
		int mid = (low + high) / 2;

		// end보다 크면서 최소가 되도록 
		if(dots[mid] > end){ 
			high = mid - 1;
		}else{
      		// end보다 큰 범위로 이동하도록 
			low = mid + 1; 
		}
	}

	// low, high가 교차되면 low는 end보다 크면서 최솟값 
	overIndex = low;

	low = 0, high = n - 1;

	// lower_bound 구현 
	while(low <= high){
		int mid = (low + high) / 2;

		// start와 같거나 큰 범위로 이동하도록 
		if(dots[mid] < start){
			low = mid + 1; 
		}else{
			// start 이상이면서 최소가 되도록 
			high = mid - 1; 
		}
	}

	// low, high가 교차되면 low는 start 이상이면서 최솟값 
	underIndex = low;
	
	return overIndex - underIndex; 
}

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	cin >> n >> m; // 최대 10^5
	
	for(int i = 0; i < n; i++){
		int x; 
		cin >> x; 
		dots.push_back(x); 
	}

	sort(dots.begin(), dots.end());

	for(int i = 0; i < m; i++){
		int start, end;
		cin >> start >> end;

		int ans = binarySearch(start, end);
		cout << ans << "\n";
	}
	
	return 0;
}