문제
https://www.acmicpc.net/problem/1182
풀이
참고: 순열과 조합 공식
순열 (Permutation)은 원소들 간의 순서를 고려한다. 즉, 순서가 다르면 다른 경우로 취급한다.
n개 중에 r개를 뽑고 나열하는 경우의 수는 다음과 같이 구할 수 있다.
nPr = n * (n-1) * … * (n - r + 1) = n! / (n - r)!
nPn = n!
조합 (Combination)은 순서를 고려하지 않고 그냥 뽑기만 한다. 즉, 순서가 달라도 같은 원소로 구성되어 있으면 같은 경우라고 취급한다.
n개 중에 r개를 뽑는 경우의 수는 다음과 같이 구할 수 있다.
nCr = nPr / r! = n! / (n-r)! * (r)!
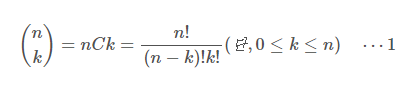
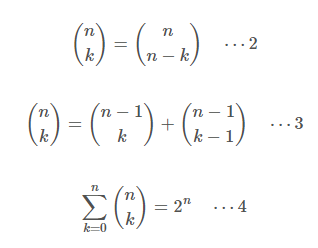
그리고 nC0 + nC1 + ... + nCn 의 경우의 수는 파스칼의 삼각형 (이항계수의 성질) 에 의해 2^n이 된다.
내 풀이
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cmath>
using namespace std;
const int MAX = 21;
int N, S;
int ans = 0;
int input[MAX];
bool selected[MAX];
int arr[MAX]; // 선택된 원소 저장
// 선택한 r개의 원소 합이 S가 되는지 검사한다.
void checkSum(int r) {
int sum = 0;
for(int i = 0; i < r; i++){
sum += arr[i];
}
if(sum == S){
ans++;
}
}
// idx - 탐색을 시작할 인덱스
// cnt - 현재까지 뽑은 개수
// r - 이번에 뽑을 최대 개수
void dfs(int idx, int cnt, int r) {
if(cnt == r){
checkSum(r);
return;
}
for(int i = idx; i < N; i++){
if(!selected[i]){
selected[i] = true;
// cnt번째로 뽑은 원소의 값 저장
arr[cnt] = input[i];
// 그 다음 경우의 수 탐색
dfs(i + 1, cnt + 1, r);
selected[i] = false;
}
}
}
int main(void) {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> S;
for(int i = 0; i < N; i++){
cin >> input[i];
}
for(int r = 1; r <= N; r++){ // O(2^N)
dfs(0, 0, r);
}
cout << ans;
return 0;
}N개 중에서 1개의 합, 2개의 합, ..., N개의 합
이 모든 경우의 수에 대해 그 합이 S가 되는지 검사하는 방법이다.
이번에 뽑을 개수 r을 1부터 N까지 증가시키며, 백트래킹으로 r개를 선택한다. (중복을 허용하지 않는 조합)
그러면 총 nC1 + nC2 + ... + nCn = 2^N - 1 이라는 경우의 수가 나온다.

실행 시간을 줄일 수 있는 다른 방법은 없을까?
다른 풀이
참고자료
N개의 각 원소에 대하여 현재 원소를 뽑을지 말지 선택하며 깊이 있게 탐색하면, 다음과 같은 이진 트리가 만들어진다.
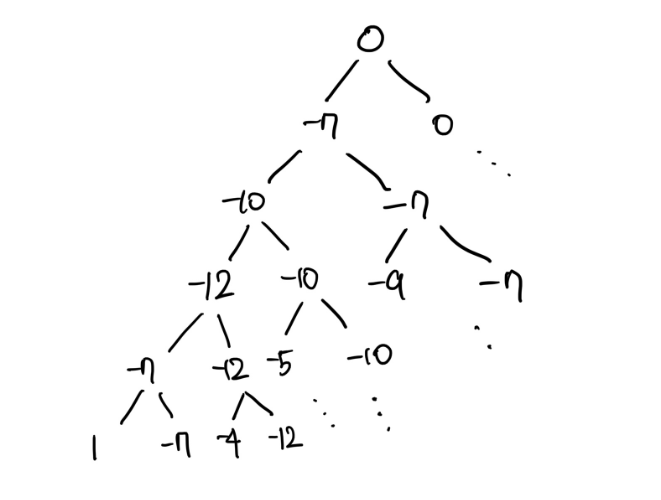
그리고 이것을 재귀호출을 이용하여 다음과 같이 구현할 수 있다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <cmath>
using namespace std;
const int MAX = 21;
int N, S;
int ans = 0;
int arr[MAX];
// idx - 선택 여부를 결정할 원소의 인덱스
// sum - 현재까지의 합
void dfs(int idx, int sum) {
if(idx == N) return; // 그 다음 경우의 수 탐색
if(sum + arr[idx] == S) ans++;
dfs(idx + 1, sum + arr[idx]); // 뽑는다.
dfs(idx + 1, sum); // 뽑지 않는다.
}
int main(void) {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> S;
for(int i = 0; i < N; i++){
cin >> arr[i];
}
dfs(0, 0);
cout << ans;
return 0;
}N개의 각 원소에 대해 뽑는다, 뽑지 않는다 라는 2가지 선택지가 있는데, 그 중에서 아무것도 뽑지 않는 공집합은 제외해야 하므로, 경우의 수는 2^N - 1이 나온다.

더 단순한 풀이를 이용하여, 시간을 엄청나게 단축시켰다!!

