문제

https://www.acmicpc.net/problem/1477

풀이

참고: https://velog.io/@rhkswls98/백준-1477-C-휴게소-세우기

기존에 휴게소 N개가 설치되어 있는 고속도로에 휴게소 M개를 더 설치한 다음

휴게소가 없는 구간 길이의 최댓값 중에 최솟값을 출력하는 문제이다.

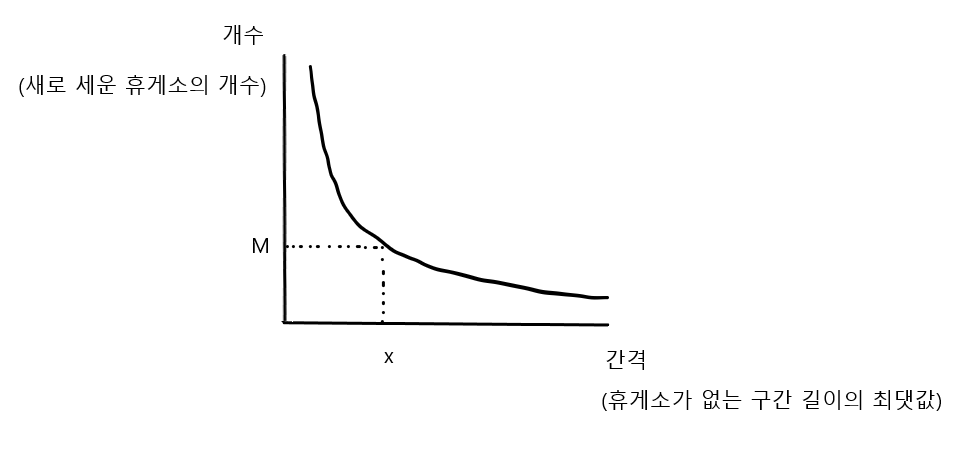
휴게소가 없는 구간 길이의 최댓값을 x라고 하면, 다음과 같은 그래프를 생각해볼 수 있다.

휴게소 간의 간격을 좁힐수록 새로 설치 가능한 휴게소 개수는 많아지고, 간격을 넓힐수록 개수는 작아진다.

우리는 "휴게소가 없는 구간 길이의 최댓값을 x라고 했을 때, 새로 설치한 휴게소 개수가 정확히 M개가 되게 하는 x의 최솟값"을 이분탐색으로 구할 수 있다.

#include <algorithm>
#include <iostream>
#include <queue>
#include <string>
#include <vector>
using namespace std;

int N, M, L; 
vector<int> arr; 

// 아직 휴게소가 세워지지 않은 구간에 
// 최대 x의 간격으로 휴게소를 세울 때, 
// 새로 세운 휴게소의 개수가 M보다 많은가? 
bool decision(int x){
	int cnt = 0; // 새로 세운 휴게소의 개수 
	
	for(int i = 1; i < arr.size(); i++){
		// 휴게소가 세워지지 않은 구간에 
		int dist = arr[i] - arr[i - 1];

		// x의 간격으로 새 휴게소를 세운다. 
		cnt += dist / x; 

		// 나눠떨어지는 경우에 대한 예외 처리 
		if(dist % x == 0) cnt--;
	}
	
	return cnt > M; 
}

int main() {
  	ios::sync_with_stdio(0);
  	cin.tie(0);

	cin >> N >> M >> L; 

	// 시작점, 끝점으로부터 휴게소까지의 거리도 구해야 하므로 벡터에 추가 
	arr.push_back(0);
	arr.push_back(L);
	
	// 기존 휴게소의 위치 입력 
	for(int i = 0; i < N; i++){
		int x; 
		cin >> x; 
		arr.push_back(x); 
	}

	// 이분탐색 전에 정렬 먼저!! 
	sort(arr.begin(), arr.end()); 

	// 휴게소 간 거리의 최솟값, 최댓값 설정 
	int left = 1; 
	int right = L; 
    
    // 휴게소가 없는 구간 길이의 최댓값 중에 최솟값 
	int ans = 1e9;  

	while(left <= right){
		int mid = (left + right) / 2; 

		// 새로 세운 휴게소가 M개보다 많으면 
		if(decision(mid)){ 
        	// 간격을 더 늘린다. 
			left = mid + 1; 
		}else{ // M개와 같거나 더 적으면 
         	// 최솟값 갱신 
			ans = min(ans, mid);
            // 간격을 줄인다. 
			right = mid - 1; 
		}
	}

	cout << ans; 
	
  	return 0;
}

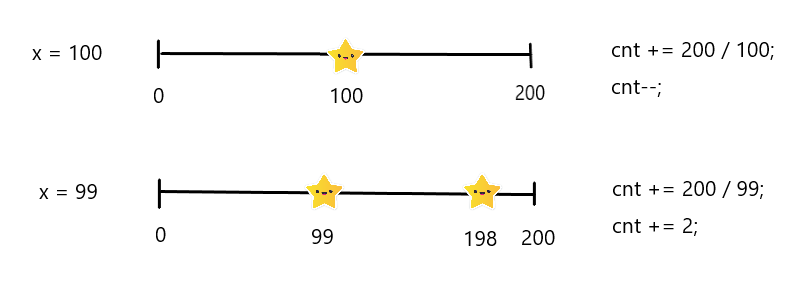
dist가 x로 나눠떨어지는 경우에는 몫에서 1을 빼줘야 새로 설치한 휴게소의 개수가 된다! (예외 처리 주의)

bool decision(int x){
	int cnt = 0; // 새로 세운 휴게소의 개수 
	
	for(int i = 1; i < arr.size(); i++){
		// 휴게소가 세워지지 않은 구간에 
		int dist = arr[i] - arr[i - 1];

		// x의 간격으로 새 휴게소를 세운다. 
		cnt += dist / x; 

		// 나눠떨어지는 경우에 대한 예외 처리 
		if(dist % x == 0) cnt--;
	}
	
	return cnt > M; 
}

최댓값 자체를 결정 함수의 매개변수 x로 잡고, 그것의 최솟값으로 구해야 하는 문제이므로 이해하기 조금 까다로웠던 거 같다.