문제
https://www.acmicpc.net/problem/1520
풀이
시간 초과 (DFS + 백트래킹)
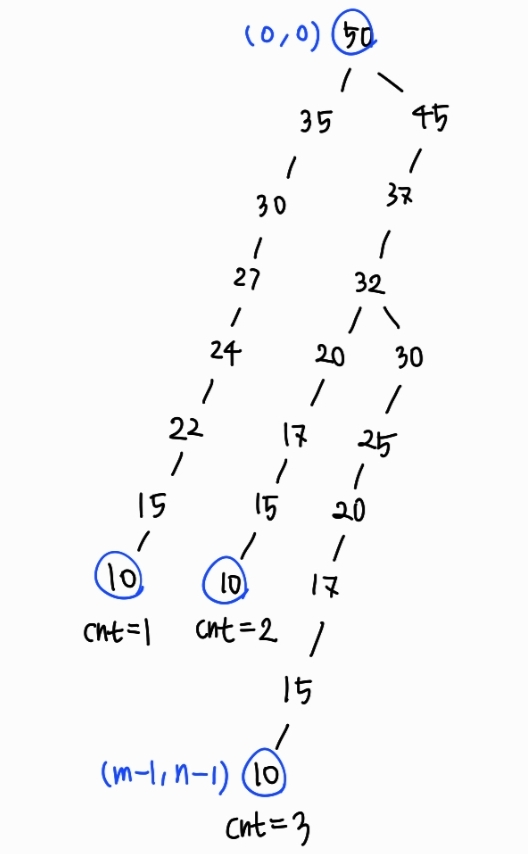
내리막길로 갈 수 있는 모든 경로를 DFS로 탐색했는데, 하나의 경로를 구하고 그 다음 경로를 구할 때 이전에 방문했던 칸을 재방문할 수 있기 때문에 visited 배열은 사용하지 않았다. 그리고 깊이 우선으로 탐색하다가 목적지인 (m - 1, n - 1)에 도달하면 더 이상 깊게 들어가지 않고 리턴하는, 백트래킹 방식으로 풀었다. (그리고 목적지에 도달할 때마다 경로의 수를 나타내는 cnt 갱신)
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
const int MAX = 501;
int height[MAX][MAX];
int m, n;
int cnt = 0;
int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, -1, 1};
void input() {
cin >> m >> n;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
cin >> height[i][j];
}
}
}
void dfs(int x, int y){
// 내리막길로 도착점에 도달할 때마다 cnt 갱신
if(x == m - 1 && y == n - 1){
cnt++;
return;
}
for(int i = 0; i < 4; i++){
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
// 현재보다 낮은 높이인지 검사
if(height[x][y] > height[nx][ny]){
dfs(nx, ny);
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
input();
dfs(0, 0);
cout << cnt;
return 0;
}M, N의 크기는 최대 500인데 각 칸마다 상하좌우를 탐색하므로, 목적지까지 도달하는 하나의 경로를 탐색하기 위해 최대 4 * 500 * 500 = 10,000번의 연산이 필요하다. 그런데 이 문제는 목적지까지 도달할 수 있는 여러 개의 경로를 모두 구해야 하므로 이보다 더 시간이 오래 걸린다.
DP (하향식, 메모이제이션)
https://yabmoons.tistory.com/340
https://hackids.tistory.com/109
DP는 메모리를 적절히 사용하여 시간복잡도를 비약적으로 단축시킬 수 있는 방법이다. 이미 계산된 결과를 별도의 메모리 공간에 저장하여 다시 계산하지 않도록 함으로써 연산 시간을 단축시킬 수 있다. DP는 일반적으로 하향식(top-down) 또는 상향식(bottom-up)으로 구현한다.
이 문제에는 DP의 메모이제이션 기법을 활용하여 시간복잡도를 줄일 수 있다. (하향식 접근)
우선 이미 계산된 결과를 저장할 dp 테이블을 만들어야 하는데, 이 문제에서는 각 칸마다 현재 칸에서 목적지까지 도달하는 경로의 개수를 저장할 것이다.
dp[a][b] = c 👉 (a, b)에서 (m - 1, n - 1)까지 c개의 경로로 도달할 수 있다.
탐색을 하다가 기존에 도달했던 좌표에 다시 도달한 경우, 다시 탐색할 필요 없이 dp 테이블에 저장된 경로의 개수를 그대로 사용하면 된다! 이를 메모이제이션 기법이라고 한다.
그리고 dp 테이블은 처음에 모두 '-1'로 초기화 시킬 것인데, 이는 '아직 이 좌표에서 목적지까지 가는 경로를 탐색해본 적이 없으니 탐색하세요' 라는 의미이다. 반면에, dp 테이블에 저장된 값이 0이면 '해당 좌표에서 목적지까지 갈 수 있는 경로가 0개'임을 의미한다.
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;
const int MAX = 501;
int height[MAX][MAX];
int dp[MAX][MAX];
int m, n;
int cnt = 0;
int dx[] = {0, 0, -1, 1};
int dy[] = {-1, 1, 0, 0};
void input() {
cin >> m >> n;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
cin >> height[i][j];
dp[i][j] = -1;
}
}
}
int dfs(int x, int y){
if(x == m - 1 && y == n - 1) return 1; // --- (a)
if(dp[x][y] != -1) return dp[x][y]; // --- (b)
dp[x][y] = 0;
for(int i = 0; i < 4; i++){
int nx = x + dx[i];
int ny = y + dy[i];
if(nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
if(height[x][y] > height[nx][ny]){
dp[x][y] += dfs(nx, ny);
}
}
return dp[x][y]; // --- (c)
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
input();
cout << dfs(0, 0);
return 0;
}위의 코드에서 재귀 호출에 따라 dp 테이블의 값이 어떻게 달라지는지 분석해보았다. (비어있는 칸은 -1로 초기화 되어 있다고 가정하자.)

dp[0][0]은 -1로 초기화 된 상태이므로 (b)에서 리턴되지 않고 다음 줄로 넘어간다.
dp[0][0] = 0로 다시 초기화 되고, 상하좌우에 자신보다 작은 값이 존재하는지 탐색한다.
자신보다 작은 값을 발견하면 그 위치에 대해 dfs 함수를 재귀 호출한다. 이런 식으로 depth가 깊어지면서 재귀 호출을 반복하다가 (3, 4)에 도달하면 1을 리턴한다. --- (a)
이 리턴값은 해당 함수를 재귀 호출했던 그때 당시의 dp[x][y]에 더해진다. 즉, 해당 함수를 재귀 호출하기 바로 이전 스택 프레임에 반영된다.
위의 그림에서는 함수가 리턴을 하면, 안쪽 프레임이 하나씩 삭제된다고 보면 된다. 그러면서 리턴값은 바로 바깥쪽 프레임에 반영된다.
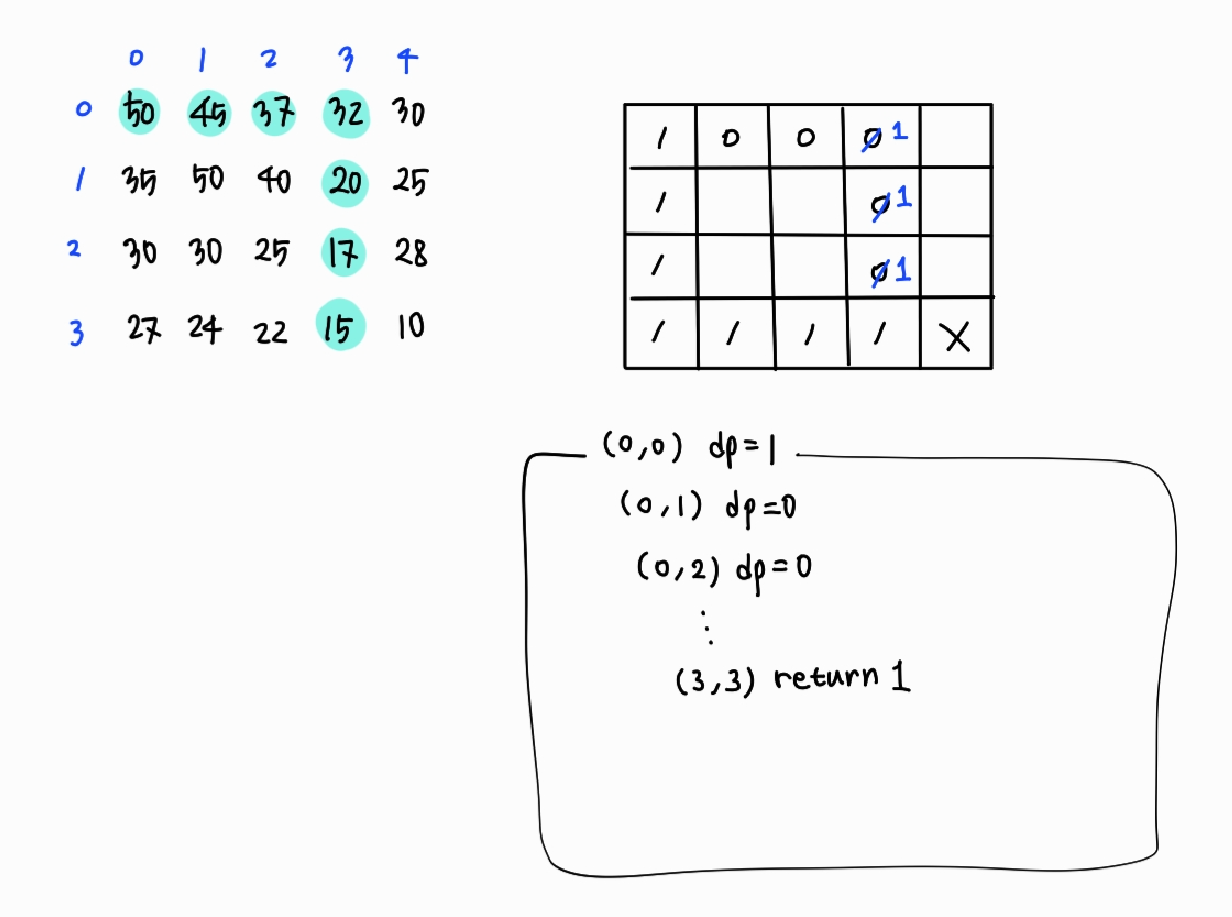
계속 리턴하다가 다시 (0, 0)으로 돌아오면 50보다 작은 값이 35 말고 45도 있기 때문에 이번에는 그쪽 방향으로 이동한다. 아까처럼 자신보다 작은 값을 발견할 때마다 재귀 호출을 반복하면서 dp 테이블을 채워나간다. 그러다가 (3, 3)에 도달하면 현재 dp 테이블에 채워진 값이 -1이 아니기 때문에 (b)에서 dp[x][y] 자체를 리턴한다. 그 리턴값은 바로 이전 스택 프레임에 반영된다.
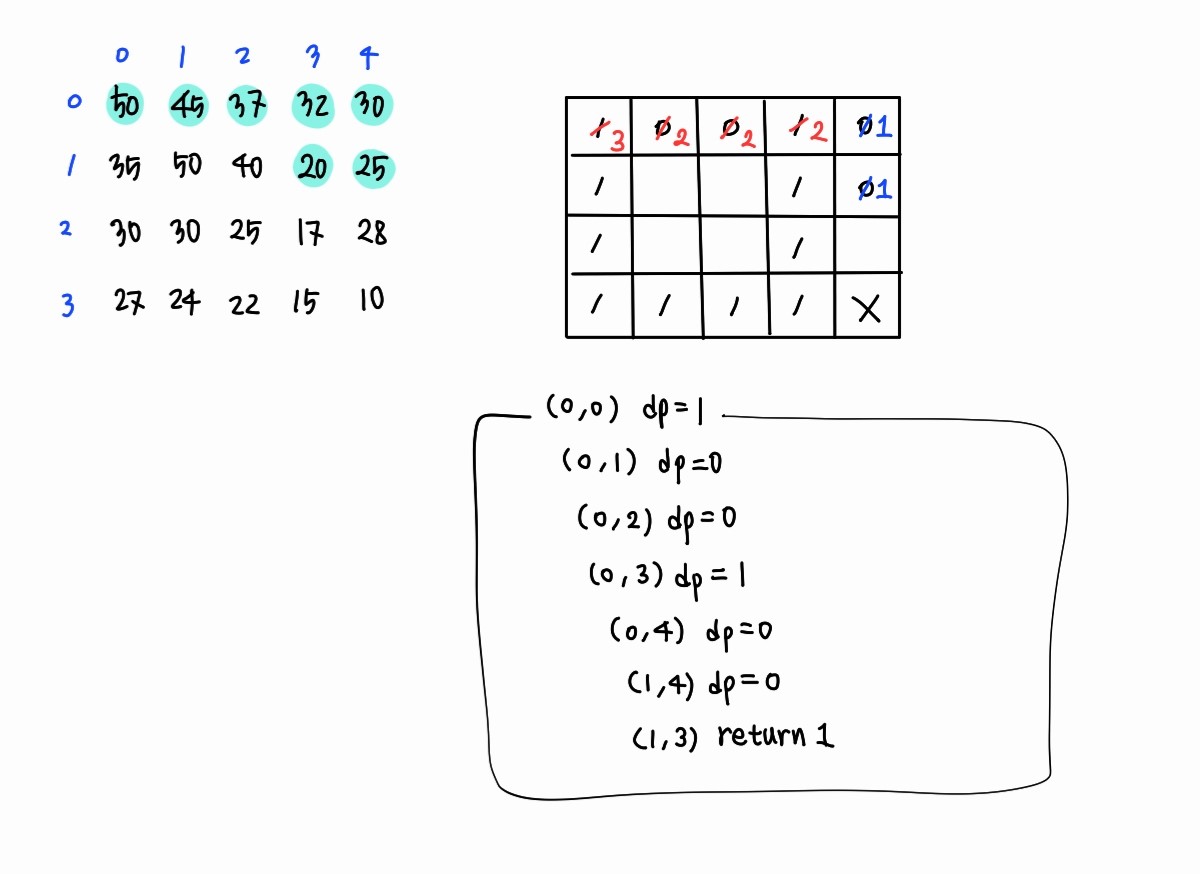
그리고 (0, 3)에 도달하면, 32보다 작은 값이 20 말고 30도 있기 때문에, 그쪽 방향으로 이동한다. 이번에도 자신보다 작은 값을 발견할 때마다 재귀 호출하다가 (1, 3)에 도달하면 dp 테이블에 이미 저장된 값이 있기 때문에 더 이상 탐색을 진행하지 않고 dp[1][3]을 그대로 반환한다.
재귀 호출을 했던 순서의 역방향으로 dp 테이블에 리턴값이 더해지게 되고, 결과적으로 (0, 0)으로 돌아와서 dp[0][0]에 저장된 3이 리턴되어 결과가 출력된다. --- (c)
이런 식으로 큰 문제를 작은 문제로 나눠서 작은 문제들의 해를 재귀적으로 구하고, 이를 취합하여 큰 문제의 해를 구하는 게 dp의 하향식 접근법이다. 그리고 한 번 계산된 결과를 기억하기 위해서 메모이제이션 기법을 이용한다. (이 문제에서는 현재 칸에서 목적지까지 도달하는 경로의 개수가 dp 테이블에 저장된다.)



