문제

https://www.acmicpc.net/problem/1613

---

풀이

이 문제를 처음 봤을 때 최근에 풀었던 위상 정렬 관련 문제가 가장 먼저 떠올랐다.

사이클이 존재하지 않는 방향 그래프에서 방향성에 거스르지 않고 노드의 순서를 결정할 때 사용하는 알고리즘이니까 위상 정렬을 이용하면 되지 않을까 생각했다.

그런데 계속 오답이 나와서 질문 게시판을 봤더니 생각지 못한 반례가 있었다.

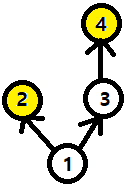
위의 그래프에 대해 위상 정렬을 수행하면 1 - 2 - 3 - 4 가 나오는데

실제로는 2번과 4번 사건의 전후 관계는 알 수 없다는 게 정답이다.

따라서, 이 문제는 위상 정렬로 접근하면 안 된다.

그렇다면, 특정한 두 사건의 전후 관계는 어떻게 구해야 할까?

바로, 모든 노드와 모든 노드 사이의 최단 경로를 구하는 플로이드 워셜 알고리즘을 이용하면 된다!

플로이드 워셜의 핵심 알고리즘은 다음과 같다.

각 단계마다 특정한 노드 k를 거쳐 가는 경우를 확인한다. 즉, a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사한다.

$D_{ab} = min(D_{ab}, D_{ak} + D_{kb})$

이를 활용하여 다음과 같이 그래프의 인접 행렬을 구성할 수 있다.

• graph[a][b] = -1 : a가 b보다 먼저 일어난 사건
• graph[b][a] = 1 : b가 a보다 나중에 일어난 사건

그리고 연결고리가 되는 사건 k를 통해 사건 i, j의 발생 순서도 결정할 수 있다.

• graph[i][k] == -1 && graph[k][j] == -1 → graph[i][j] = -1
• graph[i][k] == 1 && graph[k][j] == 1 → graph[i][j] = 1

#include <iostream>
#include <string> 
#include <cstring>
#include <sstream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;

const int MAX = 401;
int N, K, S;
int graph[MAX][MAX];
vector<pii> ans;

void input(){
	cin >> N >> K;

	for(int i = 0; i < K; i++){
		int a, b;
		cin >> a >> b;
		graph[a][b] = -1;
		graph[b][a] = 1;
	}

	cin >> S;
	for(int i = 0; i < S; i++){
		int x, y;
		cin >> x >> y;
		ans.push_back({x, y});
	}
}

void floyd(){
	// 경유점을 가장 바깥 for문에서 돌린다.
	for(int k = 1; k <= N; k++){
		for(int i = 1; i <= N; i++){
			for(int j = 1; j <= N; j++){
				if(i == j) continue;
				if(i == k || j == k) continue;
				
				if(graph[i][j] == 0){
					if(graph[i][k] == -1 && graph[k][j] == -1){
						graph[i][j] = -1;
					}
					else if(graph[i][k] == 1 && graph[k][j] == 1){
						graph[i][j] = 1;
					}
				}
			}
		}
	}
}

void solution(){
	floyd(); 

	for(auto p: ans){
		int a = p.first;
		int b = p.second;
		cout << graph[a][b] << "\n";
	}
}

int main()
{ 
	ios::sync_with_stdio(0);
	cin.tie(0);

	input();
	solution();
	
	return 0;
}

N이 최대 400으로 작은 편이기 때문에, O(N^3)으로도 시간 초과가 발생하지 않는다!