문제

https://www.acmicpc.net/problem/1865

때는 2020년, 백준이는 월드나라의 한 국민이다. 월드나라에는 N개의 지점이 있고 N개의 지점 사이에는 M개의 도로와 W개의 웜홀이 있다. (단 도로는 방향이 없으며 웜홀은 방향이 있다.)

웜홀은 시작 위치에서 도착 위치로 가는 하나의 경로인데, 특이하게도 도착을 하게 되면 시작을 하였을 때보다 시간이 뒤로 가게 된다. 웜홀 내에서는 시계가 거꾸로 간다고 생각하여도 좋다.

시간 여행을 매우 좋아하는 백준이는 한 가지 궁금증에 빠졌다. 한 지점에서 출발을 하여서 시간여행을 하기 시작하여 다시 출발을 하였던 위치로 돌아왔을 때, 출발을 하였을 때보다 시간이 되돌아가 있는 경우가 있는지 없는지 궁금해졌다. 여러분은 백준이를 도와 이런 일이 가능한지 불가능한지 구하는 프로그램을 작성하여라.

입력

첫 번째 줄에는 테스트케이스의 개수 TC(1 ≤ TC ≤ 5)가 주어진다.

그리고 두 번째 줄부터 TC개의 테스트케이스가 차례로 주어지는데 각 테스트케이스의 첫 번째 줄에는 지점의 수 N(1 ≤ N ≤ 500), 도로의 개수 M(1 ≤ M ≤ 2500), 웜홀의 개수 W(1 ≤ W ≤ 200)이 주어진다.

그리고 두 번째 줄부터 M+1번째 줄에 도로의 정보가 주어지는데 각 도로의 정보는 S, E, T 세 정수로 주어진다. S와 E는 연결된 지점의 번호, T는 이 도로를 통해 이동하는데 걸리는 시간을 의미한다.

그리고 M+2번째 줄부터 M+W+1번째 줄까지 웜홀의 정보가 S, E, T 세 정수로 주어지는데 S는 시작 지점, E는 도착 지점, T는 줄어드는 시간을 의미한다. T는 10,000보다 작거나 같은 자연수 또는 0이다.

두 지점을 연결하는 도로가 한 개보다 많을 수도 있다. 지점의 번호는 1부터 N까지 자연수로 중복 없이 매겨져 있다.

출력

TC개의 줄에 걸쳐서 만약에 시간이 줄어들면서 출발 위치로 돌아오는 것이 가능하면 YES, 불가능하면 NO를 출력한다.

예제

---

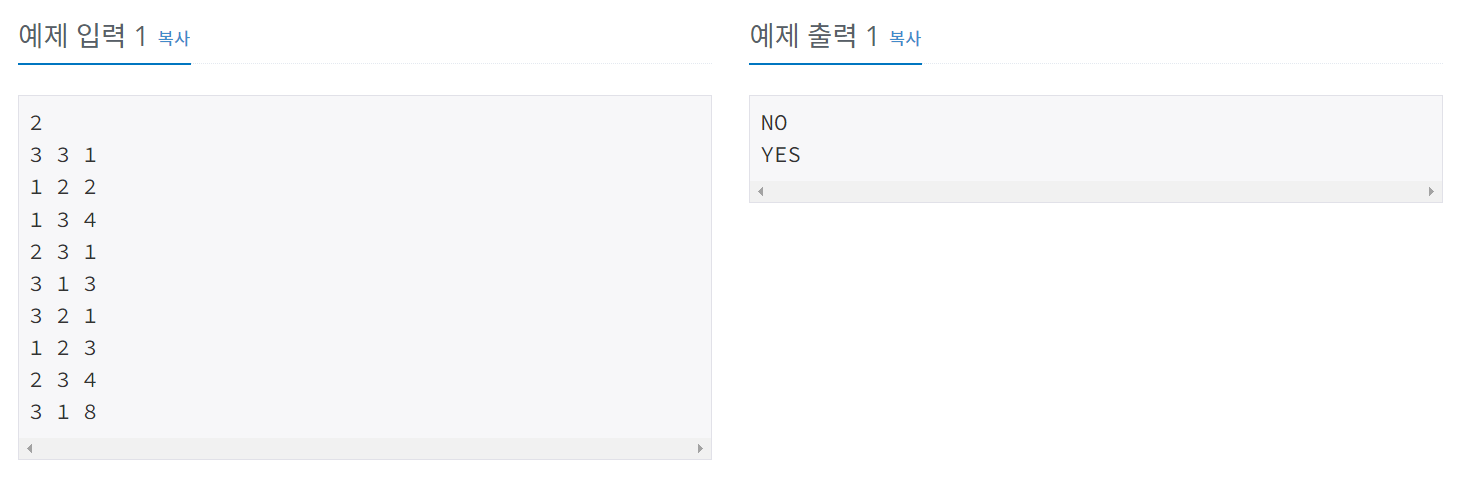
풀이

결국 이 문제는 음수 사이클이 존재하는지 확인하는 문제이다.

그리고 입력을 받을 때 주의해야 할 점은 '도로'는 양방향에 양의 간선이고, '웜홀'은 단방향에 음의 간선이라는 것이다.

또 주의해야 할 것은, d[from] == INF일 때 넘어가는 코드를 오히려 작성하면 안 된다는 것이다.

최단 거리 테이블인 d에 INF 값을 설정했던 이유는 단절된 노드를 파악하기 위함이었다. 따라서, 이 문제처럼 단순히 그래프에서 음수 사이클의 유무만 파악하고 싶을 때는 테이블 d의 초기값을 어떤 값으로 해줘도 상관없다. 왜냐하면, 우리가 알고 싶은 건 '최단 거리'가 아니라 '음수 사이클의 유무'이기 때문이다. 실제로 테이블 d를 -1로 초기화 해도 답이 통과된다.

시작 노드는 어떤 것으로 해도 상관없기 때문에 1번으로 설정했다.

관련 QnA
https://www.acmicpc.net/board/view/50494
https://www.acmicpc.net/board/view/54167

C++ 코드

#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <utility>
#define INF 1e9 
#define MAX 501 
using namespace std; 

int n, m, w; // 노드, 간선, 웜홀 개수 
int s, e, t; // 시작, 끝, 가중치 
vector<pair<int, pair<int, int>>> edges; 
long long d[MAX]; // 최단 거리 테이블 

bool bellmanFord(){ 
	d[1] = 0; // 시작 노드를 1번으로 고정 
	
	// (n-1)번의 라운드 반복 
	for(int i = 0; i < n; i++){ 
		// 매 반복마다 '모든 간선'을 하나씩 확인한다. 
		for(int j = 0; j < edges.size(); j++){ // 도로와 웜홀 모두 포함 
			int from = edges[j].first; 
			int to = edges[j].second.first; 
			int cost = edges[j].second.second;
            
            //if(d[from] == INF) continue; 
			
			// 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우 
			if(d[to] > d[from] + cost){ 
				d[to] = d[from] + cost; // 최단 거리 테이블 갱신 
				
				// n번째에도 최단 거리가 갱신된다면 음수 사이클 존재!  
				if(i == n - 1) return true;
			}
		}
	}
    
	return false;
}

int main()
{
	ios_base::sync_with_stdio(0);
	cin.tie(0);

	int tc; 
	cin >> tc;
	
	while(tc--){
		// 테스트 케이스마다 초기 데이터 초기화 
		fill_n(d, MAX, INF); 
		edges.clear(); 
		
		cin >> n >> m >> w; 

		// 도로는 양방향, 양수 간선 
		for(int i = 0; i < m; i++){
			cin >> s >> e >> t;
			edges.push_back({s, {e, t}}); 
			edges.push_back({e, {s, t}}); 
		}

		// 웜홀은 단방향, 음수 간선 
		for(int i = 0; i < w; i++){ 
			cin >> s >> e >> t; 
			edges.push_back({s, {e, -t}}); 
		}

		// 음수 사이클이 존재하는지 확인
		if(bellmanFord()) cout << "YES\n";
		else cout << "NO\n";
	}
	
	return 0; 
}

d의 초기값을 -1로 하든, 무한대로 하든 상관없이 통과된다.