문제

https://www.acmicpc.net/problem/1904

---

풀이

구현

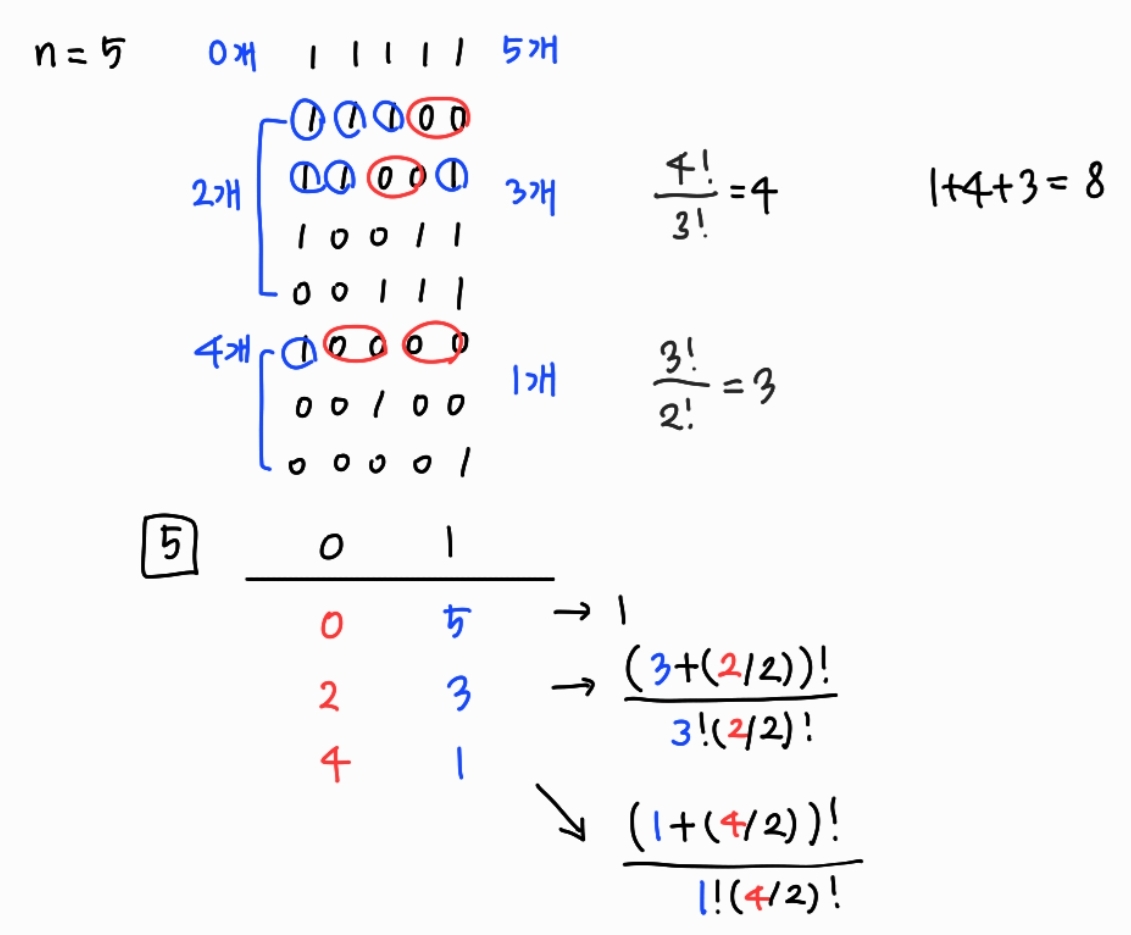
0의 개수와 1의 개수에 따라 같은 것이 있는 순열로 경우의 수를 구해보았다,,

#include <iostream>
#include <vector> 
#include <algorithm>
using namespace std; 

int n; 

// 같은 것이 있는 순열로 경우의 수 계산 
int factorial(int x, int y){ // 0과 1의 개수 
	int a = 1, b = 1, c = 1; 

	// (y + x/2)! 
	for(int i = 1; i <= y + x/2; i++){
		a *= i; 
	}

	// y! 
	for(int i = 1; i <= y; i++){
		b *= i; 
	}

	// (x/2)! 
	for(int i = 1; i <= x/2; i++){
		c *= i; 
	}

	return a / (b * c); 
} 

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n; 

	// 길이가 n인 1과 00으로 만들 수 있는 2진 수열의 개수 
	int ans = 0; 

	for(int i = 0; i <= n; i += 2){ // 0의 개수 
		int j = n - i; // 1의 개수 

		if(i == 0 || j == 0){
			ans += 1; 
			continue; 
		}

		// 각 케이스에 대한 수열의 개수 구해서 더하기 
		ans += factorial(i, j); 
	}
	
	cout << ans % 15746; 
	
	return 0; 
}

규칙성 발견 (피보나치)

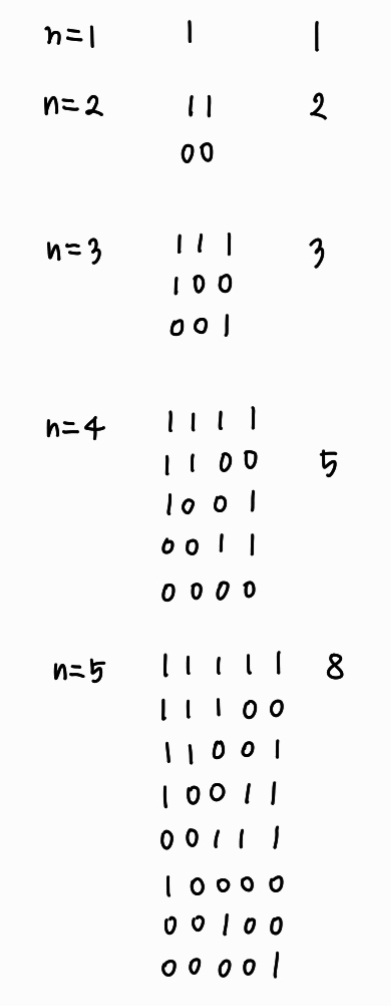
경우의 수를 계산해나가다 보면, 혹시 피보나치 수열인가..? 라고 짐작해볼 수 있다.

1과 00만으로 길이가 n인 2진 수열을 만들려면,

1. (n-2)번째 자리에 00이 오는 경우
2. (n-1)번째 자리에 1이 오는 경우

이 두가지 밖에 없다. (n-2)번째 자리에 11이 오는 경우는 2번에 포함된다. 따라서 다음과 같이 피보나치 수열과 동일한 점화식이 나온다.

d[i] = d[i - 2] + d[i - 1]

그리고 이 문제에서 주의해야 할 점은 N이 최대 100만이기 때문에, N번째 피보나치 수를 구할 때 int 범위를 넘어선다. 따라서 dp 테이블은 long long 타입이어야 하고, 원래 값에서 15746으로 나눈 나머지를 저장해줘야 한다.

top-down (하향식)

#include <iostream>
#include <vector> 
#include <algorithm>
#define MAX 1000001 
using namespace std; 

long long d[MAX] = {0, 1, 2}; 
int n; 

long long fibo(int x){  
	if(x == 1 || x == 2) return x; 
	
	if(d[x] != 0){ 
		return d[x]; 
	}
	
	d[x] = (fibo(x - 1) + fibo(x - 2)) % 15746; 
	return d[x]; 
}

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n; 
	cout << fibo(n); 
	
	return 0; 
}

bottom-up (상향식)

#include <iostream>
#include <vector> 
#include <algorithm>
#define MAX 1000001 
using namespace std; 

long long d[MAX] = {0, 1, 2}; 
int n; 

int main() 
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n; 

	for(int i = 3; i <= n; i++){ 
		d[i] = (d[i - 2] + d[i - 1]) % 15746; 
	}
	
	cout << d[n]; 
	
	return 0; 
}

반복문을 이용한 상향식이 재귀함수를 이용한 하향식보다 시간과 메모리가 더 적게 드는 것을 확인할 수 있다.