문제
https://www.acmicpc.net/problem/2176
풀이
역방향 다익스트라, DP를 이용한 문제였다. 완전 처음 보는 유형.. 역시 골드 2는 어렵다.
처음 문제를 봤을 때 'T에 가까워지며 이동하는 경로'가 무엇인지 정의 내리는 게 어려웠다. 이것부터 명확하게 파악해야 그 다음 단계를 진행할 수 있는데 기준이 좀 모호하다는 느낌이 들었다.
그리고 가능한 모든 합리적인 경로의 개수를 구하는 거니까 백트래킹 문제인가 ..? 했지만 전혀 아니었다 ㅎ.ㅎ
이 블로그가 그나마 설명이 제일 이해가 잘 되어서 참고를 많이 했다. 해당 포스팅에서도 문제 자체가 헷갈리는 편이라고 한다. (나만 그런 게 아니었군,,)
여러 포스팅에서 합리적인 이동경로를 다음과 같이 정의하고 있다. (문제 자체에서 설명이 좀 더 있었으면 좋겠다는 생각이 든다 🥲)
- S에서 T로 가는 거리 : d
- S에서 U를 거쳐서 T로 갈 때, U에서 T로 가는 거리 : e
- d > e 여야 합리적인 이동경로이다.
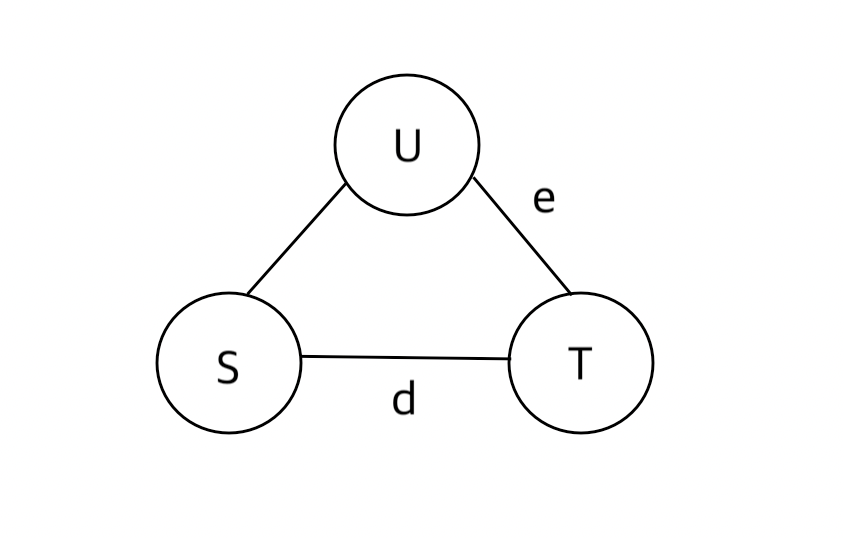
그렇다면, 아래 예시에서 1 -> 2로 가는 합리적인 이동 경로는 몇 개일까?
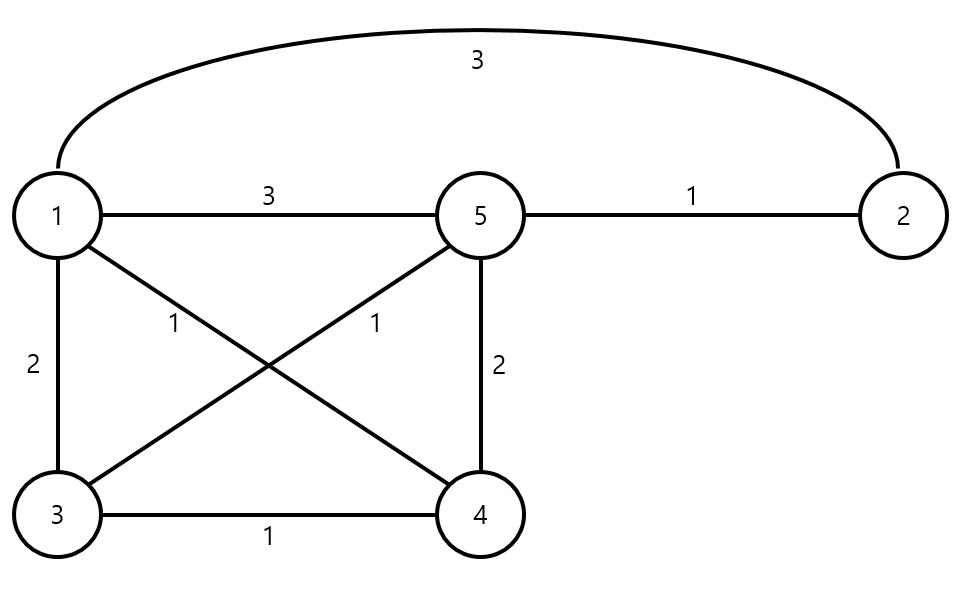
가능한 모든 경로는 다음과 같다.
- 1 -> 2
- 1 -> 3 -> 4 -> 5 -> 2
- 1 -> 3 -> 5 -> 2
- 1 -> 4 -> 5 -> 2
- 1 -> 4 -> 3 -> 5 -> 2
- 1 -> 5 -> 2
이 중에서 최단 경로는 [1 -> 2]
합리적인 이동 경로는 [1 -> 2], [1 -> 3 -> 5 -> 2], [1 -> 5 -> 2] 만 해당한다.
[1 -> 2] 경로의 최단 거리가 3인데
[1 -> ... -> 4 -> ... -> 2] 이렇게 4번을 거치게 되면
[4 -> 2] 경로의 최단 거리도 3이어서 합리적인 이동 경로가 될 수 없다.
예를 들어 [1 -> 3 -> 5 -> 2] 같은 경우에는 최단 거리는 아니지만
[3 -> 2] 경로의 최단 거리가 2이므로 합리적인 이동 경로라고 볼 수 있다.
역방향 다익스트라
[1 -> 4] 같은 경우는 합리적인 이동 경로가 아니라는 것을 바로 알아차리기 위해서
T에서 모든 노드까지의 최단 거리를 구해보자. (역방향 다익스트라 진행)
dist[i] : T에서 i번 노드까지의 최단 거리 (이 문제에서 T는 2로 고정)
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| dist | 3 | 0 | 2 | 3 | 1 |
위와 같이 최단 거리 테이블을 채울 수 있다.
DP
다음과 같이 dp 테이블을 정의하고 dist 배열에서 '최단 거리가 짧은 노드부터' 먼저 탐색해보자.
- dp[i] : i번 노드에서 T까지의 합리적인 이동 경로 개수
- dp[2] = 1 로 초기화
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| dp | 1 |
최단 거리가 가장 짧은 5번 노드
5번 노드로 진입하는 노드는 1, 2, 3, 4가 있지만, 이 중에서 최단 거리가 5번보다 짧은 노드는 2번밖에 없다.
=> dp[5] = dp[2] = 1
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| dp | 1 | 1 |
3번 노드
3번 노드로 진입하는 노드는 1, 4, 5가 있지만, 이 중에서 최단 거리가 3번보다 짧은 노드는 5번밖에 없다.
=> dp[3] = dp[5] = 1
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| dp | 1 | 1 | 1 |
1번 노드
1번 노드로 진입하는 노드는 2, 3, 4, 5가 있지만, 이 중에서 최단 거리가 1번보다 짧은 노드는 2, 3, 5번이 있다.
=> dp[1] = dp[2] + dp[3] + dp[5] = 3
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| dp | 3 | 1 | 1 | 1 |
실제로 가능한 합리적인 이동 경로 3가지는 다음과 같다. (2, 3, 5번에서 들어오는 경우)
- [1 <- 2]
- [1 <- 3 <- 5 <- 2]
- [1 <- 5 <- 2]
4번 노드
4번 노드로 진입하는 노드는 1, 3, 5가 있지만, 이 중에서 최단 거리가 4번보다 짧은 노드는 3, 5번이 있다.
=> dp[4] = dp[3] + dp[5] = 2
| i | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| dp | 3 | 1 | 1 | 2 | 1 |
최종
1 -> ... -> 2 로 가는 합리적인 이동경로 개수를 구해야 하므로 dp[1]을 출력한다.
C++ 코드
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
#include <map>
#include <set>
#include <queue>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int MAX = 1001;
const int INF = 1e9;
vector<pii> graph[MAX];
int dist[MAX];
int dp[MAX];
int N, M;
// T에서 모든 노드까지의 최단 거리 구하기
// 합리적인 이동 경로 개수를 저장하는 DP 테이블 채우기
void dijkstra(int t) {
priority_queue<pii, vector<pii>, greater<pii>> pq;
pq.push({0, t}); // 거리를 기준으로 최소 힙
dist[t] = 0;
dp[t] = 1;
while(!pq.empty()){
auto cur = pq.top();
pq.pop();
int d = cur.first;
int now = cur.second;
// 현재 노드에 대해 처리한 경우 패스
if(d > dist[now]) continue;
// 인접 노드 검사
for(auto edge: graph[now]){
int adj = edge.first;
int cost = edge.second;
int nd = d + cost;
if(dist[adj] > nd){
// 최단 거리 테이블 갱신
dist[adj] = nd;
pq.push({nd, adj});
}
// 현재 노드보다 최단 거리가 짧은 경우
// 합리적인 이동 경로에 포함시키고 DP 테이블 갱신
if(d > dist[adj]){
dp[now] += dp[adj];
}
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> M;
fill(dist, dist + MAX, INF);
for(int i = 0; i < M; i++){
int a, b, c;
cin >> a >> b >> c;
graph[a].push_back({b, c});
graph[b].push_back({a, c});
}
dijkstra(2);
cout << dp[1];
return 0;
}
