문제
https://www.acmicpc.net/problem/2293
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
입력
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000)
다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 경우의 수를 출력한다. 경우의 수는 2^31 (int의 최댓값) 보다 작다.
예제

풀이
참고: https://transferhwang.tistory.com/342
동전 0 문제는 그리디 알고리즘으로 최적해를 구할 수 있지만, 이 문제는 동전의 가치가 서로 배수 관계라는 조건이 없기 때문에 DP로 최적해를 구해야 한다.
문제의 예제를 통해 차근차근 전체 경우의 수를 따져보고, 그로부터 규칙성을 파악하여 점화식을 도출해보자!
1, 2, 5원을 조합하여 10원을 만드는 경우의 수를 구해보자.
우선, 1원으로 n원을 만드는 경우의 수는 다음과 같다.
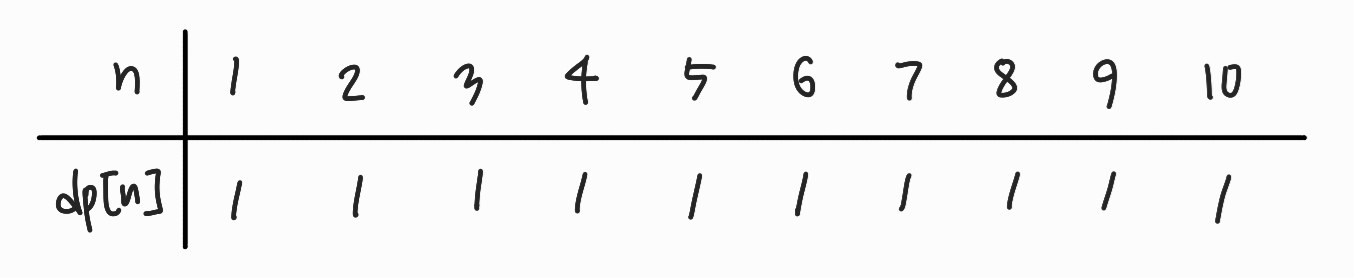
다음으로, 1원과 2원을 조합하여 n원을 만드는 경우의 수는 다음과 같다.
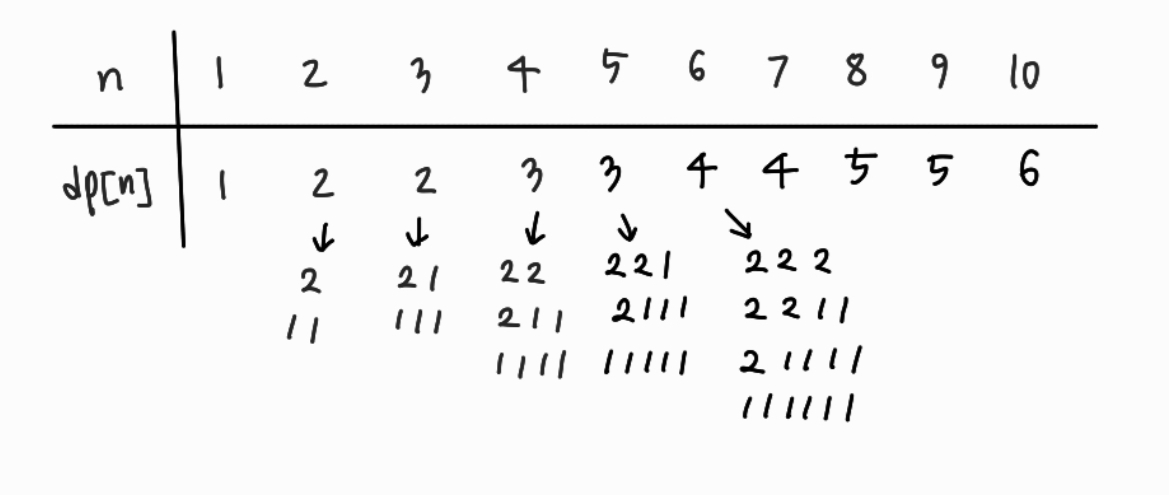
그러면 다음과 같은 규칙성을 발견할 수 있다.

즉, 새로 갱신되는 dp[n]의 값은 이전의 dp[n]의 값에 dp[n - 현재 사용한 동전의 종류 크기] 가 되는 것이다.
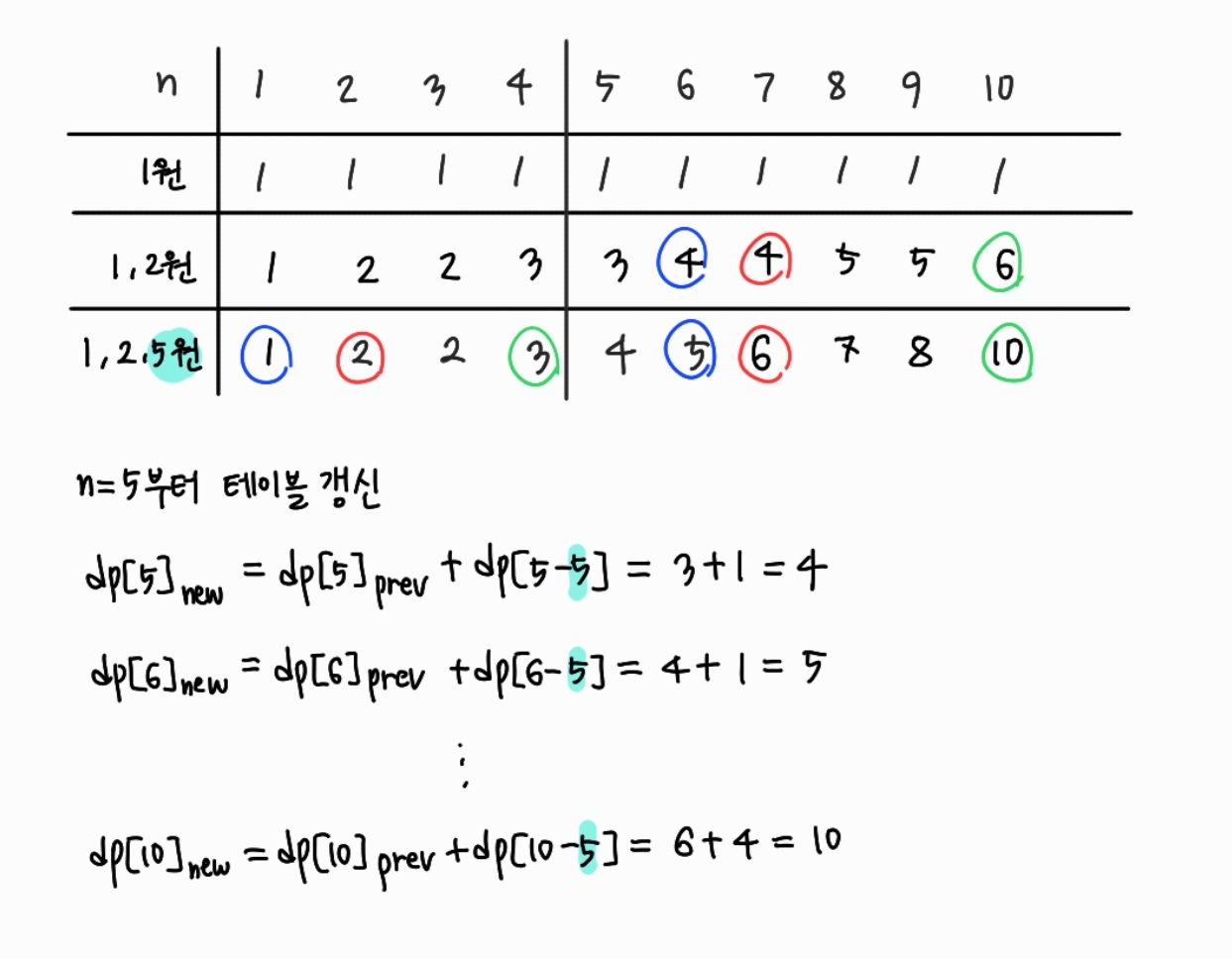
결국, 1, 2, 5원으로 10원을 만드는 경우의 수는 10개라는 것을 알 수 있다. 아 그리고 주의해야 할 것은, dp[0]은 주어진 동전을 갖고 0원을 만드는 경우의 수인데, 이것은 결국 어떤 동전도 사용하지 말아야 하므로 경우의 수는 1이다. 따라서 dp[0]은 1이다.
v가 n개의 동전 종류를 저장하는 배열이라고 했을 때, 위에서 발견한 규칙성에 따라 다음과 같이 점화식을 작성할 수 있다.
dp[n] = dp[n] + dp[n - v[i]]
#include <iostream>
#include <vector>
using namespace std;
int dp[10001];
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
int n, k;
cin >> n >> k;
vector<int> v(n + 1);
for(int i = 1; i <= n; i++){
cin >> v[i];
}
dp[0] = 1;
// 동전의 종류마다 최대 k번까지 경우의 수가 갱신된다.
for(int i = 1; i <= n; i++){
// 동전의 크기를 첫번째 동전 크기부터 k원까지 1씩 늘리면서
for(int j = v[i]; j <= k; j++){
// 점화식에 따라 테이블 갱신
dp[j] += dp[j - v[i]];
}
}
cout << dp[k];
return 0;
}


덕분에 좋은 내용 잘 보고 갑니다
감사합니다.