문제

https://www.acmicpc.net/problem/2343

---

풀이

최적화 문제를 결정 문제로 바꾸고 이분탐색으로 문제를 해결하는 파라메트릭 서치를 적용해보자!

• 최적화 문제 : N개의 강의를 M개의 블루레이에 나눠서 담으려면, 각 블루레이의 크기는 최소 얼마여야 하는가?
• 결정 문제 : 블루레이의 크기가 x일 때, N개의 강의를 M개의 블루레이에 나눠서 담을 수 있는가?

블루레이 크기가 x일 때, N개의 강의를 담기 위해 필요한 블루레이 개수를 cnt라고 하면

다음과 같은 반비례 관계가 성립함을 알 수 있다.

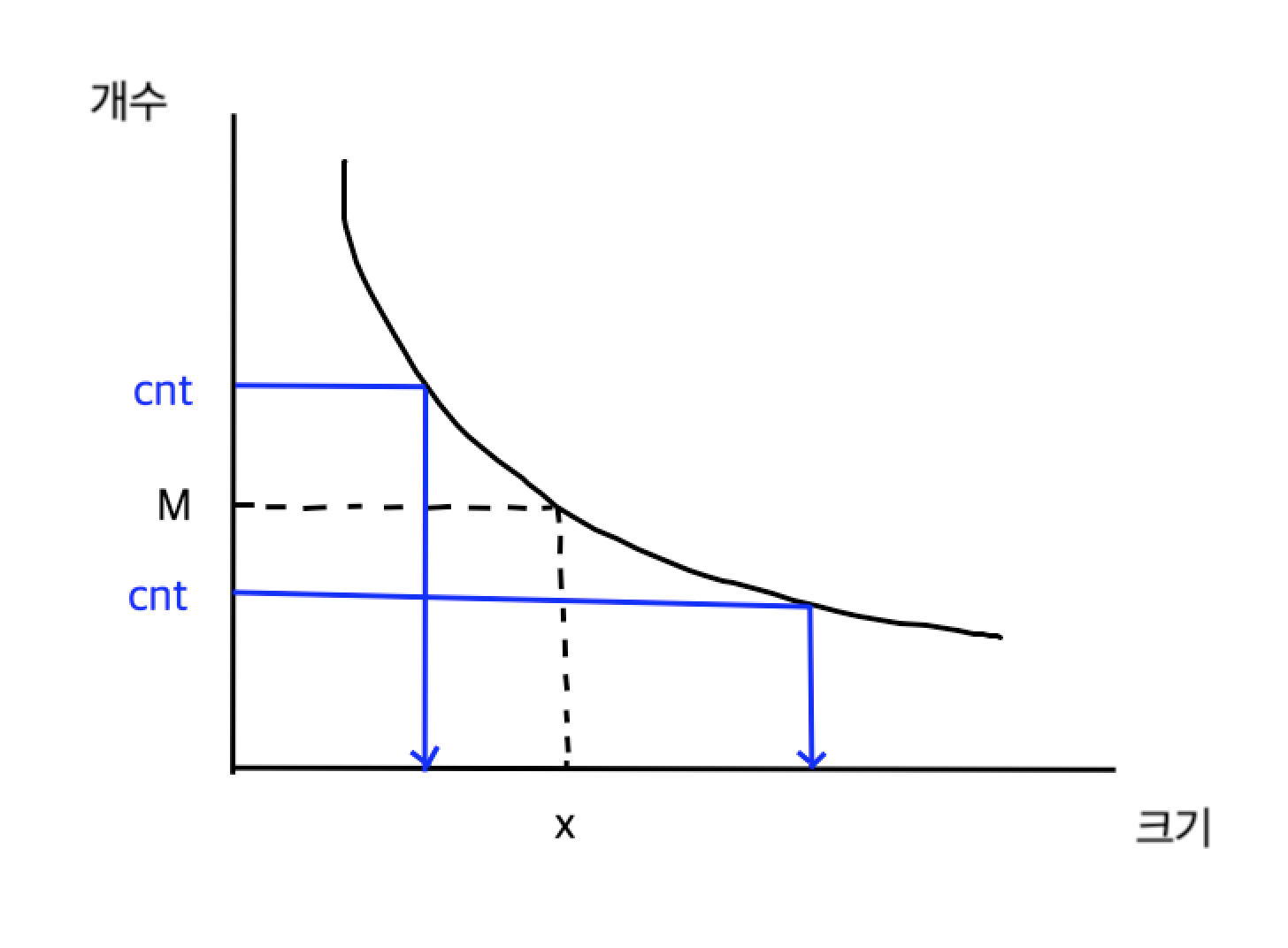
• cnt > M : x 늘리기
• cnt == M : x 줄이기 (최소화 시키기 위해)
• cnt < M : x 줄이기

예를 들어, 주어진 예제에서

9 3
1 2 3 4 5 6 7 8 9

x = 10
1 2 3 4 / 5 / 6 / 7 / 8 / 9 -> 최소 6개 필요 (cnt > M) -> x 늘리기

x = 16
1 2 3 4 5 / 6 7 / 8 / 9 -> 최소 4개 필요 (cnt > M) -> x 늘리기

x = 17
1 2 3 4 5 / 6 7 / 8 9 -> 최소 3개 필요 (cnt == M) -> x 줄이기
👉 여기서 더 줄이면 M개 초과이므로 x = 17이 M개를 담을 수 있으면서도 최소 크기 !!

x = 20
1 2 3 4 5 / 6 7 / 8 9 -> 최소 3개 필요 (cnt == M) -> x 줄이기

따라서, 블루레이 크기의 최솟값을 left, 최댓값을 right 포인터로 가리키고 탐색 범위를 절반씩 줄여나가면서 M개의 강의를 담을 수 있으면서도 최소 크기인 x를 구하면 된다.

📌 블루레이 크기의 최솟값은?
예를 들어 1이 최소라고 하면 1분이 넘는 강의는 애초에 블루레이에 담을 수가 없기 때문에, 최솟값은 주어진 강의 시간 중에 최댓값이 되어야 한다.

📌 블루레이 크기의 최댓값은?
모든 강의 시간의 합을 블루레이 크기로 잡으면, 1개의 블루레이에 N개를 전부 담을 수 있으므로 최댓값은 N개의 강의 시간의 합이 된다.

시간초과

다음과 같이 크기의 최솟값을 1로 잡으면 시간초과가 발생한다.

#include <iostream>
#include <string> 
#include <cstring>
#include <sstream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
#include <set>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;

int N, M; 
queue<int> lessons;

// 블루레이 크기가 x일 때 
// N개의 강의를 담기 위해 필요한 개수는 M개 이하인가? 
bool decision(int x){
	queue<int> q(lessons); // 원소 전체 복사 
	
	int sum = 0, cnt = 0;
	while(!q.empty()){
		if(sum + q.front() <= x){ 
			sum += q.front(); 
			q.pop(); 
			if(q.empty()) cnt++; 
		}else{
			cnt++; 
			sum = 0; 
		}
	}
	
	return cnt <= M;
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> N >> M; 

	int sum = 0;
	for(int i = 0; i < N; i++){
		int x; 
		cin >> x;
		lessons.push(x);
		sum += x;
	}

	int left = 1, right = sum;
	int ans = 1e9;
	while(left <= right){
		int mid = (left + right) / 2;
		if(decision(mid)){
			ans = min(ans, mid);
			right = mid - 1;
		}else{
			left = mid + 1;
		}
	}
	
	cout << ans;
	
	return 0;
}

이분탐색 범위 줄이기

블루레이 크기의 최솟값을 N개의 강의 시간 중에 최댓값으로 잡으니까 시간 초과가 발생하지 않았다.

#include <iostream>
#include <string> 
#include <cstring>
#include <sstream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
#include <set>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;

int N, M; 
queue<int> lessons;

// 블루레이 크기가 x일 때 
// N개의 강의를 담기 위해 필요한 개수는 M개 이하인가?
bool decision(int x){
	queue<int> q(lessons); // 원소 전체 복사 
	
	int sum = 0, cnt = 0;
	while(!q.empty()){
		if(sum + q.front() <= x){ 
			sum += q.front(); 
			q.pop(); 
			if(q.empty()) cnt++; 
		}else{
			cnt++; 
			sum = 0; 
		}
	}
	
	return cnt <= M;
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> N >> M; 

	int sum = 0;
	int longestLesson = 0;
	
	for(int i = 0; i < N; i++){
		int x; 
		cin >> x;
		lessons.push(x);
		
		sum += x;
		longestLesson = max(x, longestLesson);
	}

	int left = longestLesson; // 크기의 최솟값 
	int right = sum; // 크기의 최댓값 -> 개수 1 
	
	int ans = 1e9;
	while(left <= right){
		int mid = (left + right) / 2;
		if(decision(mid)){
			ans = min(ans, mid);
			right = mid - 1;
		}else{
			left = mid + 1;
		}
	}
	
	cout << ans;
	
	return 0;
}

이분탐색 범위의 크기를 K (right - left) 라고 하면, 결정 함수의 시간복잡도가 O(N)이므로

총 시간 복잡도는 O(N * logK) 으로 예상할 수 있다.

큐 대신 배열 사용

참고: https://chanhuiseok.github.io/posts/baek-22/

결정 함수에서 매번 큐에 전체 원소를 복사하고 pop 하는 연산이 있는데, 배열을 이용하면 이런 연산을 생략할 수 있기 때문에 다음과 같이 코드를 개선했다.

#include <iostream>
#include <string> 
#include <cstring>
#include <sstream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <queue>
#include <map>
#include <set>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;

int N, M; 
vector<int> lessons;

bool decision(int x){
	int sum = 0, cnt = 0;
	
	for(auto time: lessons){
    	// x를 넘는 지점에서 cnt 갱신 
		if(sum + time > x){ 
			cnt++;
			sum = 0; 
		}
        
        // if문과 상관없이 매번 실행 
		sum += time; 
	}
	
    // for문에서 처리되지 않은 강의들에 대해 cnt 갱신
	if(sum != 0) cnt++;  
	
	return cnt <= M;
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> N >> M; 

	int sum = 0;
	int longestLesson = 0;
	
	for(int i = 0; i < N; i++){
		int x; 
		cin >> x;
		lessons.push_back(x);
		
		sum += x;
		longestLesson = max(x, longestLesson);
	}

	int left = longestLesson; // 크기의 최솟값 
	int right = sum; // 크기의 최댓값 -> 개수 1 
	
	int ans = 1e9;
	while(left <= right){
		int mid = (left + right) / 2;
		if(decision(mid)){
			ans = min(ans, mid);
			right = mid - 1;
		}else{
			left = mid + 1;
		}
	}
	
	cout << ans;
	
	return 0;
}

• 큐를 사용한 풀이
  

• 배열을 사용한 풀이
  

공간복잡도와 시간복잡도 모두 줄어들었다!