문제

https://www.acmicpc.net/problem/2344

---

풀이

거울에 의한 방향 전환은 그래프 탐색에서 자주 사용되는 dx, dy 배열을 이용하면 되겠다고 생각했는데

상자의 테두리를 따라 1 ~ 2(N + M)까지의 숫자를 어떻게 표시해야 할지 고민이었다.

0행, 0열, N-1행, M-1열 원소들에 대해서만 테두리의 숫자들을 저장하게 해야 하나..?

구현 방법이 복잡할 거 같았다. 상자의 모서리에 위치한 원소들은 값을 2개 가지고 있어야 하기 때문이다.

결국 다른 사람 풀이를 참고하니까 굉장히 쉬운 방법이 있었다!

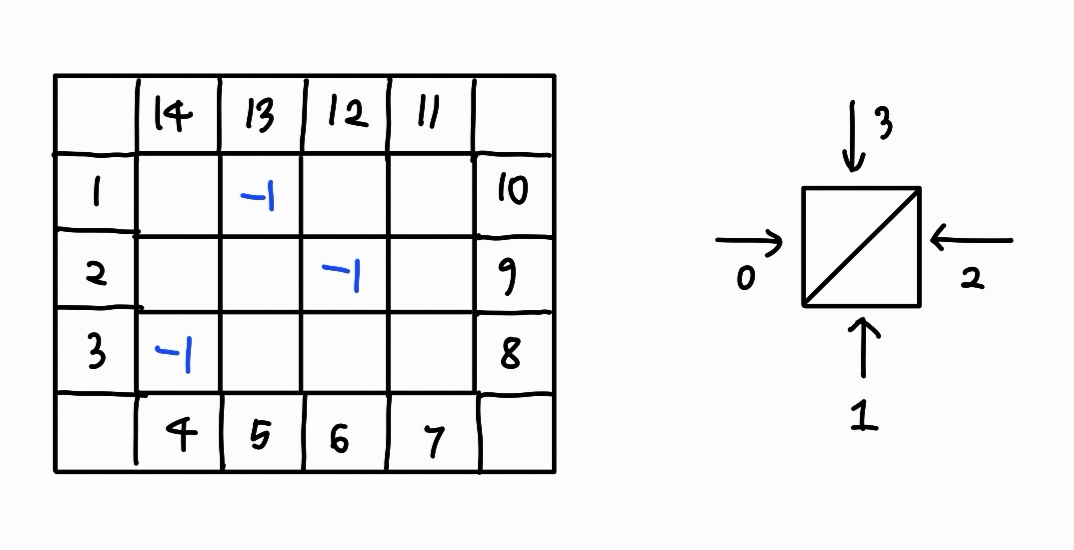
이렇게 배열의 크기를 (N + 2) x (M + 2) 로 확장하면, 상자의 테두리에 있는 구멍들의 번호를 쉽게 표시할 수 있다!

그리고 정답을 구할 때도 1 이상의 숫자가 있는 위치에 도달하면 탐색을 종료하면 된다.

구멍 번호를 나타내는 1과 헷갈리지 않도록 거울의 위치는 -1로 표시해준다.

#include <iostream>
#include <string> 
#include <cstring>
#include <sstream>
#include <algorithm>
#include <vector>
#include <cmath>
#include <stack>
#include <queue>
#include <map>
#include <set>
#include <unordered_set>
#include <unordered_map>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;

const int MAX = 1005;
int graph[MAX][MAX];
int N, M; // 세로, 가로

// 우 상 좌 하 
int dx[] = {0, -1, 0, 1};
int dy[] = {1, 0, -1, 0};

void input() {
	cin >> N >> M;

	for(int i = 0; i < N + 2; i++){
		for(int j = 0; j < M + 2; j++){
			if(i == 0 || i == N + 1) continue;
			if(j == 0 || j == M + 1) continue;
			cin >> graph[i][j];

			if(graph[i][j] == 1){
				graph[i][j] = -1; 
			}
		}
	}
}

void markHole() {
	// 0열
	for(int i = 1; i <= N; i++){
		graph[i][0] = i;
	}

	// N + 1행
	for(int i = 1; i <= M; i++){
		graph[N + 1][i] = N + i;
	}

	// M + 1열
	for(int i = N; i >= 1; i--){
		graph[i][M + 1] = (N + M) + (N - i + 1);
	}

	// 0행
	for(int i = M; i >= 1; i--){
		graph[0][i] = (2 * N + M) + (M - i + 1);
	}
}

int changeDirection(int dir){
	if(dir == 0) return 1; // 우 -> 상 
	else if(dir == 1) return 0; // 상 -> 우 
	else if(dir == 2) return 3; // 좌 -> 하 
	else return 2; // 하 -> 좌 
}

int dfs(int x, int y, int dir) {
	int nx = x + dx[dir];
	int ny = y + dy[dir];
	
	if(graph[nx][ny] >= 1){
		return graph[nx][ny];
	}

	if(graph[nx][ny] == -1){
		return dfs(nx, ny, changeDirection(dir));
	}else{
		return dfs(nx, ny, dir);
	}
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	input();
	
	markHole();

	// 0열 
	for(int i = 1; i <= N; i++){
		cout << dfs(i, 0, 0) << " ";
	}

	// N+1행 
	for(int i = 1; i <= M; i++){
		cout << dfs(N + 1, i, 1) << " ";
	}

	// M+1열 
	for(int i = N; i >= 1; i--){
		cout << dfs(i, M + 1, 2) << " ";
	}

	// 0행 
	for(int i = M; i >= 1; i--){
		cout << dfs(0, i, 3) << " ";
	}
	
	return 0;
}

인접 행렬을 기반으로 그래프를 구성했으므로 DFS 함수의 시간복잡도는 O(N^2)이라고 보면 된다.