문제
https://www.acmicpc.net/problem/2493
풀이
왼쪽에 자신보다 높은 탑이 있다면 레이저가 수신되며, 그런 탑이 여러 개라면 자신과 더 가까이 있는 탑이 수신하게 된다.
그런데 이 문제의 조건을 보면, N의 최대 크기가 '50만'이기 때문에 O(N^2)의 시간복잡도로 풀면 시간초과가 날 수밖에 없다.
시간 초과 (브루트포스)
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <stack>
#include <set>
using namespace std;
const int MAX = 500001;
int tower[MAX];
int answer[MAX];
int main(void) {
ios::sync_with_stdio(0);
cin.tie(0);
int N;
cin >> N;
for(int i = 0; i < N; i++){
cin >> tower[i];
}
// 왼쪽에서 오른쪽으로 이동
for(int i = 0; i < N; i++){
int curHeight = tower[i];
if(i == 0) continue;
// 자신의 왼쪽에 자신보다 높은 탑이 있는지 탐색
for(int j = i - 1; j >= 0; j--){
if(tower[j] > curHeight){
answer[i] = j + 1;
break;
}
}
}
for(int i = 0; i < N; i++){
cout << answer[i] << " ";
}
return 0;
}시간복잡도를 줄이기 위해서, 자신보다 높은 탑이 왼쪽에 있는지 탐색하는 코드를 이분 탐색으로 구해야 하나? 했는데, 이분 탐색은 정렬된 배열에 대해서만 적용할 수 있기 때문에 이 문제에서는 사용할 수 없었다.
Monotonic Stack (단조 스택)
Monotonic Stack은 원소가 단조 증가/감소 순으로 정렬되어 있는 스택을 의미한다.
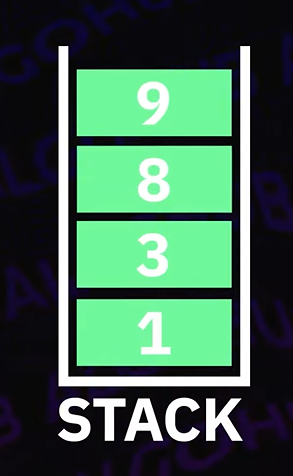
Monotonic Increasing (단조 증가)

Monotonic Decreasing (단조 감소)
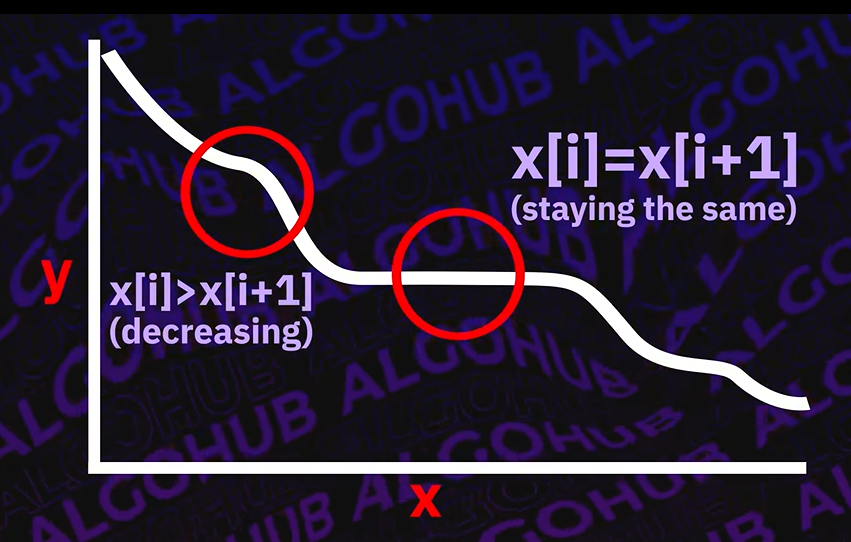
Next Greater Element
단조 스택이 사용되는 대표적인 예시는 Next Greater Element를 찾는 문제이다.
아래 그림은 자신의 오른쪽에서 자신보다 값이 큰 원소 (Next Greater Element) 를 찾아 해당 원소의 번호를 출력한 것이다.
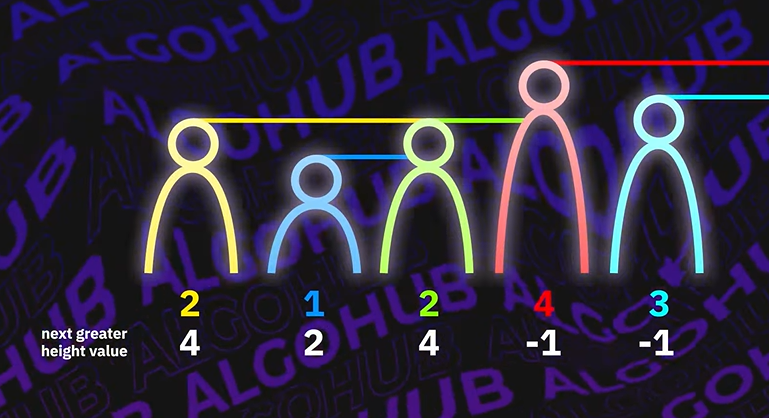
가장 기본적인 브루트포스 방법으로 풀면, 각 원소에 대해 자신의 오른쪽에 있는 모든 원소를 탐색해야 하므로 시간 복잡도가 O(N^2)이 나온다. 여기서, 단조 감소 스택을 이용하여 시간 복잡도를 O(N)으로 줄일 수 있다!
입력 배열 [2, 1, 2, 4, 3] 의 오른쪽에서 왼쪽으로 이동하며 각 원소에 대한 Next Greater Element를 찾아보자.

원소 3의 오른쪽에는 아무것도 없고, 스택도 비어있기 때문에, 3을 스택에 넣고 정답 배열에는 -1을 저장한다.
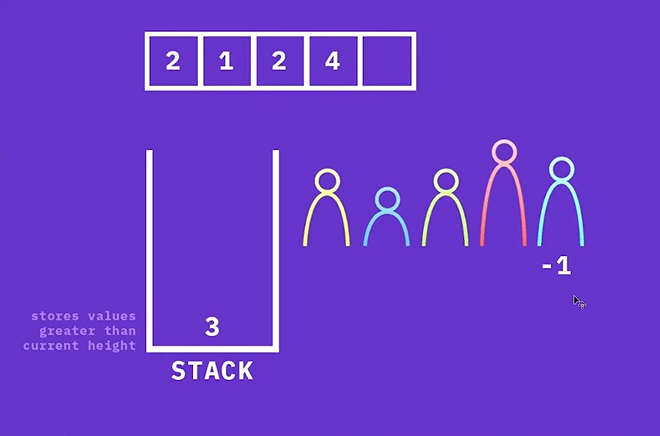
다음으로 원소 4의 오른쪽에는 자신보다 큰 값이 없다.
단조 '감소' 스택이므로 3을 pop 했는데, 스택의 top에 4보다 큰 값이 없다. (스택이 비어있다.)
따라서, 4의 정답 배열에는 -1을 저장하고 4를 스택에 push 한다.
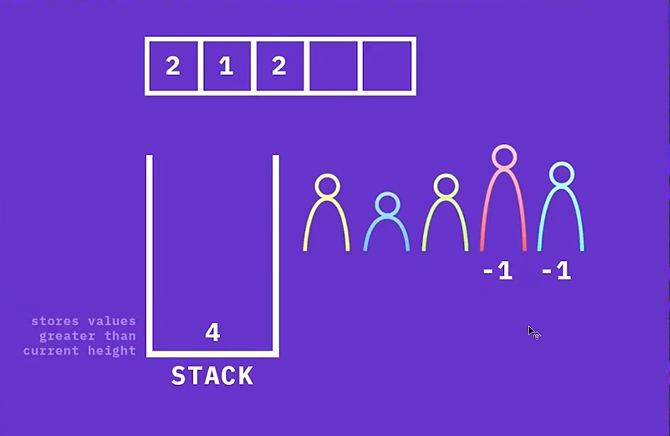
다음으로 원소 2의 Next Greater Element는 4이다.
단조 감소 스택의 top에 원소 2보다 큰 값이 저장되어 있고, 해당 값을 정답 배열에 저장한다.
그리고 원소 2는 top에 있는 4보다 작기 때문에 스택에 그대로 push 한다.
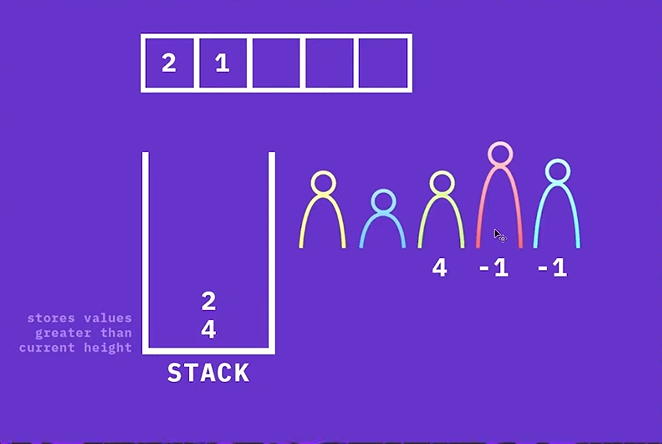
다음으로 원소 1의 Next Greater Element는 2이다.
단조 감소 스택의 top에 원소 1보다 큰 값이 저장되어 있고, 해당 값을 정답 배열에 저장한다.
그리고 원소 1은 top에 있는 2보다 작기 때문에 스택에 그대로 push 한다.
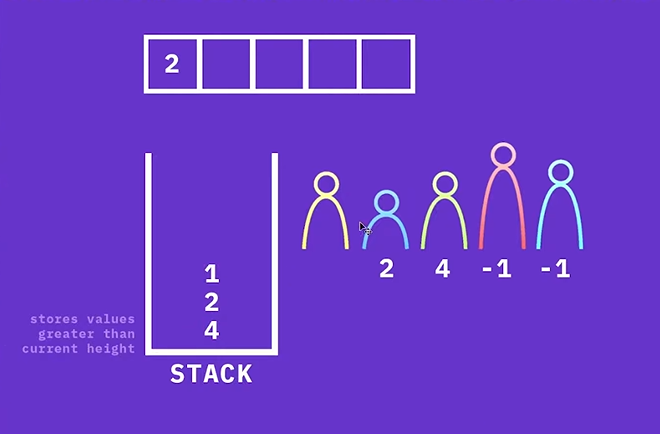
마지막으로 원소 2는 top에 있는 원소보다 크기 때문에 스택에 push 할 수 없다. 따라서, 원소 2보다 큰 값이 나올 때까지 스택의 원소를 pop 한다.
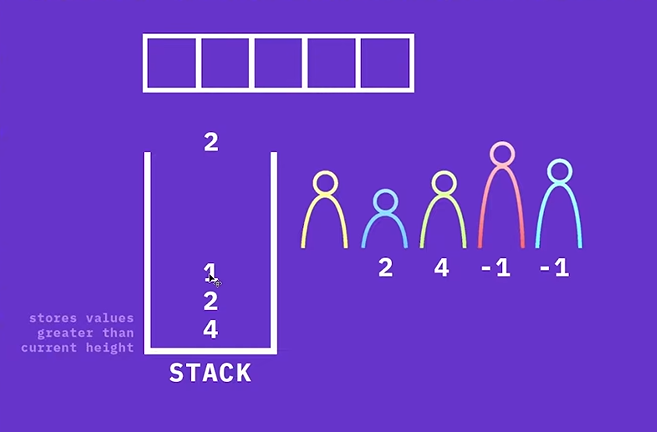
스택의 top에 있는 4가 원소 2의 Next Greater Element가 된다.
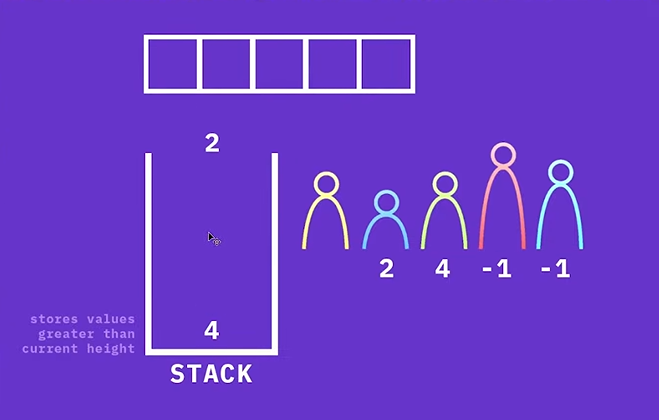
이렇게 해서, Next Greater Element를 모두 구했다!
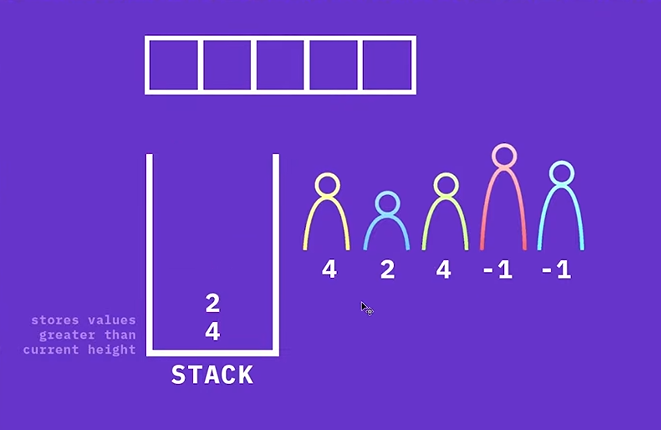
C++ 코드로 구현
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
vector<int> nextGreaterElement(vector<int> heights) {
int n = heights.size();
vector<int> ans(n, 0);
stack<int> st;
for(int i = n - 1; i >= 0; i--){
// 현재 값보다 스택의 top이 더 클 때까지 pop
while(!st.empty() && st.top() <= heights[i]){
st.pop();
}
// 현재 값보다 큰 값이 스택에 없으므로 -1
if(st.empty()) ans[i] = -1;
// Next Greater Element 발견
else ans[i] = st.top();
// 현재 값을 스택에 push
st.push(heights[i]);
}
return ans;
}
int main(void) {
ios::sync_with_stdio(0);
cin.tie(0);
vector<int> heights = {2, 1, 2, 4, 3};
vector<int> ans = nextGreaterElement(heights);
// 4 2 4 -1 -1
for(auto e: ans){
cout << e << " ";
}
return 0;
}시간 복잡도
위 코드의 시간 복잡도는 O(N)이다. 이중 루프니까 O(N^2) 아닌가? 라고 생각할 수 있지만, 그렇지 않다!!
그래서 단조 스택이 브루트포스 보다 시간 복잡도를 낮출 수 있는 유용한 방법이 되는 것이다!
위의 코드에서 while 루프는 스택 원소를 pop 하면서 모든 원소를 한번씩 push 하기 때문에, 스택에 푸시되는 원소는 N개 이상이 될 수 없다.
내부 루프는 N개의 요소를 포함할 때까지 중첩 루프로 계산되지 않으므로, 결국 시간복잡도는 O(N)이 된다.
2493번 문제
위의 문제와 유사하게 이 문제를 해결할 수 있다. 다만, 이 문제는 Next Greater Element의 값이 아니라 '인덱스'를 구해야 하므로, stack에 인덱스와 값을 같이 묶어서 저장한다.
그리고 오른쪽이 아니라, '왼쪽'에 있는 원소들 중에서 자신보다 큰 값을 찾아야 한다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <stack>
#include <set>
using namespace std;
const int MAX = 500001;
int height[MAX];
int answer[MAX];
int main(void) {
ios::sync_with_stdio(0);
cin.tie(0);
int N;
cin >> N;
for(int i = 0; i < N; i++){
cin >> height[i];
}
stack<pair<int, int>> st;
// 오른쪽에서 왼쪽으로 이동
for(int i = N - 1; i >= 0; i--){
// 스택에 넣으려는 값(왼쪽)과 기존에 스택의 top에 있는 값(오른쪽) 비교
while(!st.empty() && st.top().second < height[i]){
// 새로운 값(왼쪽)이 더 크면 해당 탑의 번호 저장
answer[st.top().first] = i + 1;
st.pop();
}
st.push({i, height[i]});
}
for(int i = 0; i < N; i++){
cout << answer[i] << " ";
}
return 0;
}


