우선, C++ STL을 사용하지 않고 재귀 함수로 순열과 조합을 구현해보자!
조합
조합은 서로 다른 n개의 원소 중에 중복을 허용하지 않고 r개를 뽑는 경우의 수를 말한다. 조합은 원소를 뽑기만 하고 그들의 순서는 고려하지 않는다.
예를 들어, 아래와 같은 5개의 원소 중에 3개를 뽑는 경우의 수를 생각해보자.
(1, 2, 3, 4, 5)
(1, 2, 3) (1, 2, 4) (1, 2, 5) ... (3, 4, 5) → 10가지
여기서 중요한 점은, 조합은 한번 뽑은 원소는 다시 뽑지 않는다는 것이다!
일단 1을 시작점으로 잡아보자.
(1, 2, 3) (1, 2, 4) (1, 2, 5) (1, 3, 4) (1, 3, 5) (1, 4, 5)
2를 시작점으로 하면,
(2, 1, 3) (2, 1, 4) (2, 1, 5) (2, 3, 4) (2, 3, 5) (2, 4, 5)
그런데, 1이 포함된 앞의 세 가지 경우의 수는 1을 시작점으로 했을 때 이미 구했다! 왜냐하면, 조합은 순서를 고려하지 않기 때문이다!
따라서, 조합을 구현할 때 하나의 시작점을 정한다면, 그 시작점 이전에 나온 원소들은 다시 뽑지 않는다는 걸 반드시 기억하고 아래 코드를 보자!
#include <iostream>
#define MAX 8
using namespace std;
int n, r;
int arr[MAX]; // 0으로 초기화
bool selected[MAX]; // false로 초기화
void printArray(){
for(int i = 0; i < n; i++){
if(selected[i]){
cout << arr[i] << " ";
}
}
cout << "\n";
}
void dfs(int idx, int cnt){ // 시작 인덱스, 뽑은 개수
if(cnt == r){ // r개의 원소를 모두 뽑았는지 검사
printArray();
return;
}
// idx 이전의 원소는 이미 선택했으니까 그 이후의 원소들 중에서 뽑는다.
for(int i = idx; i < n; i++){
if(!selected[i]){
selected[i] = true;
dfs(i, cnt + 1);
selected[i] = false;
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> r;
for(int i = 0; i < n; i++){
arr[i] = i + 1;
}
dfs(0, 0);
return 0;
}5 3
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
여기서 핵심은 dfs(int idx, int cnt) 함수이다!
arr 배열은 입력값을 저장하는 배열이며, selected 배열은 이미 선택한 원소라면 선택하지 않고, 선택하지 않은 원소라면 선택하는 배열이다. 즉, selected 배열을 통해 중복을 허용하지 않도록 만들 수 있다! (미리 스포하자면, 중복조합과 중복순열에서는 selected 배열이 사용되지 않는다.)
다음으로, dfs 함수의 매개변수를 살펴보자. idx는 시작점을 결정하는 변수이며, cnt는 우리가 원하는 개수만큼 뽑았는지 판단하는 변수이다.
void dfs(int idx, int cnt){
if(cnt == r){ // r개의 원소를 모두 뽑았는지 검사
printArray();
return;
}
// idx 이전의 원소는 이미 선택했으니까 그 이후의 원소들 중에서 뽑는다.
for(int i = idx; i < n; i++){
if(!selected[i]){
selected[i] = true;
dfs(i, cnt + 1); // 이 부분이 핵심!!!!!
selected[i] = false;
}
}
}for문을 보면, i번째 원소를 이미 선택했다면 그냥 지나가고, 선택하지 않았다면 선택했다고 표시한 뒤에 dfs(i, cnt + 1) 함수를 통해 재귀 호출한다.
메인 함수에서 dfs(0, 0)를 호출하면 어떤 일이 일어나는지 살펴보자.
| idx | cnt | 알고리즘 |
|---|---|---|
| 0 | 0 | - 0번은 선택하지 않았으니까 선택 - dfs(0, 1) 재귀 호출 |
| 0 | 1 | - 0번은 선택했으니까 pass - 1번은 선택하지 않았으니까 선택 - dfs(1, 2) 재귀 호출 |
| 1 | 2 | - 1번은 선택했으니까 pass - 2번은 선택하지 않았으니까 선택 - dfs(2, 3) 재귀 호출 |
| 2 | 3 | - cnt가 3이 되었으니 원하는 작업을 진행하고 return |
현재 0, 1, 2번 원소가 선택되었으므로 (1, 2, 3)이 출력될 것이다.
그리고 나서 return을 하면 어떻게 될까? (idx=2, cnt=3)에서 (idx=1, cnt=2)로 들어가게 될 것이다.
이 함수에 남아있는 작업이 있다! 2번째 원소를 선택하고 재귀 호출한 뒤에 2번째 값을 선택하지 않은 것으로 다시 표시하는 것이다. 이후 for문이 계속 실행될 것이다.
| idx | cnt | 알고리즘 |
|---|---|---|
| 0 | 0 | - 0번은 선택하지 않았으니까 선택 - dfs(0, 1) 재귀 호출 |
| 0 | 1 | - 0번은 선택했으니까 pass - 1번은 선택하지 않았으니까 선택 - dfs(1, 2) 재귀 호출 |
| 1 | 2 | - 1번은 선택했으니까 pass - 2번은 선택하지 않았으니까 선택 - dfs(2, 3) 재귀 호출 (여기로 돌아옴 ⭐) - 2을 선택하지 않은 것으로 표시 - i++되어 i = 3 - 3번은 선택하지 않았으니까 선택 - dfs(3, 3) 재귀 호출 |
| 3 | 3 | cnt가 3이 되었으니 원하는 작업을 진행하고 return |
이번에는 2번 선택이 취소되고 0, 1, 3번이 선택되었으므로 (1, 2, 4)가 출력될 것이다!!! 이런 식으로 조합에 대한 모든 경우의 수를 구할 수 있다!!!
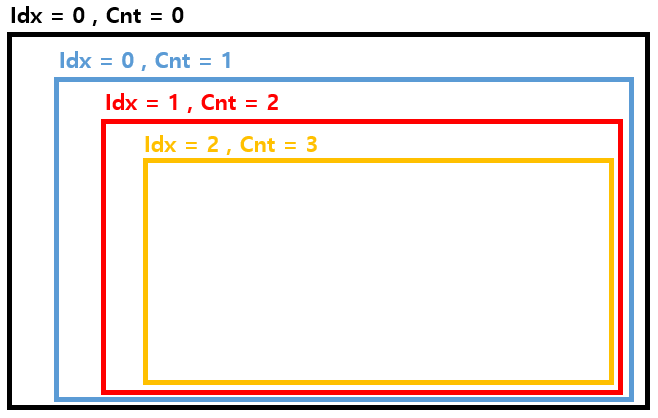
👉 (idx = 2, cnt = 3)에서 리턴하면 (idx = 1, cnt = 2)로 돌아간다.
백트래킹
void dfs(int cnt, int idx) { // 현재까지의 결과, 탐색을 진행할 인덱스
// r개를 선택한 경우
if(cnt == r) {
// 결과 처리 후 현재 가지에 대한 탐색 종료
return;
}
// r개를 선택하지 않은 경우 재귀 호출 반복
for(int i = idx; i < n; i++){
if(!selected[i]){
selected[i] = true; // 상태 변화
dfs(cnt + 1, i); // 재귀 호출
selected[i] = false; // 다음 경우의 수를 위해 상태 복구
}
}
}👉 DFS로 깊이 있게 들어가다가 r개를 모두 선택하면 현재 가지에 대한 탐색을 종료한다. 그리고 다음 경우의 수에 대한 탐색을 위해 상태를 복구하고 다시 재귀 호출을 반복한다. 이런 점에서 조합은 백트래킹의 예시라고 볼 수 있다.
순열
순열은 서로 다른 n개의 원소 중에서 중복을 허용하지 않고 r개를 선택하여 나열하는 경우의 수를 말한다. 조합과 달리, 순열은 순서를 고려한다는 게 중요하다!
조합은 과거에 시작점으로 삼았던 원소는 다시 쳐다도 보지 않는다고 했다. 하지만, 순열은 과거에 시작점으로 삼았던 원소를 다시 쳐다봐야 한다! 왜냐하면, 순열은 순서가 달라지면 다른 경우의 수로 취급하기 때문이다.
#include <iostream>
#include <vector>
#define MAX 8
using namespace std;
int n, r;
int arr[MAX]; // 0으로 초기화
bool selected[MAX]; // false로 초기화
vector<int> v;
void printArray(){
for(int i = 0; i < v.size(); i++){
cout << v[i] << " ";
}
cout << "\n";
}
void dfs(int cnt){
if(cnt == r){
printArray();
return;
}
for(int i = 0; i < n; i++){
if(!selected[i]){ // 가지치기 (백트래킹)
selected[i] = true; // 상태 변화
v.push_back(arr[i]);
dfs(cnt + 1); // 재귀 호출
v.pop_back(); // 상태 복구
selected[i] = false;
}
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> r;
for(int i = 0; i < n; i++){
arr[i] = i + 1;
}
dfs(0);
return 0;
}3 2
1 2
1 3
2 1
2 3
3 1
3 2
조합과 다른 점을 유의 깊게 살펴보자. 순열은 시작점을 다시 한번 쳐다봐야 하기 때문에 dfs 함수에 idx라는 매개변수가 없어도 된다. 그리고 조합은 selected[i] = true인 원소만 출력하면 되지만, 순열은 이게 불가능하다.
순열에서 처음에 (1, 2, 3)을 출력하고, 그 다음으로 (2, 1, 3)을 선택하면 이는 (1, 2, 3)과 다른 경우이므로 출력이 될텐데, selected[i] = true를 기준으로 출력하면, (1, 2, 3)이 또 출력되기 때문이다. 따라서 원소를 선택할 때마다 벡터에 넣었다가 빼는 방식으로 출력하는 것이다.
중복 조합
서로 다른 n개의 원소 중에서 r개를 선택하는데 중복을 허용하면 중복조합이다. selected 배열은 이전에 조합에서 사용했던 목적과 다르게 사용된다. 아래 코드를 보자.
#include <iostream>
#define MAX 8
using namespace std;
int n, r;
int arr[MAX]; // 0으로 초기화
int selected[MAX]; // 0으로 초기화
void dfs(int idx, int cnt){
if(cnt == r){
for(int i = 0; i < r; i++){
cout << selected[i] << " ";
}
cout << "\n";
return;
}
for(int i = idx; i < n; i++){
// cnt번째로 선택된 카드를 arr[i]로 지정
selected[cnt] = arr[i];
dfs(i, cnt + 1);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> r;
for(int i = 0; i < n; i++){
arr[i] = i + 1;
}
dfs(0, 0);
return 0;
}4 2
1 1
1 2
1 3
1 4
2 2
2 3
2 4
3 3
3 4
4 4
중복조합은 선택했던 카드를 다시 선택할 수 있으므로, selected 배열을 bool형으로 사용하지 않는다. 결국 selected[cnt] = arr[i]라는 말은 cnt번째로 선택한 카드가 arr[i]라는 것을 의미한다. 그래서 이번에는 selected 배열이 int형으로 선언되었음에 유의하자.
중복 순열
서로 다른 n개 중에서 r개를 선택하여 나열하는데, 중복이 허용되면 중복 순열이다.
#include <iostream>
#define MAX 8
using namespace std;
int n, r;
int arr[MAX]; // 0으로 초기화
int selected[MAX]; // 0으로 초기화
void dfs(int cnt){
if(cnt == r){
for(int i = 0; i < r; i++){
cout << selected[i] << " ";
}
cout << "\n";
return;
}
for(int i = 0; i < n; i++){
// cnt번째로 선택된 카드를 arr[i]로 지정
selected[cnt] = arr[i];
dfs(cnt + 1);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> r;
for(int i = 0; i < n; i++){
arr[i] = i + 1;
}
dfs(0);
return 0;
}4 2
1 1
1 2
1 3
1 4
2 1
2 2
2 3
2 4
3 1
3 2
3 3
3 4
4 1
4 2
4 3
4 4
중복조합에서와 마찬가지로, selected 배열은 해당 인덱스의 원소가 이미 선택된 것인지 아닌지를 판단하기 위한 것이 아니라, 선택된 원소의 값을 저장하는 역할을 하고 있다. 그래서 int형이다. 또한 순열 코드와 마찬가지로 dfs 함수의 매개변수는 cnt 하나만 필요하다!
관련 문제 풀기
순열: N과 M (1)
https://www.acmicpc.net/problem/15649
#include <iostream>
#define MAX 9
using namespace std;
int n, m;
int arr[MAX];
bool selected[MAX];
// 선택된 m개를 출력한다.
void printArray(){
for(int i = 0; i < m; i++){
cout << arr[i] << " ";
}
cout << "\n";
}
void dfs(int cnt){ // 뽑은 개수
if(cnt == m){
printArray();
return;
}
for(int i = 1; i <= n; i++){ // 1부터 시작
if(!selected[i]){
selected[i] = true;
arr[cnt] = i; // 선택된 값을 저장한다.
dfs(cnt + 1);
selected[i] = false;
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
dfs(0);
return 0;
}조합: N과 M (2)
https://www.acmicpc.net/problem/15650
#include <iostream>
#define MAX 9
using namespace std;
int n, m;
int arr[MAX];
bool selected[MAX];
// 선택된 m개를 출력한다.
void printArray(){
for(int i = 0; i < m; i++){
cout << arr[i] << " ";
}
cout << "\n";
}
void dfs(int num, int cnt){ // 숫자 번호, 뽑은 개수
if(cnt == m){
printArray();
return;
}
for(int i = num; i <= n; i++){ // num부터 시작
if(!selected[i]){
selected[i] = true;
arr[cnt] = i; // 선택된 값을 저장한다.
dfs(i, cnt + 1);
selected[i] = false;
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
dfs(1, 0);
return 0;
}중복 순열: N과 M (3)
https://www.acmicpc.net/problem/15651
#include <iostream>
#define MAX 9
using namespace std;
int n, m;
int arr[MAX];
// 선택된 m개를 출력한다.
void printArray(){
for(int i = 0; i < m; i++){
cout << arr[i] << " ";
}
cout << "\n";
}
void dfs(int cnt){ // 뽑은 개수
if(cnt == m){
printArray();
return;
}
for(int i = 1; i <= n; i++){ // 1부터 시작
arr[cnt] = i; // 선택된 값을 저장한다.
dfs(cnt + 1);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
dfs(0);
return 0;
}중복 조합: N과 M (4)
https://www.acmicpc.net/problem/15652
#include <iostream>
#define MAX 9
using namespace std;
int n, m;
int arr[MAX];
// 선택된 m개를 출력한다.
void printArray(){
for(int i = 0; i < m; i++){
cout << arr[i] << " ";
}
cout << "\n";
}
void dfs(int num, int cnt){ // 숫자 번호, 뽑은 개수
if(cnt == m){
printArray();
return;
}
for(int i = num; i <= n; i++){
arr[cnt] = i; // 선택된 값을 저장한다.
dfs(i, cnt + 1);
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
dfs(1, 0);
return 0;
}C++ STL 사용하기
순열
next_permutation
주어진 수열에 대해 사전 순으로 다음 순열이 무엇인지 구할 때 사용하는 함수 (다음 순열이 존재하면 true, 아니면 false 반환)
do-while문과 같이 사용하면 가능한 모든 순열을 구할 수 있다.
단, 주의할 점은 초기에 주어진 수열이 오름차순으로 정렬되어 있지 않으면, 해당 수열을 기준으로 그 다음 순열만 구하기 때문에 가능한 모든 순열을 구할 수 없다.
따라서, 오름차순으로 정렬된 배열이어야 모든 경우의 수를 구할 수 있다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, r;
cin >> n >> r;
vector<int> v;
for(int i = 0; i < n; i++){
v.push_back(i + 1); // 오름차순
}
do{
for(int i = 0; i < n; i++)
cout << v[i] << " ";
cout << "\n";
}while(next_permutation(v.begin(), v.end()));
return 0;
}3 2
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
prev_permutation
주어진 수열에 대해 사전 순으로 이전 순열이 무엇인지 구할 때 사용하는 함수 (이전 순열이 존재하면 true, 아니면 false 반환)
아까와는 반대로 내림차순 정렬된 배열이어야 가능한 이전 순열을 모두 구할 수 있다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, r;
cin >> n >> r;
vector<int> v;
for(int i = n; i >= 1; i--){
v.push_back(i); // 내림차순
}
do{
for(int i = 0; i < n; i++)
cout << v[i] << " ";
cout << "\n";
}while(prev_permutation(v.begin(), v.end()));
return 0;
}3 2
3 2 1
3 1 2
2 3 1
2 1 3
1 3 2
1 2 3
조합
next_permutation
조합은 순서를 고려하지 않기 때문에 next_permutation 함수를 그대로 사용하면 안 된다.
예를 들어 (1, 2), (2, 1)은 순열에서는 다른 경우지만, 조합에서는 같은 경우로 취급하기 때문이다.
이러한 중복을 피하기 위한 별도 처리가 필요한데, 0과 1로만 구성된 보조적인 수열을 이용하면 된다. 방법은 다음과 같다.
- 0 -> 1 순으로 구성된 오름차순 보조 수열을 정의한다. 즉, 앞의 (n-r)개는 0으로, 나머지 r개는 1로 초기화 한다.
- 해당 보조 수열로 next_permutation 함수를 수행한다.
- 그때마다 변하는 보조 순열을 순회하면서, 값이 1인 경우에만 원래 배열의 원소로 대체하여 출력한다.
예를 들어 (1, 2, 3, 4, 5)으로 구성된 수열에서 3개를 선택하는 조합의 경우, 보조 수열이 (0, 0, 1, 1, 1)이 될 것이다.
(0, 0, 1, 1, 1)에 대해 next_permutation() 함수를 돌리면, 가능한 경우의 수는 5!이 아니라, 5!/(2! * 3!)이 된다.
그리고 보조 수열의 값이 1일 때는, 해당 인덱스에 대응하는 원래 배열의 원소 값으로 대체하여 출력하면 된다.
(0, 0, 1, 1, 1) -> (3, 4, 5)
(0, 1, 0, 1, 1) -> (2, 4, 5)
...
(1, 1, 1, 0, 0) -> (1, 2, 3)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n, r;
cin >> n >> r;
vector<int> arr(n);
for(int i = 0; i < n; i++){
arr[i] = i + 1;
}
// 0 -> 1 순으로 구성된 오름차순 보조 배열
vector<int> select(arr.size(), 1);
for(int i = 0; i < n - r; i++){
select[i] = 0;
}
do{
for(int i = 0; i < arr.size(); i++){
if(select[i]) {
cout << arr[i] << " ";
}
}
cout << "\n";
// 다음 순열이 존재하면 true 반환
}while(next_permutation(select.begin(), select.end()));
return 0;
}5 3
3 4 5
2 4 5
2 3 5
2 3 4
1 4 5
1 3 5
1 3 4
1 2 5
1 2 4
1 2 3
prev_permutation
이번에는 1 -> 0 순으로 구성된 내림차순 보조 배열을 이용하면 된다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
int n, r;
cin >> n >> r;
vector<int> arr(n);
for(int i = 0; i < n; i++){
arr[i] = i + 1;
}
// 1 -> 0 순으로 구성된 내림차순 보조 배열
vector<int> select(arr.size(), 0);
for(int i = 0; i < r; i++){
select[i] = 1;
}
do{
for(int i = 0; i < arr.size(); i++){
if(select[i]) {
cout << arr[i] << " ";
}
}
cout << "\n";
// 이전 순열이 존재하면 true 반환
}while(prev_permutation(select.begin(), select.end()));
return 0;
}5 3
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

