출처: https://ip99202.github.io/posts/%EC%9C%A0%EB%8B%88%EC%98%A8-%ED%8C%8C%EC%9D%B8%EB%93%9C(Union-Find)/
유니온 파인드란?
- 대표적인 그래프 알고리즘으로, 두 노드가 같은 집합에 속하는지 판별하는 알고리즘이다.
- 합집합 찾기 알고리즘이라고도 부르며, 반대로 서로 연결되어 있지 않은 노드를 판별할 수도 있기 때문에 서로소 집합 (Disjoint-set)이라고도 부른다.
- 노드를 합치는 Union 연산과 노드의 루트 노드를 찾는 Find 연산으로 이루어진다.
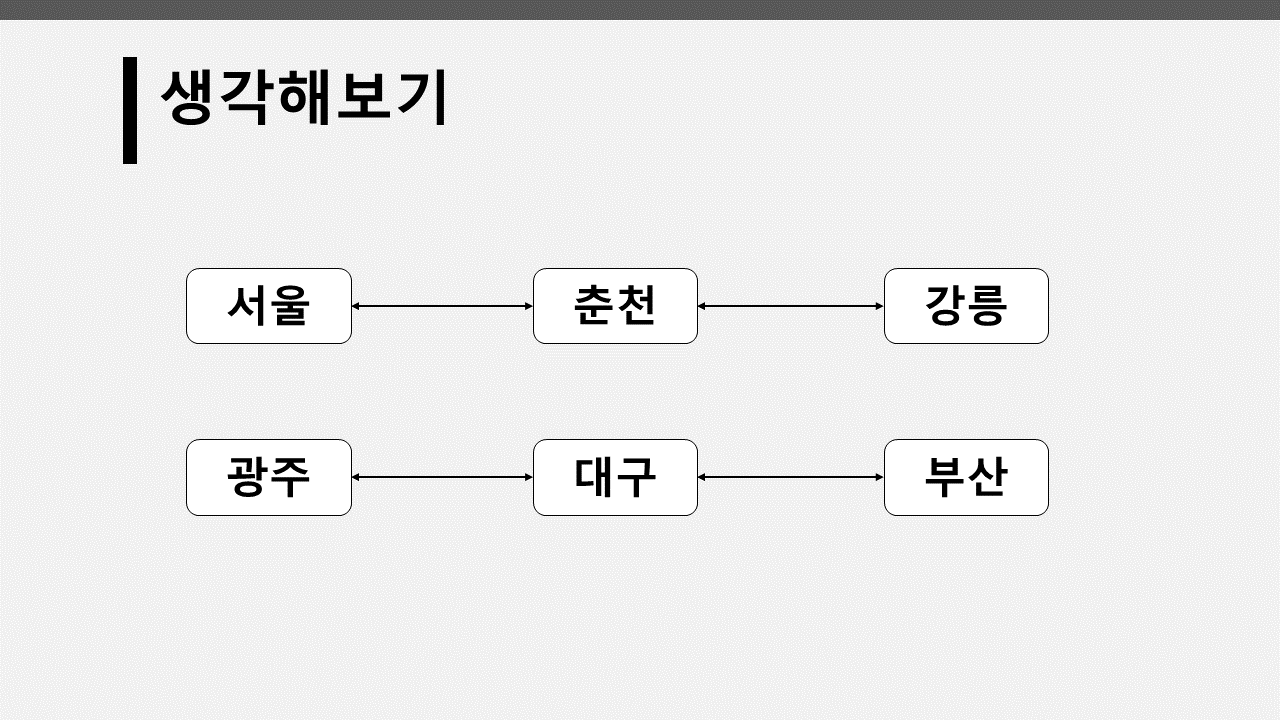
이렇게 생긴 기차 노선이 있다고 할 때, 기차를 타고 서울에서 강릉으로 가는 것은 가능하지만 서울에서 부산으로 가는 건 불가능하다. 이처럼 간단한 그래프에서는 한 노드에서 다른 노드로 가는 길이 이어져 있는지 판단하는 게 쉽다.
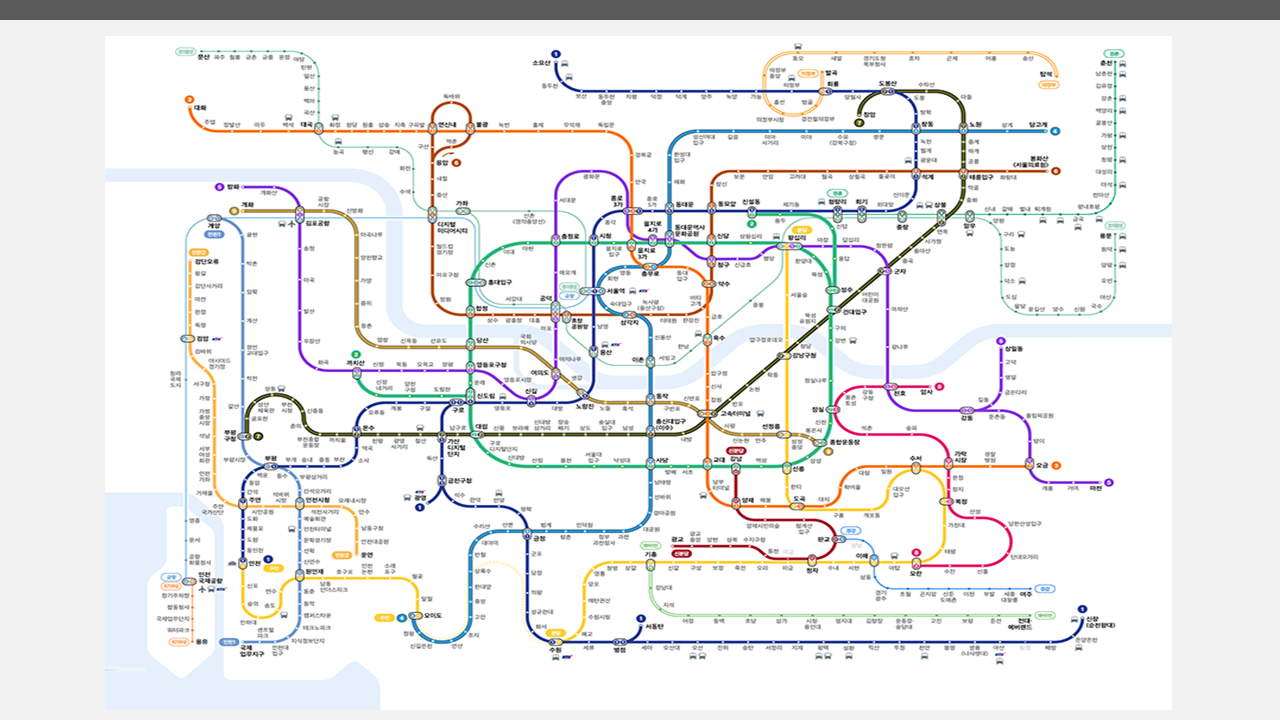
그런데, 이렇게 복잡한 그래프에서는 빠른 시간 안에 두 노드가 연결되어 있는지 판별하는 게 힘들다. 이러한 그래프에서도 두 노드가 연결되어 있는지, 끊어져 있는지 빠르게 판별하려면 알고리즘을 어떻게 짜야 할까?
알고리즘 이해
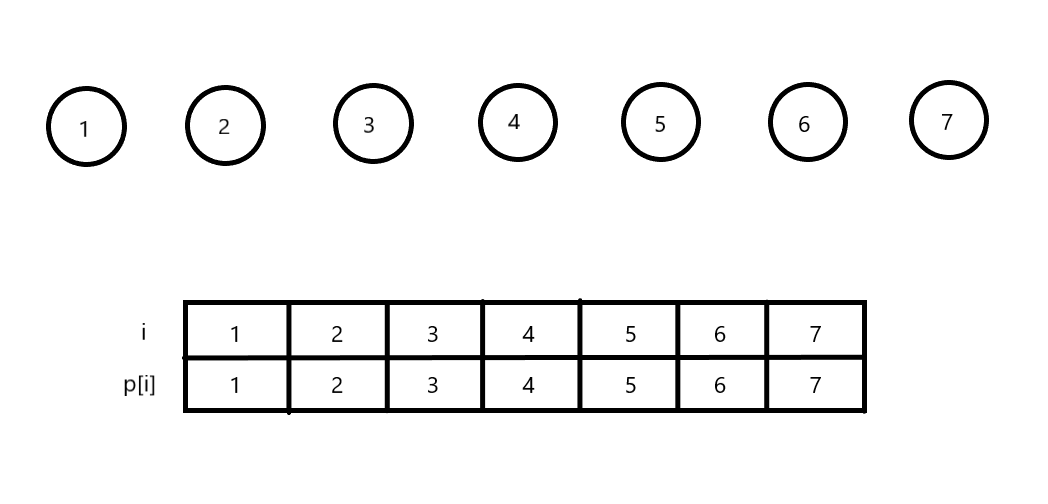
7개의 단절된 노드가 있다. 위의 표는 부모 노드의 번호를 저장하는 배열을 나타낸 것이다. 현재 모든 노드가 단절되어 있기 때문에 배열의 값은 자기 자신의 번호이다.
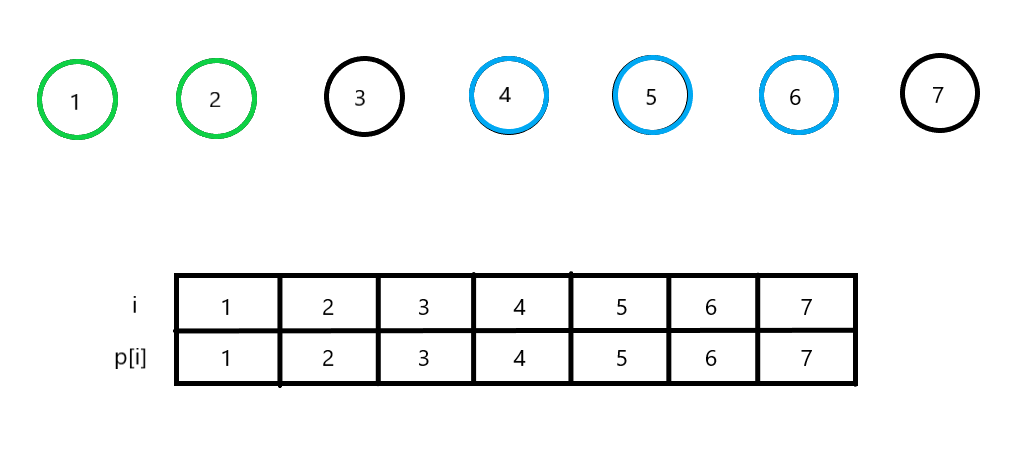
이 중에서 1 2 노드와 4 5 6 노드를 연결하고 싶다.
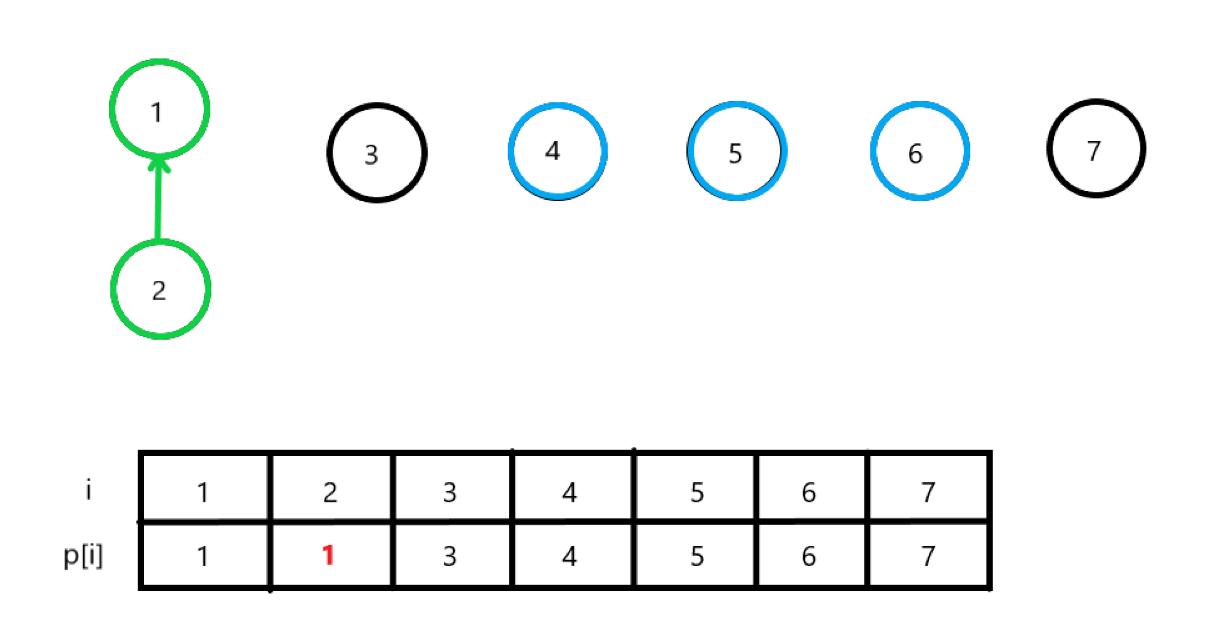
우선 1 2 노드를 합쳐보았다. 이 상태를 배열의 값에 반영하려면 어떻게 해야 될까? 바로 2번 노드의 배열 값을 1번 노드의 배열 값으로 바꿔주면 된다. 즉, 1번은 2번의 부모 노드가 되는 것이다.
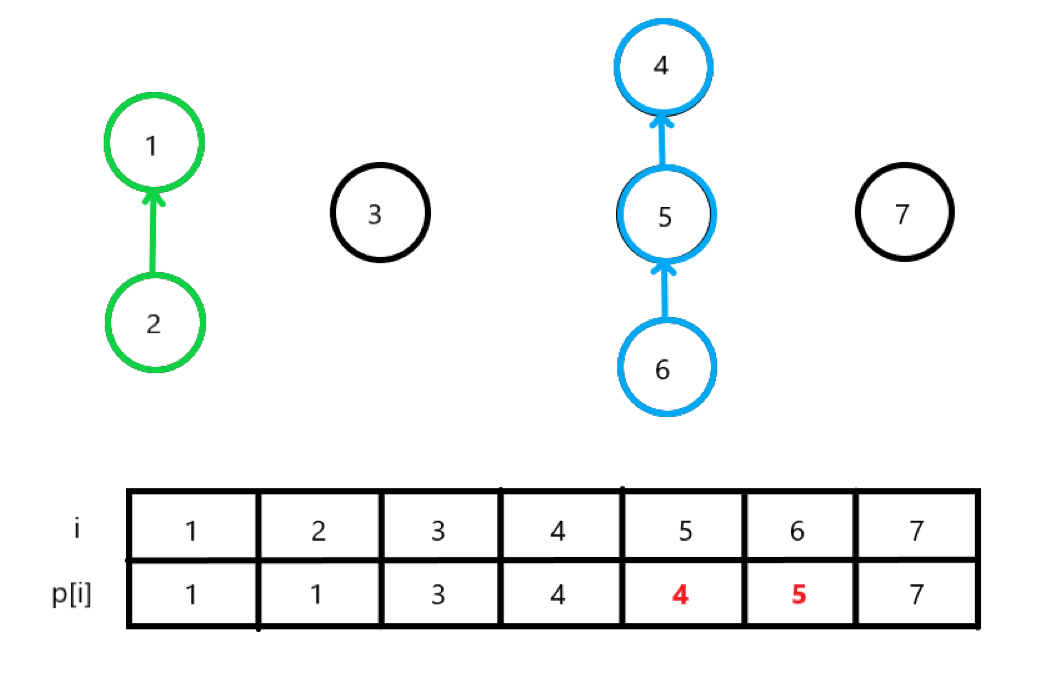
4 5 6 노드도 마찬가지 방식으로 합쳐주었다.
이제 이 상태에서 2번과 6번 노드가 서로 연결되어 있는지 확인하려면, 각 노드의 루트 노드가 동일한지 확인하면 된다.
2번 노드가 속해있는 트리의 루트 노드를 찾는 과정
- 배열의 2번에 있는 값을 확인한다. 1번이다.
- 배열의 1번에 있는 값을 확인한다. 1번이다.
- 배열의 인덱스와 값이 일치한다.
- 그렇다면 1번 노드가 2번 노드가 속해있는 트리의 루트 노드이다.
6번 노드가 속해있는 트리의 루트 노드를 찾는 과정
- 배열의 6번에 있는 값을 확인한다. 5번이다.
- 배열의 5번에 있는 값을 확인한다. 4번이다.
- 배열의 4번에 있는 값을 확인한다. 4번이다.
- 배열의 인덱스와 값이 일치한다.
- 그렇다면 4번 노드가 6번 노드가 속해있는 트리의 루트 노드이다.
이제 2번과 6번 노드의 루트를 각각 확인했을 때 서로 다르다면, 두 노드는 연결되어 있지 않은 것이다. 그런데 이 방법의 문제점이 하나 있다.
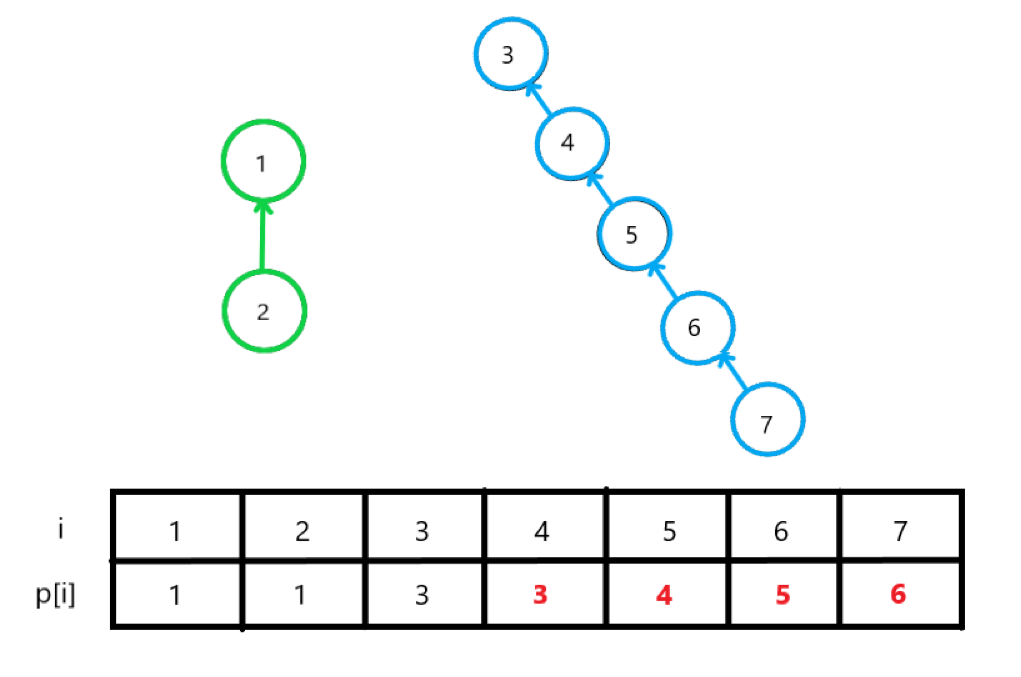
이처럼 트리에서 한쪽으로만 노드가 치우칠 경우, Find 연산에서 재귀 호출을 통해 루트 노드를 찾을 때 탐색 시간이 오래 걸린다. 이 문제를 해결하려면 두 노드를 합치는 Union 연산을 할 때, 단순히 인접한 부모 노드의 번호가 아니라 '루트 노드의 번호'를 저장해야 한다.
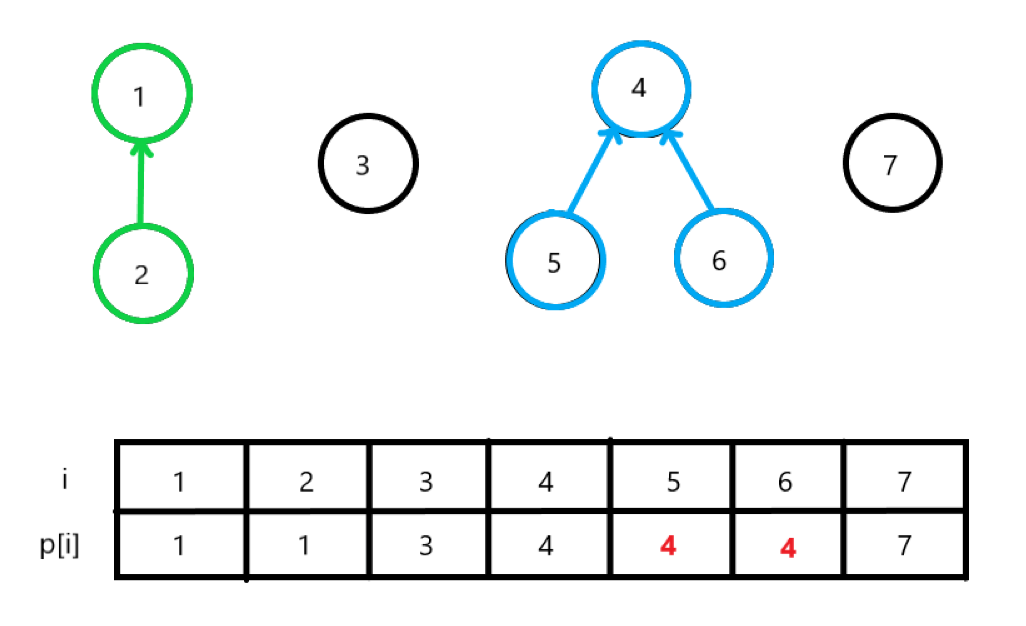
이렇게 6번 노드의 값을 5번(부모 노드)이 아니라 4번(루트 노드)으로 저장하면, 결과적으로 위와 같은 트리가 형성된다. 이러한 방식으로 번호를 저장하면, 트리의 치우침 문제를 해결할 수 있다.
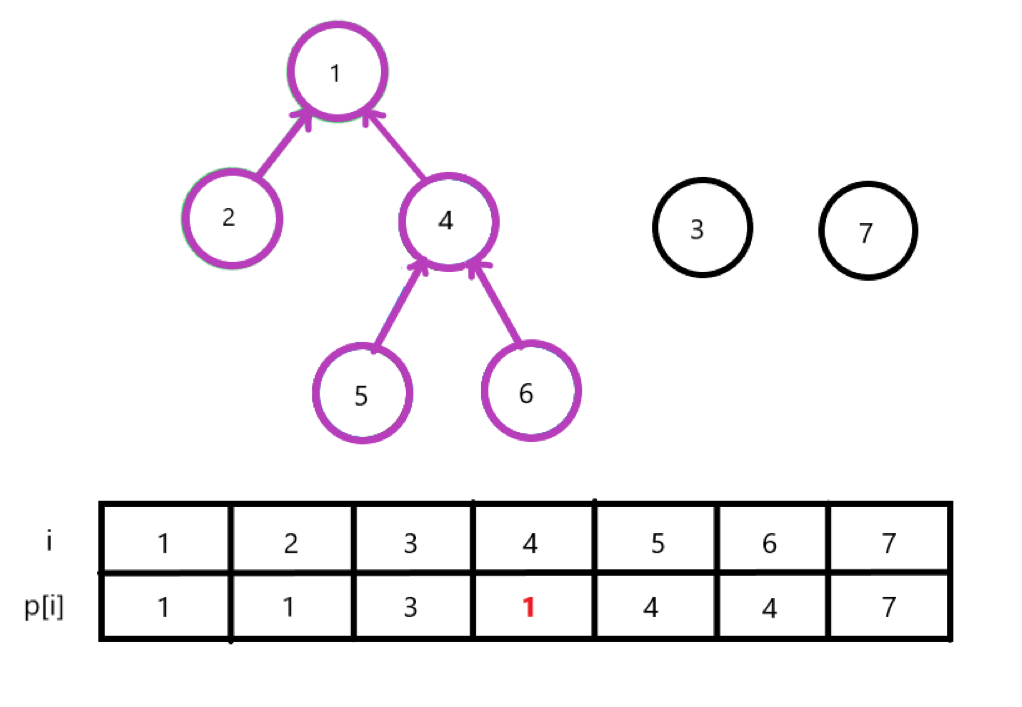
1번과 4번 노드를 연결한다면 위와 같은 모양의 트리가 만들어질 것이다.
코드로 구현
#include <iostream>
using namespace std;
// 각 정점의 부모 노드 번호를 저장하는 배열 (최종적으로는 루트 노드 번호)
int parent[8];
// 루트 노드를 찾는 Find 연산
int Find(int x) {
// 배열의 인덱스와 값이 같다면 루트 노드 발견!
if (x == parent[x]) return x;
// 부모 노드의 번호를 전달하면서, 루트 노드를 찾을 때까지 재귀 호출 반복
return parent[x] = Find(parent[x]);
}
// 두 노드를 같은 집합으로 합치는 Union 연산
void Union(int x, int y) {
x = Find(x);
y = Find(y);
// 루트 노드가 같다면 이미 연결되어 있는 것
if (x == y) return;
// 더 작은 값이 부모 노드가 될 수 있도록
if (x < y) parent[y] = x;
else parent[x] = y;
}
// 두 노드가 연결되어 있는지 판별하는 함수
bool isUnion(int x, int y) {
x = Find(x);
y = Find(y);
// 루트 노드가 같은지 확인
return (x == y);
}
int main() {
for (int i = 1; i <= 7; i++)
parent[i] = i;
Union(1, 2); // p[2] = 1
Union(4, 5); // p[5] = 4
Union(5, 6); // p[6] = 4 (5번이 아니라 4번 저장)
cout << "2와 4는 같은 집합인가? " << isUnion(2, 4) << "\n"; // false
Union(1, 4); // p[4] = 1
cout << "2와 4는 같은 집합인가? " << isUnion(2, 4) << "\n"; // true
return 0;
}위와 같은 코드로 트리의 치우침 문제가 해결되는지 직접 확인해보자!

#include <iostream>
using namespace std;
int parent[8];
// 루트 노드를 찾는 Find 연산
int Find(int x) {
if (x == parent[x]) return x;
return parent[x] = Find(parent[x]);
}
// 두 노드를 같은 집합으로 합치는 Union 연산
void Union(int x, int y) {
x = Find(x);
y = Find(y);
if (x == y) return;
if (x < y) parent[y] = x;
else parent[x] = y;
}
// 두 노드가 연결되어 있는지 판별하는 함수
bool isUnion(int x, int y) {
x = Find(x);
y = Find(y);
return (x == y);
}
int main() {
for (int i = 1; i <= 7; i++)
parent[i] = i;
Union(3, 4); // p[4] = 3
Union(4, 5); // p[5] = 3
Union(5, 6); // p[6] = 3
Union(6, 7); // p[7] = 3
for (int i = 1; i <= 7; i++){
printf("%d ", parent[i]);
// 1 2 3 3 3 3 3
}
return 0;
}위 코드에 따르면, 4번, 5번, 6번, 7번 노드 모두 3번을 parent 배열의 값으로 갖는다. 이처럼 루트 노드 번호를 저장하면 트리의 치우침으로 인한 재귀 호출 반복 문제를 해결할 수 있다.

